Check the below NCERT MCQ Class 12 Mathematics Chapter 10 Vector Algebra with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Vector Algebra Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Vector Algebra Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 10 Vector Algebra with solutions. Solve questions and compare with the answers provided below
Question. ABC is a triangle and P is any point on BC such that P̅Q̅ is the resultant of the vectors A̅P̅ , P̅B̅ and P̅C̅ , then
(a) the position of Q depends on position of P
(b) Q is a fixed point
(c) Q lies on AB or AC
(d) None of these
Answer
B
Question. If the positive numbers a, b and c are the pth, qth and rth terms of GP, then the vectors log1

(a) equal
(b) parallel
(c) perpendicular
(d) None of these
Answer
C
Question. If|a|=|b||c|=1 and a·b = b ·c = cos θ, then the maximum value of θ is
(a) π/3
(b) π/2
(c) 2√/3
(d) 2π/5
Answer
C
Question. If a, b and c are coplanar vectors and λ is a real number, then the vectors a+ 2b+ 3c, λb +µc l and (2λ -1)c are coplanar for
(a) all values ofµ
(b) λ = 1/2
(c) λ = 0
(d) no value of
Answer
(A,B,D)
Question. If a is a unit vector and projection of x along a is 2 and ax r+ b= r, is equal to

Answer
B
Question. Let a ,b and c be three unit vectors such that a is perpendicular to the plane of b and c. If the angle between

(a) 1/3
(b) 1/2
(c)1
(d) 2
Answer
C
Question.

Answer
A
Question.

(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
Question.

Answer
D
Question. If A(-4,0, 3) and B(14,2,-5), then which one of the following points lie on the bisector of the angle between OA and OB(O is the origin of reference)?
(a) (2 ,2 ,4)
(b) (2,11,5)
(c) (-3,- 3,- 6)
(d) (1 1,2)
Answer
(A,C,D)
Question.

Answer
B
Question.

Answer
(A,B,D)
Question. a and b are two given vectors. With these vectors as adjacent sides, a parallelogram is constructed. The vector which is the altitude of the parallelogram and which is perpendicular to a is

Answer
(A,B,C)
Question. If three points A, B and C have position vectors (1, x, 3), (3, 4, 7) and (y, – 2, – 5) respectively and, if they are collinear, then (x – y) is equal to
(a) (2, – 3)
(b) (– 2, 3)
(c) (2, 3)
(d) (– 2, – 3)
Answer
A
Question.

(a) 3
(b) 0
(c) 1
(d) 2
Answer
A
Question. If a̅ = î + 2ĵ + 3k̂ , b̅ = 2î + 3ĵ + k̂ , c̅ = 3î + ĵ + 2k̂ and α a̅ + βb̅ + ϒc̅ = -3(î – k̂) , then the ordered triplet (α, β, ϒ) is
(a) (2, –1, –1)
(b) (–2, 1, 1)
(c) (–2, –1, 1)
(d) (2, 1, –1)
Answer
A
Question. A unit vector perpendicular to the plane formed by the points (1, 0, 1), (0, 2, 2) and (3, 3, 0) is
(a) 1/5√3 (5î – ĵ -7k̂)
(b) 1/5√3 (5î – ĵ + 7k̂)
(c) 1/5√3 (5î -+ ĵ + 7k̂)
(d) None of these
Answer
B
Question. A girls walks 4 km towards West. Then, she walks 3 km in a direction 30° East to North and stops. The girls displacement from her initial point of departure is
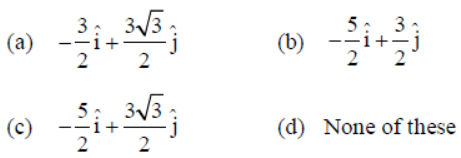
Answer
C
Question. ABCD is a parallelogram whose diagonals meet at P. If O is a fixed point, then O̅A̅ + O̅B̅ + O̅C̅ + O̅D̅ equals
(a) O̅P̅
(b) 2 O̅P̅
(c) 3 O̅P̅
(d) 4 O̅P̅
Answer
D
Question. If the vertices of any tetrahedron be A̅ = J̅ + 2K̅ , B̅ = 3I̅ + K̅ ,
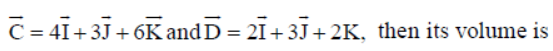
(a) 1/6 units
(b) 6 units
(c) 36 units
(d) None of these
Answer
B
Question. A vector whose magnitude is the same as that of a given vector, but direction is opposite to that of it, is called
(a) negative of the given vector
(b) equal vector
(c) null vector
(d) collinear vector
Answer
A
Question. a̅ , b̅ , c̅ are 3 vectors, such that a̅ + b̅ + c̅ = 0 , |a̅| = 1 , |b̅| = 2 , |c̅| = 3 , , then a̅.b̅ + b̅.c̅ + c̅.a̅ is equal to
(a) 1
(b) 0
(c) – 7
(d) 7
Answer
C
Question. Two or more vectors having the same initial point are called
(a) unit vectors
(b) zero vectors
(c) coinitial vectors
(d) collinear vectors
Answer
C
Question. The non-zero vectors are a̅ , b̅ and c̅ are related by a̅ = 8b̅ and c̅ = -7b̅ . Then the angle between a̅ and c̅ is
(a) 0
(b) π/4
(c) π/2
(d) π
Answer
D
Question. The vectors
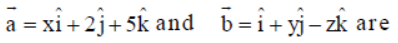
collinear, if
(a) x = 1, y = – 2, z = – 5
(b) x = 1/2, y = – 4, z = – 10
(c) x = – 1/2, y = 4, z = 10
(d) All of these
Answer
D
Question. If b̅ and c̅ are any two non-collinear mutually perpendicular unit vectors and a̅ is any vector, then
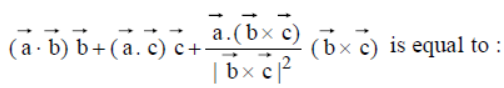
(a) a̅
(b) 2a̅
(c) 3a̅
(d) None
Answer
A
Question. The angle between the vectors a̅ + b̅ and a̅ – b̅ , where a̅ = (1, 1, 4) and b̅ = (1, –1, 4) is
(a) 90°
(b) 45°
(c) 30°
(d) 15°
Answer
A
Question. If (a̅ x b̅)2 + (a̅.b̅)2 = 676 and |b̅| = 2 , then |a̅| is equal to
(a) 13
(b) 26
(c) 39
(d) None of these
Answer
A
Question. If | a̅ + b̅ |= a̅ – b̅ | then the vectors a̅ and b̅ are adjacent sides of
(a) a rectangle
(b) a square
(c) a rhombus
(d) None of these
Answer
A
Question. For any vector a̅ , the value of
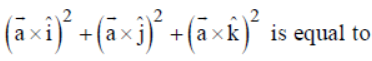
(a) a̅2
(b) 3a̅2
(c) 4a̅2
(d) 2a̅2
Answer
D
Question. If a girl moves from A to B and then from B to C (as shown). Then, net displacement made by the girl from A to C, is

(a) AB – BC = AC
(b) AC = AB – BC
(c) AC = AB + BC
(d) None of these
Answer
C
Question.
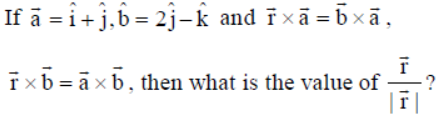

Answer
A
Question. A zero vector has
(a) any direction
(b) no direction
(c) many directions
(d) None of these
Answer
B
Question. If a̅ is any vector, then
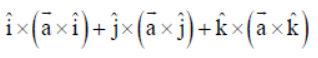
is equal to
(a) a̅
(b) 2a̅
(c) 3a̅
(d) 0
Answer
B
Question. A unit vector perpendicular to the plane ABC, where A, B and C are respectively the points (3, –1, 2), (1, –1, –3) and (4, –3, 1), is
(a) -1/√29 (2î + 5k̂)
(b) 1/√16(î – 2ĵ – k̂)
(c) 1/√26 (4î – 3ĵ +k̂)
(d) -1/√165 (10î + 7ĵ -4k̂)
Answer
D
Question.
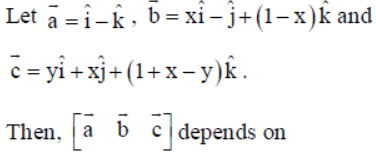
(a) neither x nor y
(b) both x and y
(c) only x
(d) only y
Answer
A
Question. If the scalar product of the vector î+ ĵ+ k̂ vector along the sum of vectors 2î + 4ĵ – 5k̂ and λî + 2ĵ + 3k̂is equal to one then the value of λ is
(a) 0
(b) – 1
(c) 1/2
(d) 1
Answer
D
Question. Magnitude of the vector joining the points P(x1, y1, z1) and Q(x2, y2, z2) is
(a) (x2 – x1) + (y2 – y1) + (z2 – z1)
(b) (x2 – y2 + z2) + (x1 + y1 + z1
(c) √(x2 – x1)2 + (y2 – y1)2
(d) None of the above
Answer
D
Question. Which of the following represents graphically the displacement of 40 km, 30° East of North?
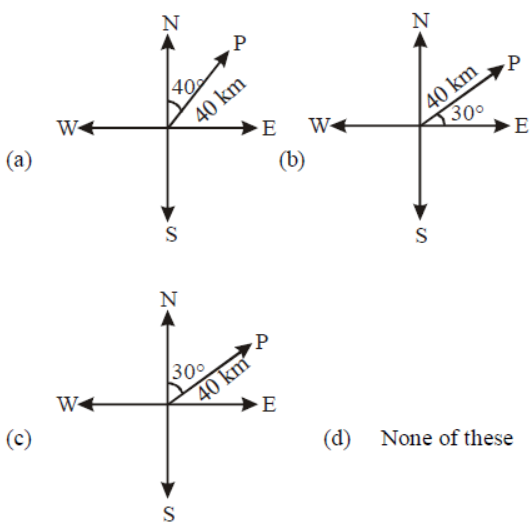
Answer
C
Question. Two vectors a̅ and b̅ are non-zero and non-collinear.
What is the value of x for which the vectors p̅ = ( x – 2) a̅ + b̅ and q̅ = (x + 1) a̅ – b̅ are collinear?
(a) 1
(b) 1/2
(c) 2/3
(d) 2
Answer
B
Question. If a̅ and b̅ are unit vectors inclined at an angle of 30° to each other, then which one of the following is correct ?

Answer
B
Question. Which of the following is/are true?
I. In a zero vector, initial and terminal points coincide.
II. Zero vector is denoted as O.
III. Zero vector has zero magnitude.
(a) Only II is true
(b) I and III are true
(c) II and III are true
(d) All are true
Answer
D
Question. The resultant moment of three forces î + 2ĵ – 3k̂ , 2î + 3ĵ + 4k̂ and -î – ĵ + k̂ acting on a particle at a point P (0, 1, 2) about the point A (1, –2, 0) is
(a) 6 √2
(b) √140
(c) √21
(d) None
Answer
B
Question. Which of the following is/are true?
I. To add two vectors a and b, they are positioned such that the initial point of one does not coincide with the terminal point of the other.
II. The resultant of the vectors AB and BC is represented by the third side AC of a triangle.
III. If sides of a triangle are taken in order, then it leads to zero resultant.
(a) Only I is true
(b) Only II is true
(c) II and III are true
(d) All are true
Answer
C
Question. If two vertices of a triangle are i – j and j + k, then the third vertex can be
(a) i + k
(b) i –2j – k and –2i – j
(c) i – k
(d) All the above
Answer
D
Question.
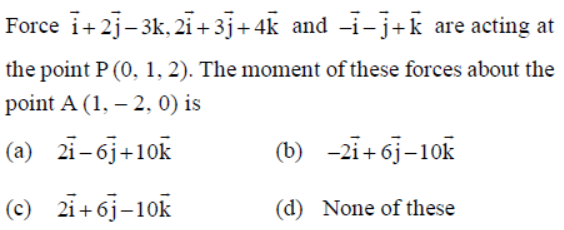
Answer
B
Question. If a̅ and b̅ are the two vectors such that a̅.b̅ = 0 and a̅ x b̅ = 0 , then
(a) a̅ is parallel to b̅ .
(b) a̅ is perpendicular to b̅ .
(c) either a̅ or b̅ is a null vector .
(d) None of these.
Answer
C
Question. The vector product of two non zero vector a and b, is denoted by a × b and is equal to
(a) |a| |b| cos θ
(b) a | | b sin θ n̅
(c) a | | b cos θ n̅
(d) None of these
Answer
B
Question. If | a̅ | = 5 , | b̅ | = 4 , | c̅ | = 3 , then the value of |a̅.b̅ + b̅.c̅ + c̅.a̅| , is equal to ( given that a̅ + b̅ + c̅ = 0 )
(a) 25
(b) 50
(c) –25
(d) –50
Answer
A
Question.

(a) 0
(b) 1
(c) – √3
(d) √3
Answer
A
Question. If |a̅| = 10 , |b̅| = 2 and a̅.b̅ = 12 , then the value of |a̅ x b̅| is
(a) 5
(b) 10
(c) 14
(d) 16
Answer
D
Question.

(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. If
are linearly dependent vectors and |c̅ | = √3 , then
(a) α = 1, β = – 1
(b) α = 1, β = ± 1
(c) α = – 1, β = ± 1
(d) α = β 1, ± = 1
Answer
D
Question. Which among the following figure correctly represents projection of AB on a line l ?
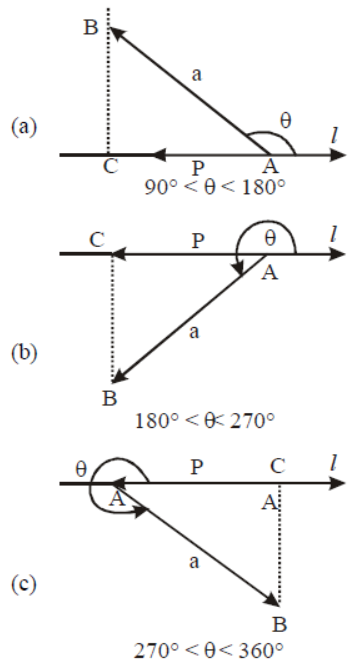
(d) All of these
Answer
D
Question. ABCDEF is a regular hexagon with centre at origin such that AD + EB + FC = λED, then λ is equal to
(a) 2
(b) 4
(c) 6
(d) 3
Answer
B
Question. The vector in the direction of the vector î – 2ĵ + 2k̂ that has magnitude 9 is
(a) î – 2ĵ + 2k̂
(b) î – 2ĵ + 2k̂/3
(c) 3(î – 2ĵ + 2k̂)
(d) 9(î – 2ĵ + 2k̂)
Answer
C
Question. In triangle ABC, which of the following is not true?
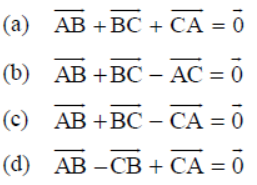
Answer
C
Question. If a̅ is a non-zero vector of magnitude a and l a non-zero scalar, then l a̅ is a unit vector if.
(a) l = 1
(b) l = – 1
(c) a = |l|
(d) a = 1/|λ|
Answer
D
Question. In the following table a̅ ≠ o̅ , b̅ ≠ o̅ and l1, m1, n1 and l2, m2, n2 are their d.c. and a1, b1, c1 and a2, b2, c2 are their d. r.s respectively.

Codes
A B C D E F
(a) 2 1 2 2 1 3
(b) 3 1 2 1 2 1
(c) 1 3 2 1 1 2
(d) 1 2 1 2 1 3
Answer
D
Question. For what value of m, are the points with position vector

(a) – 8
(b) 8
(c) 4
(d) – 4
Answer
B
Question. Let there be two points A, B on the curve y = x2 in the plane OXY satisfying O̅A̅ . î = 1 and O̅B̅ . î = -2 , then the length of the vector 2O̅A̅ – 3O̅B̅ is
(a) 14
(b) 2 √51
(c) 3 √41
(d) 2 √41
Answer
D
Question. Consider the figure given below
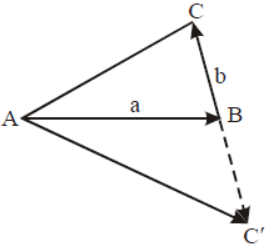
Here, it is shown that a vector BC’ is having same magnitude as the vector BC, but its direction is opposite to that of it.
Based on above information which of the following is true?
(a) AC’ = a + b
(b) AC’ = a – b
(c) Difference of a and b is AC
(d) None of these
Answer
B
Assertion – Reason Type Questions :
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion : If the point
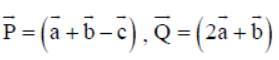

Reason : If P, Q, R are collinear, then

Answer
A
Question. Consider the shown figure.
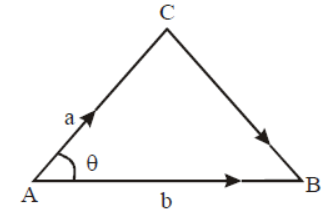
Assertion : If a and b represent the adjacent sides of a triangle as shown, then its area is 1/2|axb|
Reason : Area of ΔABC = 1/2|b||a| sin θ where, θ is the angle between the adjacent sides a and b (as shown).
Answer
A
Question. Assertion : In ΔABC , A̅B̅ + B̅C̅ + C̅A̅ = 0 .
Reason : If O̅A̅ = a̅, O̅B̅ = b̅ , then A̅B̅ = a̅+b̅ (triangle law of addition)
Answer
D
Question. Assertion : If I is the incentre of ΔABC , then |B̅C̅| I̅A̅ | C̅A̅ | I̅B̅ + |A̅B̅ | I̅C̅ = 0 .
Reason : The position vector of centroid of ΔABC is O̅A̅ + O̅B̅ + O̅C̅/3 .
Answer
C
Question. Assertion :

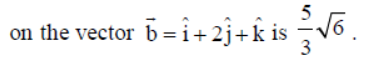
Reason : The projection of vector a on vector b is 1/|a| (a.b) .
Answer
C
