Please refer to the Class 11 Physics Sample Paper below. These CBSE Sample Papers for Class 11 Physics have been prepared based on the latest guidelines and examination patterns issued for the current academic year. We have provided Term 1 and Term 2 sample papers with solutions. You can click on the links below and access the free latest CBSE Sample Papers for Physics for Standard 11. All guess papers for Physics Class 11 have been prepared by expert teachers. You will be able to understand the type of questions which are expected to come in the examinations and get better marks.
CBSE Sample Papers for Class 11 Physics
| Term 2 Sample Papers |
| Class 11 Physics Sample Paper Term 2 With Solutions Set A |
Class 11 Physics Sample Paper Term 2 With Solutions Set A
SECTION – A
1. The bulk modulus of elasticity of solids, liquids and gases are Bs, Bl, Bg arrange them according to their magnitude.
Give reason.
Answer : Under constant stress, magnitude of bulk modulus of elasticity of material is inversely proportional to volumetric strain. B ∝ 1 / V/ΔV Since, gases has higher compressibility than liquid and solids have the least, therefore Bs > Bl > Bg.
2. When a stretched wire and a tuning fork are sounded together, 5 beats per second are produced, when length of wire is 95 cm or 100 cm, find frequency of the fork.
Answer : Let the frequency of tuning fork be n.
Suppose ∫1 = 95 cm has frequency n1 and ∫2 = 100 cm has frequency n2( < n1)
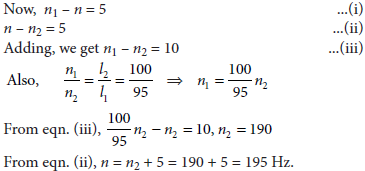
OR
From Doppler effect, beats, transverse waves and longitudinal waves which of the following does the intensity of sound vary with time?
Answer : Beats is the phenomenon of regular variation in the intensity of sound with time when two sources of nearly equal frequencies are sounded together. One minimum of sound followed by one maximum constitute one beat.
3. Refer to the plot of temperature versus time showing the changes in the state of ice on heating (not to scale).
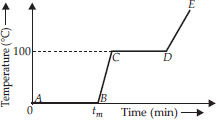
What represents AB in the given figure?
Answer : AB represents ice and water are not in the thermal equilibrium.
4. The time period of a simple pendulum is T. If the length of the pendulum is made 9 times and mass of the bob is made 4 times then find the value of time period.
Answer : The time period of the simple pendulum is
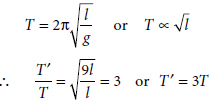
OR
A body of mass 500 g is attached to a horizontal spring of spring constant 8π2 N m–1. If the body is pulled to a distance of 10 cm from its mean position, then find its frequency of oscillation.
Answer :
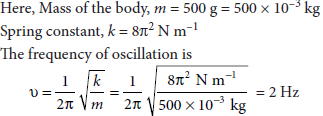
5. Why greenhouse are provided with glass roofs and glass doors?
Answer : Because glass is athermanous.
Assertion & Reason Question :
two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
6. Assertion (A) : The speed of sound in a gas is not affected by change in pressure provided the temperature of the gas remains constant.
Reason (R): The speed of sound is inversely proportional to the square root of the density of the gas.
Answer
B
7. Assertion (A): Coefficient of thermal conductivity of a metal rod is a function of length of the rod.
Reason (R): Longer the rod, larger is the amount of heat conducted.
Answer
D
SECTION – B
Case Study Based Question :
8. The appearance of sound to a human ear is characterised by three parameters (a) pitch (b) loudness and (c) quality. Pitch is related to frequency, loudness is related to intensity and quality is related to the waveform of the sound wave.
The pitch of a sound corresponds to frequency. Frequency is an objective property which can be assigned a unique value. However a person’s perception of frequency is subjective. The brain interprets frequency primarily in terms of a subjective quality called Pitch.
The loudness that we sense is related to the intensity of sound . The intensity of sound depends on pressure variations within the sound wave, it depends on the amplitude.
Sound “quality” or “timbre” describes those characteristics of sound which allows the ear to distinguish sounds which have the same pitch and loudness.
Intensity of sound waves :
Intensity of a wave is given by I = 1/2 pA2ω2v
Sound intensity in decibels :
Physiological sensation of loudness is closely related to the intensity of wave. There is a wide range of intensities that the human ear can detect. At frequency f = 1000 Hz, lowest audible intensity is 10–12 W/m2 and intensity of 1 W/m2 causes pain.
(i) If intensity of sound is increased by a factor of 1000, what will be increase in decibels?
(a) 30 dB
(b) 40 dB
(c) 50 dB
(d) 60 dB
Answer
A
(ii) The unit of sound is
(a) decible
(b) hertz
(c) meter
(d) meter2
Answer
B
(iii) At what temperature will the speed of sound be double its value at 0°C?
(a) 1090 K
(b) 1010 K
(c) 1082 K
(d) 1092 K
Answer
D
(iv) When sound wave is refracted from air to water which of the following quantities remains unchanged?
(a) Wavelength
(b) Wave number
(c) Wave velocity
(d) Frequency
Answer
D
(v) Out of the following gases under similar condition of temperature and pressure, the velocity of sound will be maximum in
(a) hydrogen
(b) nitrogen
(c) oxygen
(d) chlorine
Answer
A
SECTION – C
All questions are compulsory. In case of internal choices, attempt anyone.
9. A wire of length l and radius r has a weight W and the Young’s modulus of elasticity Y. It is suspended vertically from a fixed point. Calculate the increase in length of wire produced due to its own weight.
Answer : Since the tension is non-uniform along the wire, we have variable stress in wire. Let us consider a small element of length dx at a distance x from bottom end P as shown figure.

OR
The Young’s modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then what will be the ratio of the weights added to the steel and brass wires ?
Answer :
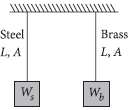
Let L and A be length and area of cross section of each wire. In order to have the lower ends of the wires to be at the same level (i.e. same elongation is produced in both wires), let weights Ws and Wb be added to steel and brass wires respectively. Then By definition of Young’s modulus, the elongation produced in the steel wire is
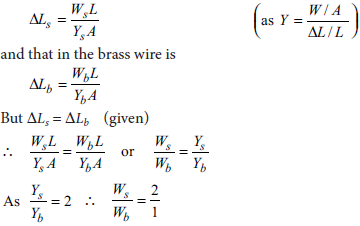
10. An ideal gas is expanding such that PT 2 = constant. Find the coefficient of volume expansion of the gas.
Answer :

11. A sample of 0.2 g of water at 100°C and normal pressure (1.013 × 105 N m–2) requires 54 cal of heat energy to convert to steam at 100°C. If the volume of the steam produced is 167.1 cc, find the change in internal energy of the sample.
Answer : Using first law of thermodynamics,
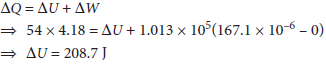
OR
At constant pressure heat is supplied to a diatomic gas. Find ratio of ΔQ : ΔU : ΔW.
Answer :
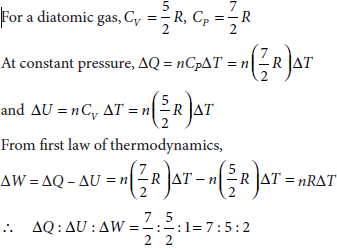
12. A gas has two specific heats whereas a liquid and a solid have only one. Why ?
Answer : When solids and liquids are heated, there is only a slight change in their volume and as such they possess only one specific heat, i.e., specific heat at constant volume. But in case of gases, pressure and volume both change and as such they possess two principal specific heats; one at constant pressure and one at constant volume.
SECTION – D
All questions are compulsory. In case of internal choices, attempt any one.
13. Two bodies are combined to form a single composite body having specific heats s1 and s2 What is the specific heat of the composite body?
Answer : Let m1 and m2 are the masses of two bodies. Heat capacity of the composite body
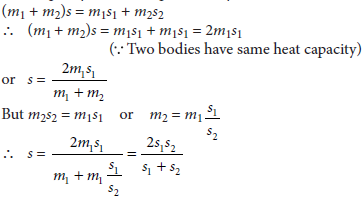
14. (a) State two conditions of a reversible process.
(b) What is the quasi-static process?
Answer : (a) : The process should take place very slowly, so that it satisfies the following conditions :
(i) The system should be in thermal equilibrium.
(i) The system should be in chemical equilibrium.
(b) A process in which the system passes through a continuous sequence of equilibrium states is said to be quasi-static process, i.e., apparently static.
OR
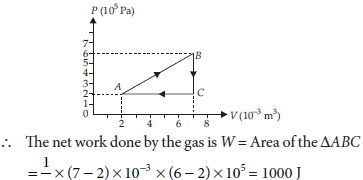
A gas is taken through the cycle A → B → C → A, as shown. What is the net work done by the gas?
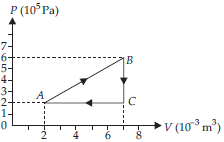
Answer : In a cyclic process, work done is equal to the area under the cycle and is positive if the cycle is clockwise and negative if the cycle is anticlockwise.
SECTION – E
All questions are compulsory. In case of internal choices, attempt any one.
15. (a) What is the phase difference between two simple harmonic motions represented by x1 = A sin {ωt + π/6} x2 = Acos(ωt)?
(b) The maximum velocity of particle, executing simple harmonic motion with an amplitude 7 mm, is 4.4 m s–1.
Find the time period of oscillation.
Answer :
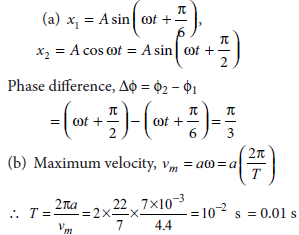
OR
(a) A particle executing a simple harmonic motion has a period of 6 sec. Find the time taken by the particle to move from the mean position to half the amplitude, starting from the mean position.
(b) The equation of SHM of a particle is given as 2 d2x/dt2 + 32x = 0 where x is the displacement from the mean position of rest. What is the period of its oscillation in seconds ?
Answer : (a) Since the motion is started from the mean position, therefore displacement x of a particle executing SHM at any time t from its mean position is given by
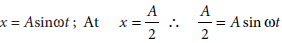

16. State and prove Bernoulli’s theorem.
Answer : Bernoulli’s principle : Bernoulli’s principle states that the sum of pressure energy, kinetic energy and potential energy per unit volume of an incompressible, non-viscous fluid in a streamlined irrotational flow remains constant along a streamline.
Mathematically, it can be expressed as
P + 1/2 pv2 + pgh = constant
Proof: Consider a non-viscous and incompressible fluid flowing steadily between the sections A and B of a pipe of varying cross-section. Let a1 be the area of cross-section at A, v1 the fluid velocity, P1 the fluid pressure, and h1 the mean height above the ground level. Let a2, v2, P2 and h2 be the values of the corresponding quantities at B.
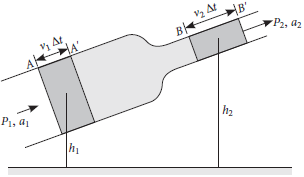
Let r be the density of the fluid. As the fluid is imcompressible, so whatever mass of fluid enters the pipe at section A in time Δt, an equal mass of fluid flows out at section B in time Δt. This mass is given by
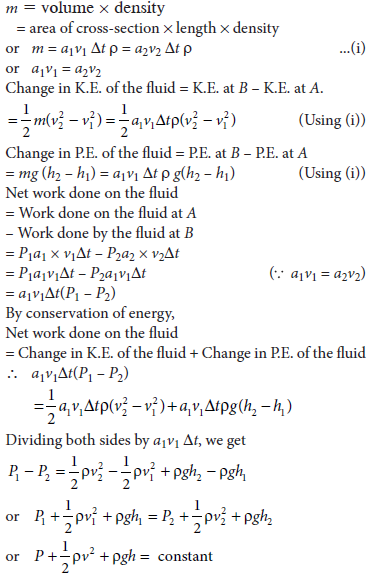
This proves Bernoulli’s principle according to which the total energy per unit volume remains constant.
OR
(a) State Pascal’s law of fluid pressure. Explain the working of hydraulic lift with suitable diagram.
(b) Why air bubbles in a liquid moves in upward direction?
Answer : (a) Pascal’s Law : If gravity effect is neglected the pressure in a fluid at rest is same at all points.
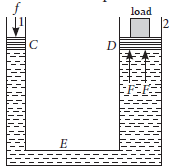
Hydraulic lift : It is used to lift the heavy loads. Its working is based on Pascal’s law. A simple hydraulic lift is shown in figure. Here C and D are two cylinders of different areas of cross-section. They are connected to each other with a pipe E. Each cylinder is provided with airtight frictionless piston. Let a, and A be the areas of crosssection of the pistons in C and D respectively, where a < < A. The cylinders are filled with an incompressible
liquid.
Let a downward force f be applied on the piston of C. Then the pressure exerted on the liquid, P = f/a. According to Pascal’s law, this pressure it transmitted equally to piston of cylinder D.
∴ Upward force acting on the piston of cylinder
D will be, F + PA + f/a A + f A/a
(b) The fluids move from higher pressure to lower pressure and a fluid pressure increases with depth. Hence pressure at the top is less than that at the bottom and so the air bubble will rise from bottom to top.



