Please refer to Quadrilaterals Class 9 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Mathematics Quadrilaterals Notes and Questions
A quadrilateral is a closed figure obtained by joining four point (with no three points collinear) in an order.
Every quadrilateral has : (i) Four vertices, (ii) Four sides, (iii) Four angles and (iv) Two diagonals.
SUM OF THE ANGLES OF A QUADRILATERAL
Statement: The sum of the angles ofa quadrilateral is 360°
TYPES OF QUADRILATERALS
1. Trapezium : It is quadrilateral in which one pair of opposite sides are parallel.
2. Parallelogram : It is a quadrilateral in which both the pairs of opposite sides are parallel.
3. Rectangle : It is a quadrilateral whose each angle is 90°. ABCD is a rectangle.
(i) ∠A+ ∠B = 90° + 90° = 180° ⇔ AD || BC
(ii) ∠B+ ∠C= 900 + 900 = 180° ⇔ AB || DC
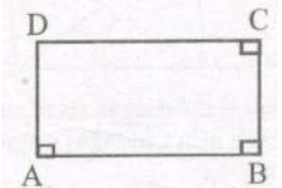
Rectangle ABCD is a parallelogram also.
4. Rhombus : It is a quadrilateral whose all the sides are equal.
5. Square : It is a quadrilateral whose all the sides are equal and each angle is 90°.
6. Kite : It is a quadrilateral in which two pairs of adjacent sides are equal.
Note :
• Square, rectangle and rhombus are all parallelograms.
• Kite and trapezium are not parallelograms.
• A square is a rectangle.
• A square is a rhombus.
• A parallelogram is a trapezium.
PARALLELOGRAM:
A parallelogram is a quadrilateral in which opposite sides are parallel. It is denoted by

PROPERTIES OF PARALLELOGRAM:
1. A diagonal of a parallelogram divides it into two congruent triangles.
2. The opposite sides of a parallelogram are equal.
Theorem : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
3. The opposite angles of a parallelogram are equal.
Theorem : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
4. The diagonals of a parallelogram bisect each other.
Theorem : If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
MID POINT THEOREM
(BASIC PROPORTIONALITY THEOREM)
Statement 1:
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side
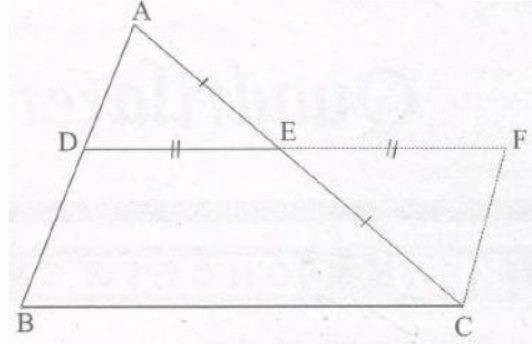
Statement 2:
The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
We hope the above Quadrilaterals Class 9 Mathematics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 9
