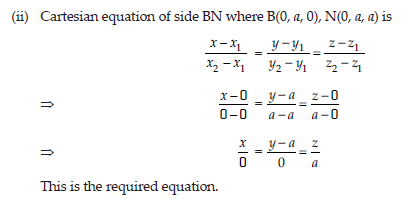Please refer to the Class 12 Mathematics Sample Paper below. These CBSE Sample Papers for Class 12 Mathematics have been prepared based on the latest guidelines and examination patterns issued for the current academic year. We have provided Term 1 and Term 2 sample papers with solutions. You can click on the links below and access the free latest CBSE Sample Papers for Mathematics for Standard 12. All guess papers for Mathematics Class 12 have been prepared by expert teachers. You will be able to understand the type of questions which are expected to come in the examinations and get better marks.
CBSE Sample Papers for Class 12 Mathematics
Class 12 Mathematics Sample Paper Term 2 With Solutions Set A
Section – A
1. Evaluate: ∫π/4-π/4 sin3 xdx.
OR
Evaluate: ∫2-2(x+2)dx
Answer:
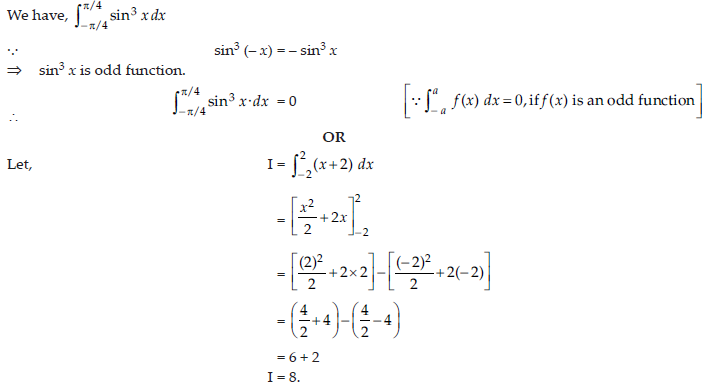
2. A refrigerator box contains 2 milk chocolates and 4 dark chocolates. Two chocolates are drawn at random.
Find the probability distribution of the number of milk chocolates. What is the most likely outcome?
Answer: Number of milk chocolates = 2
Number of dark chocolates = 4
Number of chocolate drawn = 2
Let X be the random variable representing no. of milk chocolates drawn, then x can be 0, 1, 2.
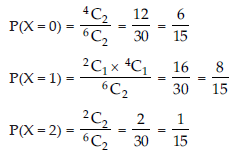

3. Find the distance between the two planes 2x + 3y + 4z = 4 and 4x + 6y + 8z = 16.
Answer: Given planes are,
2x+3y+4z=4
and 4x+6y+8z=16 …(1)
OR
2x + 3y + 4z = 8 …(2)
From the above equations, it can be seen that given planes are parallel.
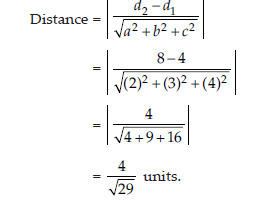
4. Find the sum of order and degree of the differential equation:
(d4y/dx4)2=[x+(dy/dx)2]3
Answer: Since,
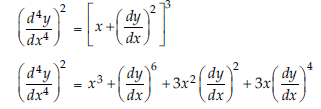
The equation represents a fourth order differential equation.
The highest power raised to d4y/dx4 is 2.
Hence, degree of the differential equation is 2.
So, the sum of order and degree of differential equation is = 4 + 2= 6.
5. Ram can find a solution of 60% of the problems given in mathematics examination paper and Shyam can find out 80% of it. What is the probability that atleast one of them will solve the problem that is selected at random?
Answer: Let us consider the events:
A = Ram finds the solution
B = Shyam finds the solution
Since, A and B are independent events.
So
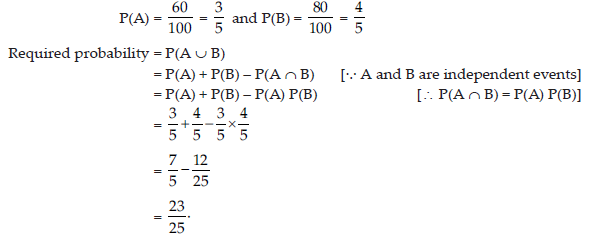
6. Find the magnitude of each of the two vectors a →and b→, having the same magnitude such that the angle between them is 60° and their scalar product is 9/2·
Answer:
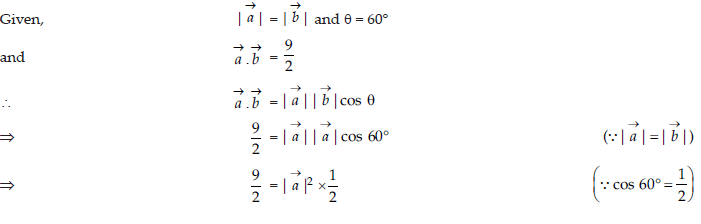
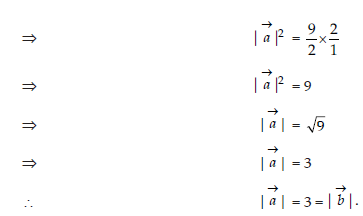
Section – B
7. If →a= î+ ĵ +k̂,→ b= 2 î -ĵ +3 k̂ and→ cî-2 ĵ + k
find a unit vector parallel to the vector 2 →a- →b +3→ c.
Answer:
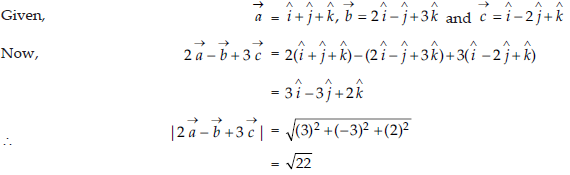
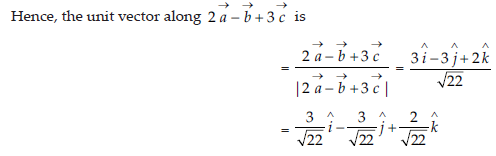
8. Find the vector equation of the plane which passes through the point (5, 2, – 4) and perpendicular to the line with direction ratios 2, 3, – 1.
OR
From the point P(1, 2, 4), a perpendicular is drawn on the plane 2x + y – 2z + 3 = 0. Find the equation, the length and co-ordinates of the foot of the perpendicular.
Answer:

OR
Draw PM perpendicular upon the given plane.
Equation of the line PM through P(1, 2, 4) and perpendicular to the plane 2x + y – 2z + 3 = 0 is,


9. Evaluate: ∫sin6x+ cos6 x/sin2x.cos2xdx.
Answer:

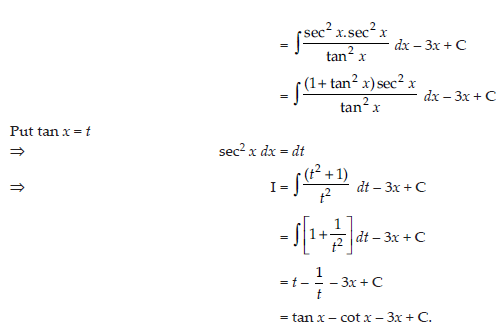
10. Solve the following differential equation:
(x2 – 1) dy/dx+ 2xy =1/x2 − 1: |x|≠ 1
OR
Solve the following differential equation:
(x2+1 )dy/dx+ 2xy= √x2+4
Answer: Given differential equation is

OR
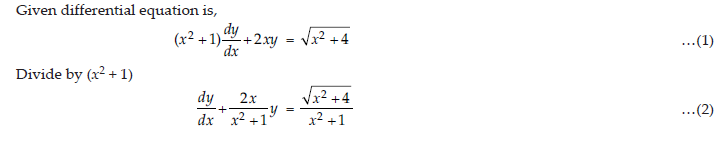

Section – C
11. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and found to be both clubs. Find the probability of the lost card being a club.
Answer: Let, E1 be the event that the lost card is club.
Let, E2 be the event that the lost card is not club.
Let, A be the event that both two cards drawn are clubs.
Then,
p(E1)=13/52=1/4,P(E2)=39/52=3/4
When one card is lost, number of remaining cards in the pack = 51.
When E1 has occured i.e., a card of clubs is lost, then the probability of drawing 2 cards of clubs from the remaining pack.
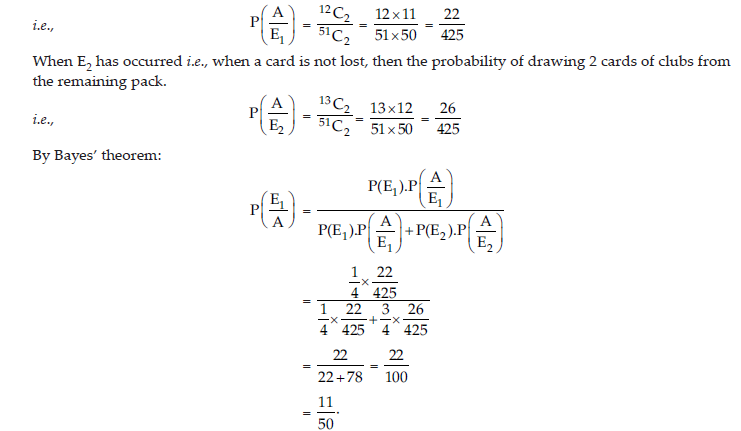
12. Find the area of the region bounded by the curves x2 + y2 = 4, y = √3x and x-axis in the first quadrant.
OR
Find the area of ellipse x2 + 9y2 = 36 using integration.
Answer:

OR

13. Evaluate: ∫2x+ 5/√7-6x-x2 dx.
Answer:
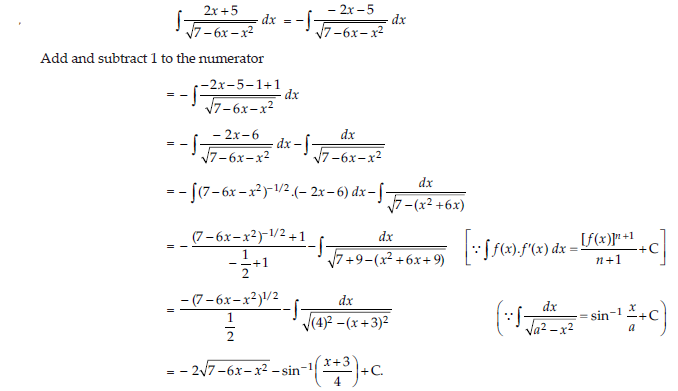
14. A badminton hall is to be constructed in the form of a cube in a sports complex in 3-D as given
below :
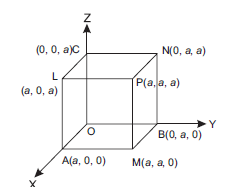
Length of side of cube be ‘a’ units, four diagonals are OP, MC, AN and BL.
From the above information given, answer the following questions :
(i) Find the direction cosines of diagonal AN.
(ii) Write the cartesian equation of the side BN.
Answer: