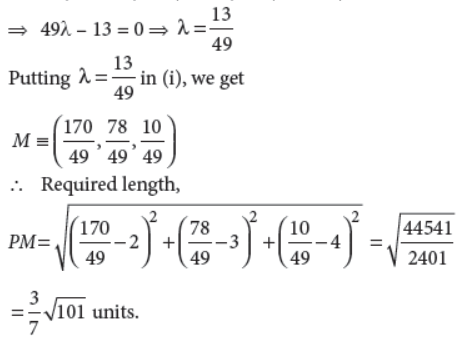Please refer to Class 12 Mathematics Sample Paper With Solutions Set B provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
PART – A
Section – I
1. Solve the differential equation sin (dy/dx) = a.
Answer :
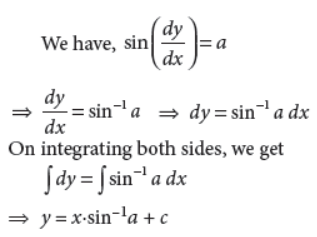
OR
Solve the differential equation
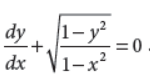
Answer :
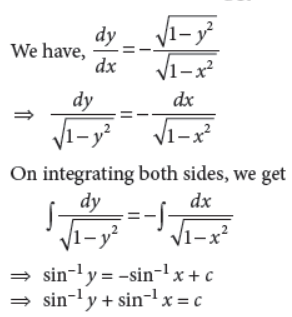
2. Check whether the function f : z → z, defined by f(x) = x2 + 5 ∀x ∈ z is one-one or not.
Answer : Since, f(1) = f(–1) = 6, therefore f is not one-one.
[ For f to be one-one distinct elements
should have distinct imaγes]
3. A line makes angles α, β and γ with the coordinate axes. If α + β = 90°, then find the value of angle γ.
Answer : We know that cos2α + cos2β + cos2γ = 1
⇒ cos2α + cos2(90° – α) + cos2γ = 1 [∵ α + β = 90°]
⇒ cos2α + sin2α + cos2γ = 1 ⇒ 1 + cos2γ = 1
⇒ cos2γ = 0 ⇒ cosγ = 0 ⇒ γ = 90°.
OR
Find the distance of the plane 5x – y + 6z – 12 = 0 from the origin.
Answer : Required distance =
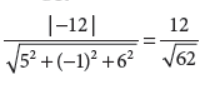
4. If
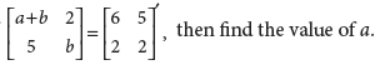
Answer :
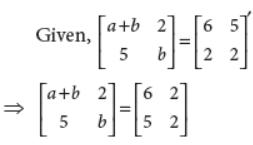
On comparing corresponding elements of the matrices,
we get a + b = 6 and b = 2 ⇒ a = 4
5. If |a̅| −|b̅| = |a̅| = |b̅|=1, then find the angle between a̅ and b̅.
Answer : Given |a̅| −|b̅| = |a̅| = |b̅|=1
Now |a̅−b̅|2 = |a̅|2 + |b̅|2 –2a̅b̅ ⇒ 1=1+1−2|a̅|.|b̅| cosθ (where θ is angle between a̅ and b̅)
⇒ cosθ = 1/2 ⇒ θ = π/3
OR
Find the magnitude of each of the two vectors a̅ and b̅ , having the same magnitude such that the angle between them is 60° and their scalar product is 9/2.
Answer :
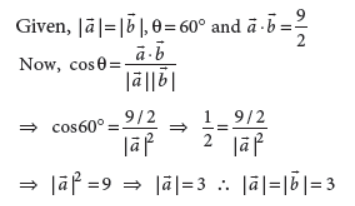
6. Let A = {1, 2, 3}. Check whether the relation {(1,1),(2,2),(3,3),(1,2),(2,1)} is an equivalence relation on A or not.
Answer : We have, A = {1, 2, 3}
and let R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
Since, for each a ∈ A, we have (a, a) ∈ R.
Also, (a, b) ∈ R ⇒ (b, a) ∈ R
and (1, 2) ∈ R, (2, 1) ∈ R ⇒ (1, 1) ∈ R
Thus, R is reflexive, symmetric and transitive .
Hence, R is an equivalence relation.
7. Evaluate :
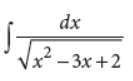
Answer :
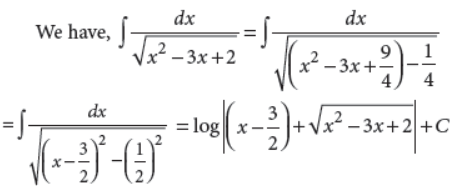
OR
Evaluate :
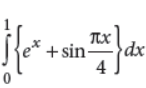
Answer :
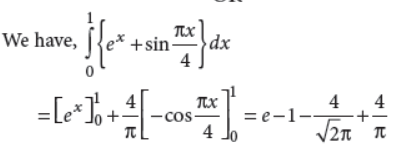
8. Find the area of the shaded region, shown in the given figure.
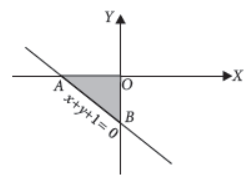
Answer :
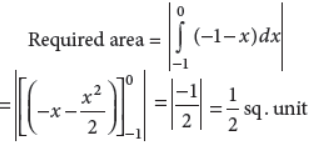
9. A bag contains 12 balls, of which 5 are red and 7 are blue. If 2 balls are drawn at random then find the probability of getting atleast 1 blue ball.
Answer : Required probability = 1 – P (getting no blue ball)
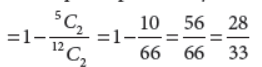
OR
If A and B are two independent events such that P(B) ≠ 0, then find P(A | B).
Answer :
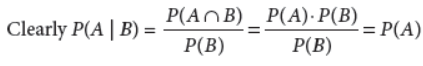
10. If A and B are symmetric matrices of the same order, then show that AB + BA is a symmetric matrix.
Answer :
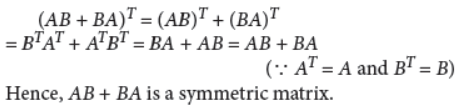
11. The probability distribution of a random variable X is given below :
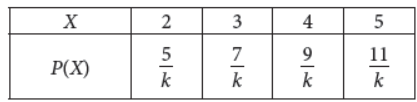
Find the value of k.
Answer : Clearly, ∑P(X) = 1
12. If the equation of a line is 2x–5/4 = y+4/3 = 6–z/6 , then find the direction cosines of a line parallel to this line.
Answer :

13. If P(not E) = 0.36 and P(F | E) = 0.5, then find P(E ∩ F).
Answer : Clearly, P(E) = 1 – P( E ) = 1 – 0.36 = 0.64
Now, P(F | E) = 0.5
⇒ P(E∩F) /P(E) = 0.5 ⇒ P(E∩F) = P(E) x 0.5
= 0.64 × 0.5 = 0.32
14. Check whether the following arrow diagram represents a function or not.
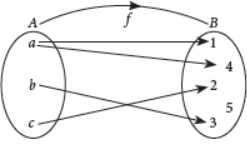
Answer : As f(a) is not unique, therefore f is not a function.
15. If A and B are two independent events, then show that the probability of occurrence of atleast one of A and B is given by 1 – P(A′) P(B′).
Answer : P(atleast one of A and B)
= P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) P(B) [∵ A, B are independent]
= P(A) + P(B) [1 – P(A)] = [1 – P(A′)] + P(B) P(A′)
= 1 – P(A′) + P(B) P(A′) = 1 – P(A′) [1 – P(B)]
= 1 – P(A′) P(B′)
16. The value of the determinant of a matrix A of order 3 × 3 is 4. Find the value of |5A|.
Answer : Given, A is a 3 × 3 matrix and |A| = 4
⇒ |5A| = 53 ⋅ |A| = 125 × 4 = 500.
Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. Two cars A and B are running at the speed more than allowed speed on the road along the lines r̅ = î + ĵ − k̂ + λ(3î − ĵ) and r̅ = 4î − k̂+ μ(2i + 3k), respectively.
Based on the above answer the following :
(i) The cartesian equation of the line along which car A is running, is

Answer : B
(ii) The direction cosines of line along which car A is running, are
(a) 3, –1, 0
(b) – 3, –1, 0
(c) 3/√10 ,−1/√10 , 0
(d) −3/√10 ,−1/√10 , 0
Answer : C
(iii) The direction ratios of line along which car B is running, are
(a) 3, 0, 2
(b) 2, 3, 0
(c) 2, 0, 3
(d) 0, 3, 2
Answer : C
(iv) The shortest distance between the gives lines is
(a) 4 units
(b) 2√3 units
(c) 3√2 units
(d) 0 units
Answer : D
(v) The cars will meet with an accident at the point
(a) (–1, 0, 4)
(b) (4, 0, –1)
(c) (4, –1, 0)
(d) does not exist
Answer : B
18. Neeta has a rectangular painting having a total area of 24 ft2 which includes a border of 1 ft on the left, right, bottom and a border of 2 ft on the top inside it.
Based on the above information, answer the following questions :
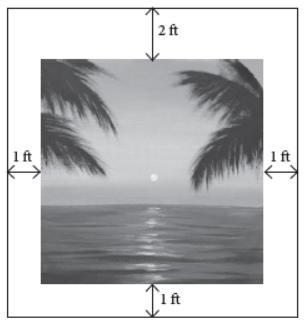
(i) If Neeta wants to paint in the maximum area, then she needs to maximize
(a) Area of outer rectangle
(b) Area of inner rectangle
(c) Area of top border
(d) None of these
Answer : B
(ii) It x is the length of the outer rectangle, then area of inner rectangle in terms of x is
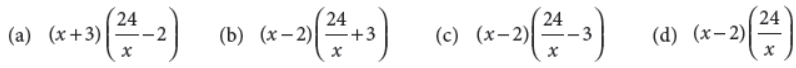
Answer : C
(iii) Find the range of x.
(a) (2, ∞)
(b) (2, 8)
(c) (– ∞, 2)
(d) (–2, 8)
Answer : B
(iv) If area of inner rectangle is maximum, then x is equal to
(a) 2 ft
(b) 3 ft
(c) 4 ft
(d) 5 ft
Answer : C
(v) If area of inner rectangle is maximum, then length and breadth of this rectangle are respectively
(a) 2 ft, 3 ft
(b) 3 ft, 4 ft
(c) 1 ft, 2 ft
(d) 2 ft, 4 ft
Answer : A
PART – B
Section – III
19. If P(A) = 3/8, P(B) = 1/2 and P(A∩B) = 1/4 ,then find P(A̅|B̅) and P(B̅|A̅).
Answer : We hA̅ve, P(A̅∩B̅) = P(A̅∪B̅)
⇒ P(A̅∩B̅) = 1− P(A̅∪B̅)
⇒ P(A̅∩B̅) = 1−{P(A̅)+ P(B̅) − P(A̅∩B̅)}
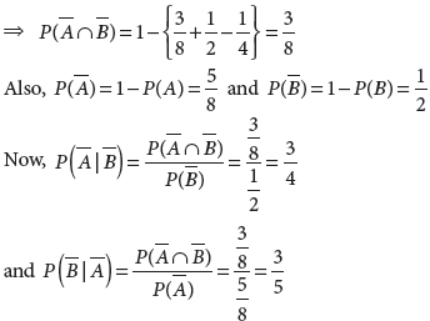
20. Evaluate :
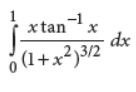
Answer : Let tan–1 x = θ ⇒ x = tan θ ⇒ dx = sec2 θ dq
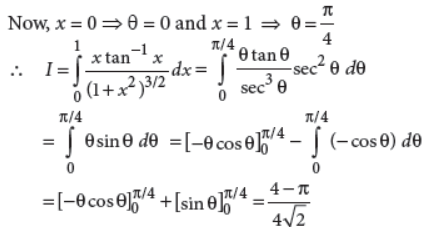
OR
Evaluate :
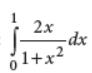
Answer :
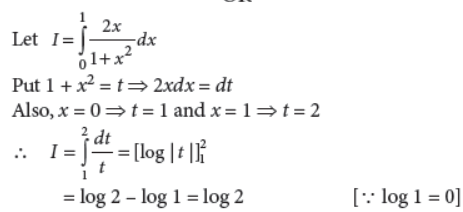
21. Find the equation of the normal to the curve y = x2 + 4x + 1 at the point where x = 3.
Answer : When x = 3, we have y = (32 + 4 × 3 + 1) = 22
So, the point of contact is (3, 22)
Now, y = x2 + 4x + 1
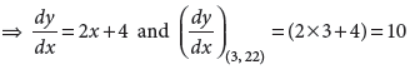
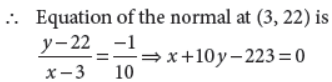
22. Find a matrix A such that 2A – 3B + 5C = O, where
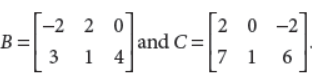
Answer : Given, 2A – 3B + 5C = O
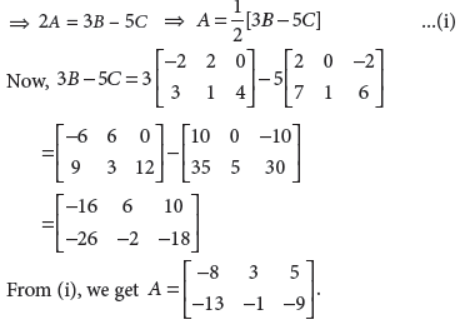
23. If a̅ + b̅ + c̅ = 0, then prove tha̅t a̅ ×b̅ = b̅ × c̅ = c̅ × a̅ .
Answer :
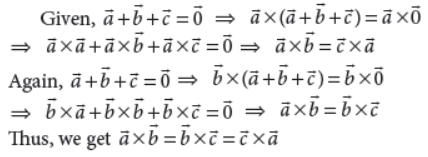
OR
If the angle between î + ĵ + ak̂ and î + k̂ is π/3, then find the values of a.
Answer :
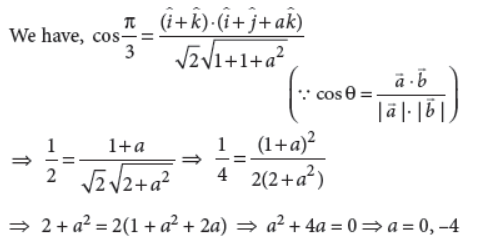
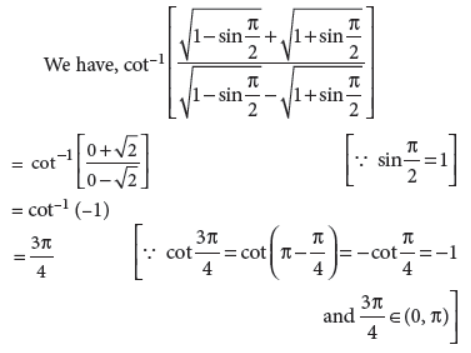
24. Find the principal value of
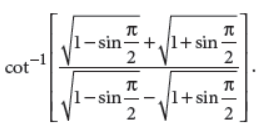
Answer :
25. Let X and Y be two events such that P(X) = 1/3 ,P(Y) = 4/15 and P(Y | X) = 2/5.Then find P(X’|Y).
Answer :
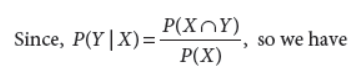
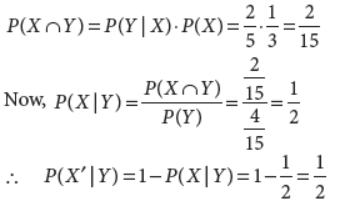
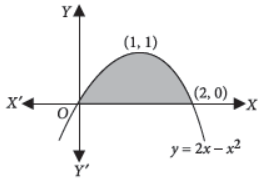
26. Find the area bounded by the parabola y = 2x – x2 and x-axis.
Answer : The bounded region is as shown in figure. Curve is y = 2x – x2 ⇒ y – 1 = –(x – 1)2 is a downward parabola with vertex (1, 1)
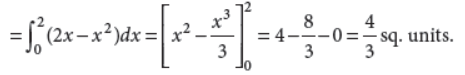
27. Determine the constants a and b such that the function
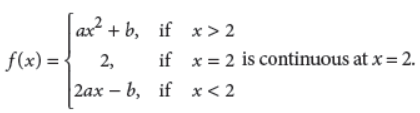
Answer : We have, R.H.L. (at x = 2)
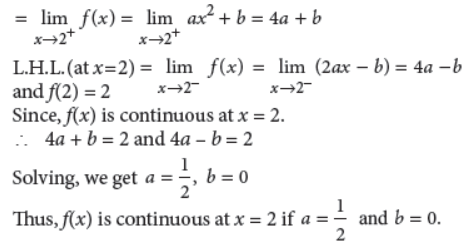
28. Solve the differential equation (x–1)dy/dx = 2xy.
Answer :
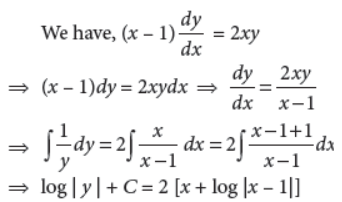
OR
Solve the differential equation 5 dy/dx = exy4.
Answer :
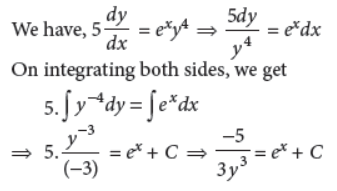
Section – IV
29. Evaluate :
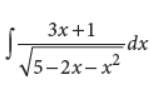
Answer :
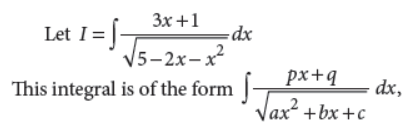
where px + q is given by
px + q A d/dx (ax2 + bx + c)+ B
Now, we write given integrand as
3x + 1 A d/dx (5–2X–X2)+B
⇒ 3x + 1 = A( – 2 –2x) + B
⇒ 3x + 1 = – 2Ax + (–2A + B)
On equating the coefficients of x and constant term both sides, we get

30. Show that the function f (x) = |x – 3|, x ∈ R is continuous but not differentiable at x = 3.
Answer : Given, f (x) = |x – 3|, x ∈ R.
∴ f (3) = |3 – 3| = |0| = 0
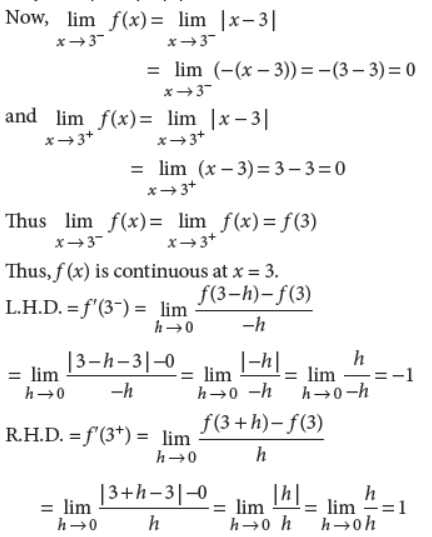
⇒ L.H.D. ≠ R.H.D.
Thus, f (x) is not differentiable at x = 3.
31. Find the solution of the differential equation (x2 – 2x + 2y) dx + x dy = 0.
Answer :

OR
Solve : ex√(1-y2)dx+y/x dy =0.
Answer :

32. Find the area lying in the first quadrant bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2.
Answer : Required area
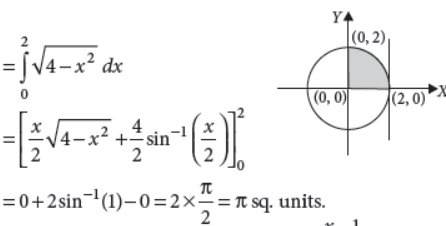
33. Let A = R – {2} and B = R – {1}. If f : A → B is a function defined by, f(x) = x–1/x–2 , show that f is one-one and onto.
Answer :
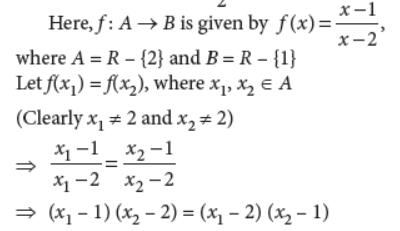
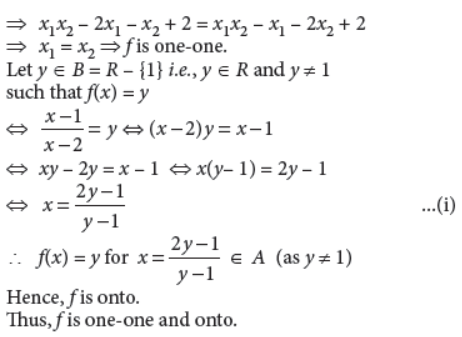
34. Find the derivative of the function
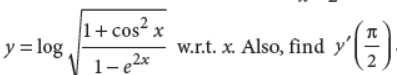
Answer :
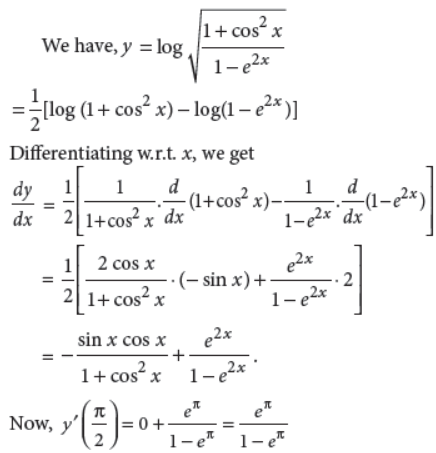
OR
If f(x) = [x], – 2 ≤ x ≤ 2, then show that f(x) is neither continuous nor differentiable at x = 1.
Answer :

35. Find the minimum value of the function f (x) = x logx.
Answer : We have, f (x) = x log x
∴f ′ (x) = 1 + log x and f”(x) = 1/X
Now f ′ (x) = 0, if 1 + log x = 0
⇒ log x = – 1 = – log e
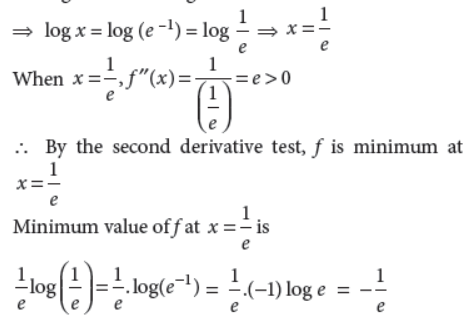
Section – V
36. Using concept of inverse of matrix, find the matrix A satisfying the matrix equation
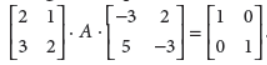
Answer :

OR
Using A–1, solve the following system of equations :
2x – 3y + 5z = 11
3x + 2y – 4z = –5
x + y – 2z = –3
Answer :
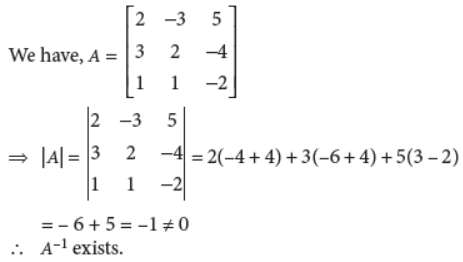
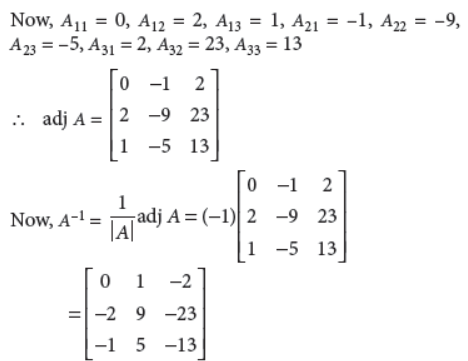
The given system of equations is
2x – 3y + 5z = 11, 3x + 2y – 4z = –5, x + y – 2z = –3
This system of equations can be written as AX = B,
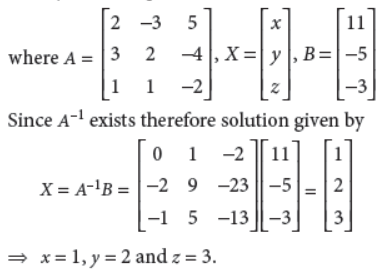
37. Solve the following LPP graphically.
Maximize Z = 2x/25 + y/10
Subject to constraints
x ≥ 2000, y ≥ 4000
and x + y ≤ 12000
Answer : Given L.P.P. is Maximize Z= 2X/25 + Y/10 ……..(1)
subject to constraints
x ≥ 2000 … (ii)
y ≥ 4000 … (iii)
and x + y ≤ 12000 … (iv)
On plotting inequalities (ii), (iii) and (iv), we get the
shaded region, which is bounded in the following figure.
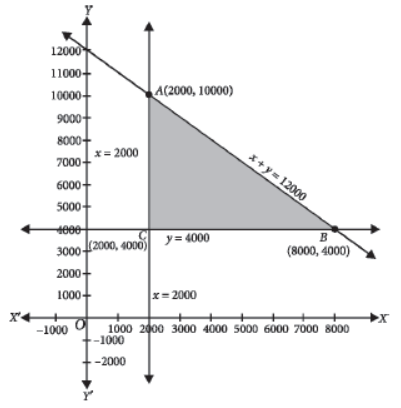
Now, we evaluate Z at the corner points
A(2000, 10000), B(8000, 4000) and C(2000, 4000).
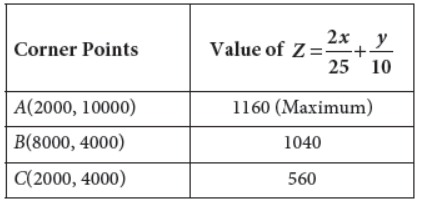
Clearly, maximum value of Z is 1160 at x = 2000 and y = 10000.
OR
Solve the following problem graphically.
Minimize Z = x – 7y + 190
subject to constraints
x + y ≤ 8
x + y ≥ 4
x ≤ 5
y ≤ 5
and x ≥ 0, y ≥ 0
Answer : The given problem is Minimize Z = x – 7y + 190
subject to x + y ≤ 8, x + y ≥ 4, x ≤ 5, y ≤ 5 and x ≥ 0, y ≥ 0
To solve this LPP graphically, let us first covert the inequations into equations and draw the corresponding lines.
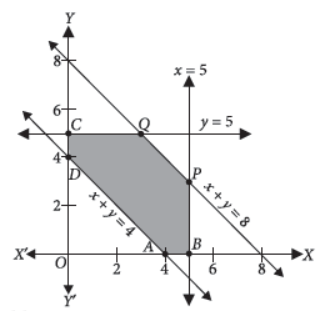
The feasible regions ABPQCDA.
P is the point of intersection of x = 5 and x + y = 8
i.e., P(5, 3) and Q is the point of intersection of y = 5 and x + y = 8 i.e., Q(3, 5).
The corner points of the feasible region are A(4, 0),
B(5, 0), P(5, 3), Q(3, 5), C(0, 5) and D(0, 4).
The value of the objective function Z = x – 7y + 190 at these points are
Z(A) = 4 – 7(0) + 190 = 194
Z(B) = 5 – 7(0) + 190 = 195
Z(P) = 5 – 7(3) + 190 = 174
Z(Q) = 3 – 7(5) + 190 = 158
Z(C) = 0 – 7(5) + 190 = 155
Z(D) = 0 – 7(4) + 190 = 162
Clearly, Z is minimum at x = 0, y = 5. The minimum value of Z is 155.
38. Find the vector equations of the planes through the intersection of the planes r̅ = (2î + 6ĵ) +12 = 0 andr̅ = (3î – 6ĵ + 4k̂) = 0 , which are at a unit distance from the origin.
Answer : The equation of the planes through the intersection of the planes
r̅. (2î + 6ĵ) + 12 = 0 and
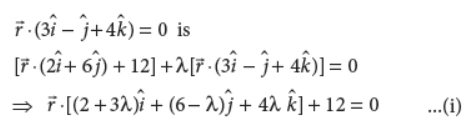
These planes are at a unit distance from the origin.
Therefore, length of the perpendicular from the origin on (i) is 1 unit.

OR
Find the coordinates of the foot of the perpendicular drawn from the point (2, 3, 4) to the line 4–x/2 = y/6 = 1–z/3 , Also, find the perpendicular distance from the given point to the line.
Answer : Let M be the foot of the perpendicular drawn from the point P(2, 3, 4) to the given line.
The coordinates of any point on the line
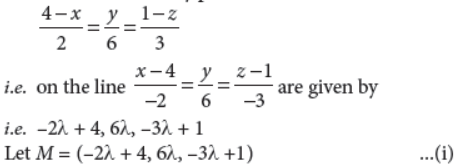
∴ Direction ratios of PM are –2λ + 2, 6λ – 3, –3λ – 3
The direction ratios of the given Line are –2, 6, –3
Since PM is perpendicuLar to the given Line
∴–2(–2λ + 2) + 6(6λ – 3) – 3(–3λ – 3) = 0