Class 12 Mathematics Sample Paper With Solutions Set J

Please refer to Class 12 Mathematics Sample Paper With Solutions Set J provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.

SECTION – A

1. Find the value of tan⁻¹√3 − cot⁻¹(−√3) .
Sol. tan⁻¹√3 − cot⁻¹(−√3) = tan⁻¹ tan π/3 − cot⁻¹ cot 5π/6 = π/3 − 5π/6 = − 3π/6 = −π/2

2. 

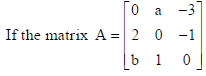
is skew symmetric, find the value of ‘a’ and ‘b’.
Sol. As A is skew symmetric so, A = −A^T i.e., a_ij = −a_ji if A = [a_ij] .
Therefore, a₁₂ = −a₂₁    ⇒ a = −2 and, a₃₁ = −a₁₃       ⇒b = −(−3) = 3 .

3. Find the magnitude of each of the two vectors a̅ and b̅, having same magnitude such that the angle between them is 60^o and their scalar product is 9/2 .
Sol. Sol. as a̅ .b̅ = |a̅||b̅| cosθ      ⇒ 9/2 = |a̅||a̅| cos60^o   ⇒ 9/2 = |a̅|² ×1/2    ∴ |a̅|= 3    Hence |a̅| = |b̅| = 3

4. If a * b denotes the larger of ‘a’ and ‘b’ and if a o b = (a *b) + 3, then write the value of (5) o (10), where * and o are binary operations.
Sol. (5) o (10) = (5*10) + 3 =10+ 3 =13 .

SECTION – B

5. Prove that : 

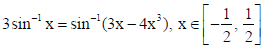
Sol. 

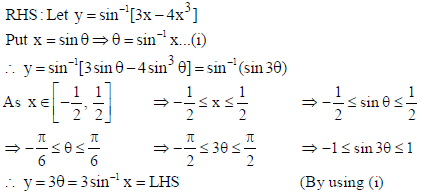
6. 

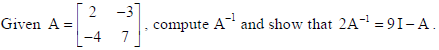
Sol.

7. Differentiate  

Sol.  

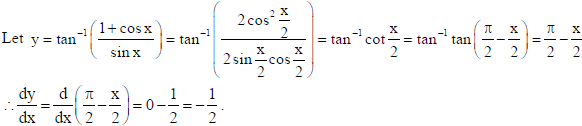
8. The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x³ − 0.02x² + 30x + 5000 . Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Sol. Given C(x) = 0.005x³ − 0.02x² + 30x + 5000     ⇒ d/dx [C(x)] = 0.015x² − 0.04x + 30 C'(x)
∴ C'(3) = 0.015×9− 0.04×3+ 30 = 30.015 .

9. Evaluate

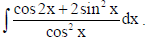
Sol. 

10. Find the differential equation representing the family of curves y = a ebx+5 , where a and b are arbitrary constants.
Sol. Given that y = a e^bx+5 …(i)
∴  dy/dx = ab e^bx+5 = yb       (By (i)
⇒ y’/y = b      ⇒ yy” − y’.y’/y² = 0     ⇒ yy’ − (y’)² = 0
Hence the required differential equation is y d²y/dx² − (dy/dx)² = 0.

11. If θ is the angle between two vectors î − 2ĵ+ 3k̂ and 3î − 2ĵ+ k̂ , find sin θ.
Sol. Let a̅ = î − 2ĵ+ 3k̂ and b̅ = 3î − 2ĵ+ k̂

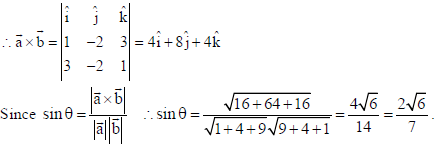
12. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Sol. Let E : sum of numbers appearing on the die is 8, F : the red die shows a number less than 4.

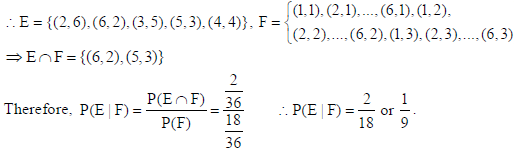
SECTION – C

13. Using properties of determinants, prove that

Sol. 

⇒ Δ = 9{0 + x +(y + z) + (1+ 3x)(yz − 0)}
⇒ Δ = 9{3xyz + xy + yz + zx} =RHS.

14. If (x² + y² )² = xy, find dy/dx. 
Sol. Here (x² + y²)² = xy                ⇒ 2(x² + y²){2x + 2yy’} = xy’ + y.1
⇒ 4(x² + y² ){x + yy’} = xy’ + y     ⇒ 4x(x² + y²) + 4y(x² + y² )y’ = xy’ + y
⇒ {4y(x² + y²) − x}y’ = y − 4x(x² + y²)

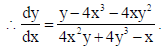
OR

If x = a(2θ − sin 2θ) and y = a(1−cos 2θ ), find dy/dx when  θ = π/3 
Sol. We have x = a(2θ −sin 2θ) and y = a(1− cos 2θ)

15. If y = sin(sin x) , prove that

Sol. 

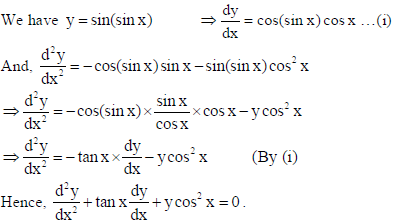
16. Find the equations of the tangent and the normal to the curve 16x² + 9y² =145 at the point (x₁ , y₁) , where x₁ = 2 and y₁ > 0.
Sol. Let P (x₁ , y₁) where x₁ = 2 and y₁ > 0.
Given curve is 16x² + 9y² =145 …(i)
Clearly P shall satisfy (i) so, 64 + 9y²₁ =145     ⇒ y₁ = 3 (as y > 0
Therefore, point of contact is P(2, 3).

OR

Find the intervals in which the function f (x) = x⁴/4 − x³ − 5x² + 24x + 12 is (a) strictly  increasing, (b) strictly decreasing.
Sol. 

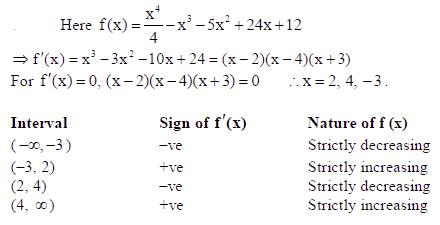
17. An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of the tank is half of its width. If the cost is to be borne by nearby settled lower income families, for whom water will be provided, what kind of value is hidden in this question?
Sol. Let length and width of the base of the open box be x and its depth be y. Also let volume of box

18. Find

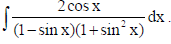
Sol. 

19. Find the particular solution of the differential equation e^x tan ydx + (2 − e^x )sec² ydy = 0 , given that y = π/4 when x = 0.
Sol.

OR

Find the particular solution of the differential equation dy/dx + 2y tan x = sin x, given
that y = 0  when x = π/4 
Sol. We have dy/dx + 2y tan x = sin x
⇒ dy/dx + (2 tan x)y = sin x
This differential equation is of the form dy/dx + P(x)y = Q(x), where P(x) = 2 tan x, Q(x) = sin x
So, integrating factor, I.F. = e^{∫2tan xdx} = e^{2logsec x} = sec² x
So, the solution is : ysec² x = ∫sec² x sin xdx + c       ⇒ ysec² x = ∫sec x tan xdx + c = sec x + c
Given that y=0 when x = π/3 so, 0 × sec² π/3 = sec π/3 + c = −2
Hence the required solution is ysec² x = sec x − 2 or, y = cos x − 2cos² x .

20. Let a̅ = 4î + 5ĵ− k̂, b̅ = î − 4ĵ+ 5k̂ and c̅ = 3î + ĵ− k̂ . Find a̅ vector d̅ which is perpendicular to both c̅ and b̅  and d̅.a̅ = 21
Sol. 

21. Find the shortest distance between the lines r̅ = (4î − ĵ) + λ(î + 2ĵ− 3k̂ ) and r̅ = (î − ĵ+ 2k̂ ) +μ(2î + 4ĵ−5k̂ ) .
Sol. Given lines are r̅ = (4î − ĵ) + λ(î + 2ĵ− 3k̂ ) and r̅ = (î − ĵ+ 2k̂ ) +μ(2î + 4ĵ−5k̂ ) .
Here a̅₁ = 4î − ĵ, b̅₁ = î + 2ĵ−3k̂ and a̅₂= î − ĵ+ 2k̂ , b̅₂ = 2î + 4ĵ− 5k̂

22. Suppose a girl throws a die. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4, 5 or 6, she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, what is the probability that she threw 3, 4, 5 or 6 with the die?
Sol. Let A : getting 1 or 2, B : getting 3, 4, 5 or 6, E : getting exactly one tail.

23. Two numbers are selected at random (without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X.
Sol. Since X denotes the larger of the two numbers obtained from 1, 2, 3, 4, and, 5.
So values of X : 2, 3, 4, 5.
Following is the Probability distribution table : 

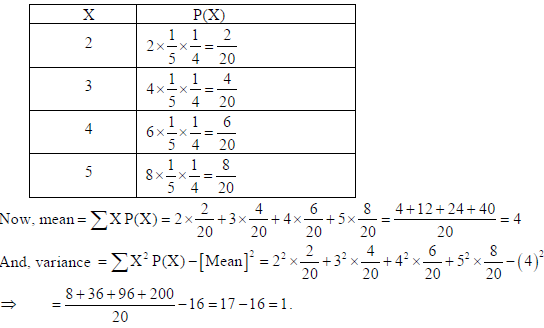
SECTION – D

24. Let A ={x ∈ Z: 0 ≤ x ≤12}. Show that
R = {(a, b) : a,b ∈ A, | a − b | is divisible by 4} is an equivalence relation.
Find the set of all elements related to 1. Also write the equivalence class .
Sol. We have R = {(a, b) : a, b ∈ A, | a − b | is divisible by 4} and
A = {x ∈ Z: 0 ≤ x ≤12} i.e., A = {0,1,2,…,12}.
Reflexivity : For any a ∈ A , we have | a − a | = 0 , which is divisible by 4. That is, (a,a) ∈ R so,
R is reflexive.
Symmetry : Let (a, b) ∈ R ∀ a,b ∈ A . We have | a − b | is divisible by 4.
As | a − b | = | b − a | . So | b − a | is also divisible by 4. That is, (b, a) ∈ R so, R is symmetric.
Transitivity : Let a, b,c ∈ A such that (a, b) ∈ R and (b,c) ∈ R then, | a − b | is divisible by 4 and | b − c | is divisible by 4.
This implies that | a − b | = 4m and | b − c |= 4p where m,p ∈ Z .
As (a − b) + (b − c)= ± 4(m+ p)     ⇒ a − c = ±4(m+ p)      ⇒| a − c |= 4(m+ p) .
That is | a − c | is also divisible by 4 so, R is transitive.
Since the relation R is reflexive, symmetric and transitive so, it is an equivalence relation.
Also the set of all elements related to 1 in relation R is {1, 5, 9}.
Now let (2, x) ∈ R so that |2 – x| is divisible by 4 ∀ x ∈ A .
That is, x = 2,6,10 . Hence [2] = {2, 6, 10}.

OR

Show that the function f :R → R defined by f (x) = x/x²−1 ,∀ x  ∈ R is neither one-one nor onto. Also, if g :R →R is defined as g(x) = 2x −1, find fog (x).  
Sol. 

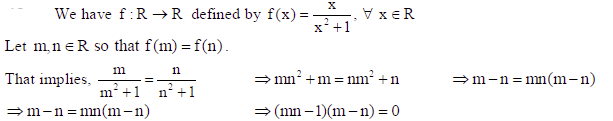
25. 

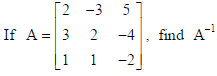
Use it to solve the system of equations 2x − 3y + 5z =11, 3x + 2y − 4z = −5, x + y − 2z = −3.
Sol.

OR

Using elementary row transformations, find the inverse of the matrix

Sol. 

26. Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32 .
Sol. We have y = x…(i), x² + y² = 32…(ii)
Solving (i) & (ii), we get : 2x² = 32 ⇒ x = ±4      ∴ points of intersections : (±4,±4) .

27. Evaluate :

Sol. 

OR

Evaluate

Sol.

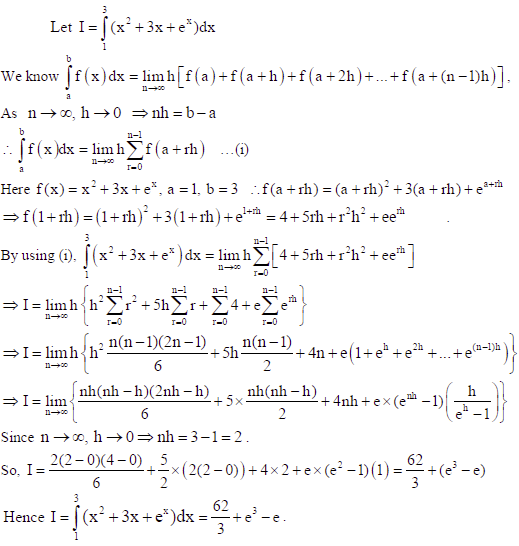
28. Find the distance of the point (–1, –5, –10) from the point of intersection of the line
r̅ = 2î − ĵ+ 2k̂ + λ(3î + 4ĵ+ 2k̂) and the plane r̅.(î − ĵ+ k̂) = 5.
Sol. Since the line r̅ = 2î − ĵ+ 2k̂ + λ(3î + 4ĵ+ 2k̂) and plane r̅.(î − ĵ+ k̂) = 5 intersects each other
so, [2î − ĵ+ 2k̂ + λ(3î + 4ĵ+ 2k̂ )].(î − ĵ+ k̂) = 5
That is, 2+1+ 2 + λ(3− 4 + 2) = 5
⇒ λ = 0
∴ the point of intersection is r̅ = 2î − ĵ+ 2k̂ + 0(3î + 4ĵ+ 2k̂) = 2î − ĵ+ 2k̂ i.e., Q(2,−1,2)
Also let P(–1, –5, –10).

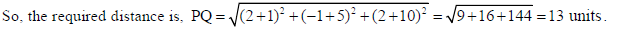
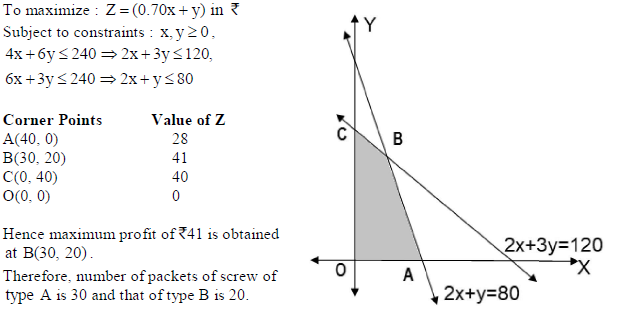
29. A factory manufactures two types of screws A and B, each type requiring the use of two  machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operated machines to manufacture a packet of screws ‘A’ while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a packet of screws ‘B’. Each machine is available for at most 4 hours on any day. The manufacturer can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it
graphically and find the maximum profit.
Sol. Let x and y be the number of packets of screws of type A and type B respectively.