Students can refer to the following MCQ Questions for Class 10 Circles with Answers provided below based on the latest curriculum and examination pattern issued by CBSE and NCERT. Our teachers have provided here a collection of multiple choice questions for Circles Class 10 covering all topics in your textbook so that students can assess themselves on all important topics and thoroughly prepare for their exams
Class 10 Circles MCQs Questions with Answers
We have provided below MCQs questions for Class 10 Circles with answers which will help the students to go through the entire syllabus and practice multiple choice questions provided here with solutions. As Circles MCQs in Class 10 pdf download can be really scoring for students, you should go through all problems provided below and MCQ Questions for Class 10 Maths so that you are able to get more marks in your exams.
Question. In ΔABC, ∠B = 90° .If a circle drawn with AB as diameter intersects the hypotenuse AC at P, which of the following is true?

(a) The tangent drawn to the circle at P bisects the side BC.
(b) The tangent drawn to the circle at A bisects the side AB.
(c) The tangent drawn to the circle at B bisects the side AC.
(d) The tangent drawn to the circle at C bisects the side BC
Ans.
A
Question. PT is a tangent and PAB is a secant of the circle meeting the circle at A and B. If PA = 4 cm and AB = 5 cm. What is the length of PT?
(a) 8 cm
(b) 6 cm
(c) 3 cm
(d) 1 cm
Ans.
B
Question. What is the number of common tangents that can be drawn to two intersecting circles touching at two points?
(a) 2
(b) 4
(c) 3
(d) 1
Ans.
A
Question. AP is a secant and PT is a tangent to a circle. Lf PT=15cm and AB = 8BP, find AP.

(a) 45 cm
(b) 36 cm
(c) 25 cm
(d) 62 cm
Ans.
A
Question. A circle with centre 0 and radius 5 cm is inscribed in an equilateral triangle ABC.

Find the perimeter of ΔABC.
(a) 15√3cm
(b) 25√2 cm
(c) 14√2 cm
(d) 30√3cm
Ans.
D
Question. A tangent ST at P to a circle at P is parallel to a chord QR of the circle.

Which of the following is correct statement?
(a) P is equidistant from the extremities of the chord.
(b) PT is the tangent parallel to the chord PQ.
(c) PT is the tangent parallel to the cord PR.
(d) S is equidistant from the extremities of the chord.
Ans.
A
Question. An isosceles triangle in which AB = AC is inscribed in a circle.

Which of the following is true?
(a) Tangent at A is parallel to BC.
(b) Tangent at A is perpendicular to AB.
(c) Tangent at A is parallel to AC.
(d) Tangent at A is perpendicular to BC.
Ans.
A
Question. In the given figure, 0 is the centre of the circle. PQ is the tangent to the circle and secant PAB passes through the centre O.

If PQ =5 cm and PA = 1 cm, find the radius of the circle.
(a) 8cm
(b) 12cm
(c) 10cm
(d) 6cm
Ans.
B
Question. With the vertices of a ΔABC as centres, three circles are described, each touching the other two externally. If the sides of the triangle are 9 cm, 7 cm and 6 cm, find the radii of the circles.

(a) 4 cm, 7 cm and 3 cm
(b) 7 cm, 5 cm and 2 cm
(c) 5 cm, 4 cm and 3 cm
(d) 4 cm, 5 cm and 2 cm
Ans.
D
Question. If ∠APO = 18°, find ∠AOB.
(a) 24°
(b) 144°
(c) 108°
(d) 1 75°
Ans.
B
Question. In the given figure, ABCD is a quadrilateral in which ∠Q = 90° . A circle C (O, r) touches the sides AB, BC, CD and DA at P, Q, R, S respectively. If BC = 38 cm, CD = 25 cm, and BP = 27 cm, find the value of r.

(a) 14cm
(b) 15cm
(c) 10cm
(d) 16cm
Ans.
A
Question. Tangents AP and AQ are drawn to a circle with centre 0 from an external point A.

Identify the correct statement.
(a) ∠PAQ = 2 ∠OPQ
(b) ∠PAQ = ∠OPQ
(c) ∠PQA = ∠QPA
(d) ∠PQA = 2 ∠OPA
Ans.
B
Question. BD and CD are two tangents drawn to a circle with centre O.

If ∠BDC = 44° ,find ∠BAC.
(a) 68°
(b) 32°
(c) 44°
(d) 96°
Ans.
A
Question. PQ is a chord of a circle .the tangent XR at X on the circle cuts PQ produced at R. If XR = 12 cm , PQ = x cm, QR = (x – 2)cm , find x in cm.
(a) 6
(b) 7
(c) 10
(d) 14
Ans.
C
Question. In the given figure, ABC is an isosceles triangle in which AB = AC.A circle through B touches AC at its mid-point D and intersects AB at P.

Ans.
D
Question. In the above question (no. 3) what is the ratio of AM : BM?
(a) 5 : 6
(b) 3 : 2
(c) 1 : 1
(d) can’t be determined
Answer
C
Question. In the given figure, ABCD is a cyclic quadrilateral and AB is the diameter. ÐADC = 140°, then find m ÐBAC:
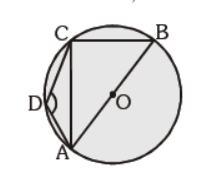
(a) 45°
(b) 40°
(c) 50°
(d) none of the above
Answer
C
Question. DABC and DDBC have a common base and drawn towards one sides. ÐBAC = ÐBDC = 60°. If AC and DB intersect at P, then :
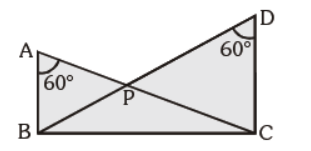
(a) AP × PC = BP × PD
(b) AP × BP = PC × PD
(c) AP × PD = PC × BP
(d) none of these
Answer
A
Question. The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:
(a) rectangle
(b) square
(c) parallelogram
(d) cyclic quadrilateral
Answer
D
Question. In the given figure, ÐAOC = 120°. Find m ÐCBE, where O is the centre:
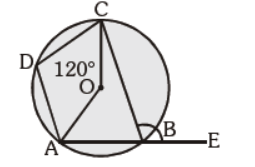
(a) 60°
(b) 100°
(c) 120°
(d) 150°
Answer
C
Question. In the given figure the two chords AC and BC are equal. The radius OC intersect AB at M, then AM : BM is :
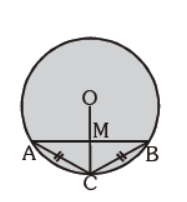
(a) 1 : 1
(b) √2 : 3
(c) 3 : 2
(d) none of the above
Answer
A
Question. In the adjoining figure, O is the centre of circle and diameter AC = 26 cm. If chord AB = 10 cm, then the distance between chord AB and centre O of the circle is :
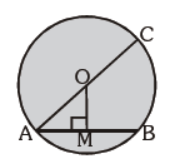
(a) 24 cm
(b) 16 cm
(c) 12 cm
(d) none of the above
Answer
C
Question. In the adjoining circle C (O, r) the degree measure of minor arc AB = 130°. Find the degree measure of major arc :
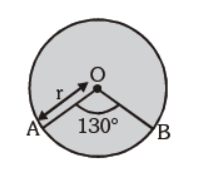
(a) 230°
(b) 260°
(c) 310°
(d) none of the above
Answer
A
Question. In the given figure, ABCD is a cyclic quadrilateral and diagonals bisect each other at P. If ÐDBC = 60° and ÐBAC = 30°, then ÐBCD is :
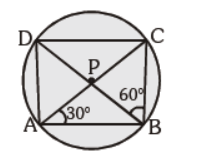
(a) 90°
(b) 60°
(c) 80°
(d) none of the above
Answer
A
Question. If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is
(a) rhombus
(b) square
(c) rectangle
(d) none
Answer
C
Question. In the adjoining figure, O is the centre of the circle and ÐOBD = 50°. Find the m ÐBAD:
(a) 60°
(b) 40°
(c) 80°
(d) 45°
Answer
B
Question. In the given figure, ÐBAC and ÐBDC are the angles of same segments. ÐDBC = 30° and ÐBCD = 110°. Find m ÐBAC is :
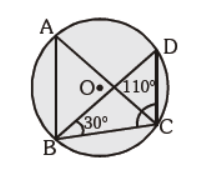
(a) 35°
(b) 40°
(c) 55°
(d) 60°
Answer
B
Question. In the given figure, AB is diameter of the circle. C and D lie on the semicircle. ÐABC = 65° and ÐCAD = 45°. Find m ÐDCA.
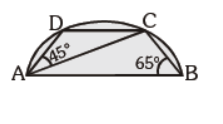
(a) 45°
(b) 25°
(c) 20°
(d) none of these
Answer
C
Question. In the given figure, O is the centre of the circle. Radius of the circle is 17 cm. If OC = 8 cm, then the length of the chord AB is :
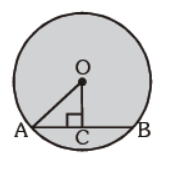
(a) 35 cm
(b) 30 cm
(c) 15 cm
(d) 18 cm
Answer
B
Question. In the given figure, DABC is an equilateral triangle. Find m ÐBEC:
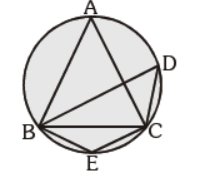
(a) 120°
(b) 60°
(c) 80°
(d) none of the above
Answer
A
Question. In the given figure OM ^ AB, radius of the circle is 5 cm and length of the chord AB = 8 cm. Find the measure of OM :
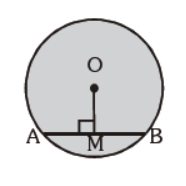
(a) 3 cm
(b) 2.5 cm
(c) 2 cm
(d) 6 cm
Answer
A
Question. In the given figure, AB is the diameter of the circle. Find the value of ÐACD :
(a) 30°
(b) 60°
(c) 45°
(d) 25°
Answer
C
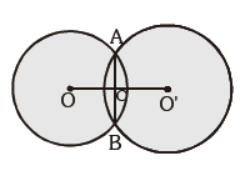
Question. In the given figure, two circles with their respective centres intersect each other at A and B and AB intersects OO’ at M, then m ÐOMA is :
(a) 60°
(b) 80°
(c) 90°
(d) Can’t be determined
Answer
C
Question. In the given figure, chords AB and CD are equal. If ÐOBA = 55° , then m ÐCOD is:
(a) 65°
(b) 55°
(c) 70°
(d) 50° A
Answer
C
Question. In the given figure, O is the centre of the circle. ÐABO = 60°. Find the value of ÐACB :
(a) 40°
(b) 60°
(c) 50°
(d) 30°
Answer
D
Question. In the given figure, O is the centre of the circle and, ÐAOB = 100°. Find m ÐBCD :
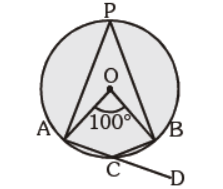
(a) 80°
(b) 60°
(c) 50°
(d) 40°
Answer
C
Question. In the given figure, O is the centre of the circle. ÐAOB = 70°, find m ÐOCD :
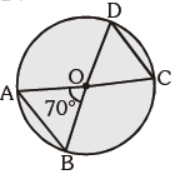
(a) 70°
(b) 55°
(c) 65°
(d) 110°
Answer
B
Question. In the given figure, O is the centre of the circle and ÐACB = 25°. Find ÐAOB :
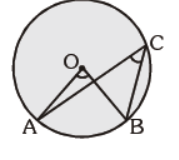
(a) 25°
(b) 50°
(c) 75°
(d) 60°
Answer
B
Question. In the given figure, ABC is an isosceles triangle in which AB = AC and m ÐABC = 50°, m ÐBDC:
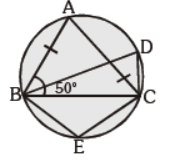
(a) 80°
(b) 60°
(c) 65°
(d) 100°
Answer
A
Question. In the given figure, AB is the diameter, m ÐBAD = 70° and m ÐDBC = 30°. Find m ÐBDC
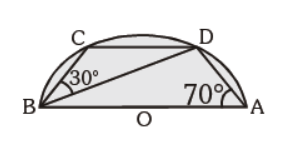
(a) 25°
(b) 30°
(c) 40°
(d) 60°
Answer
C
Question. Find the value of ÐDCE :
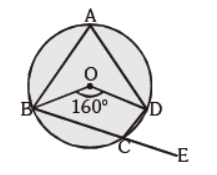
(a) 100°
(b) 80°
(c) 90°
(d) 75°
Answer
B
Question. AB and CD are two parallel of a circle such that AB=10 cm and CD = 24 cm. The chords are on opposite sides of the centre and the distance between them is 17 cm. Find the radius of the circle
(a) 11 cm
(b) 12 cm
(c) 13 cm
(d) 14 cm
Answer
C
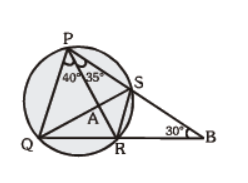
Question. In the given figure, ÐCAB = 40° and ÐAKB = 105°. Find ÐKCD :
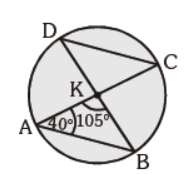
(a) 65°
(b) 35°
(c) 40°
(d) 72°
Answer
B
Question. The line AB is 6 m in length and is tangent to the inner one of the two concentric circle at point C. It is known that the radii of the two circles are integers. The radius of the outer circle.
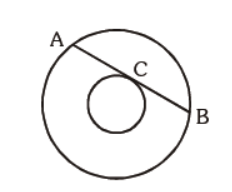
(a)5 m
(b) 4 m
(c) 6 m
(d) 3 m
Answer
A
Question. Find the distance of a perpendicular from the centre of a circle to the chord if the diameter of the circle is 30 cm and its chord is 24 cm.
(a) 6 cm
(b) 7 cm
(c) 9 cm
(d) 10 cm
Answer
C
Question. The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of bigger circle. BD is a tangent to the smaller circel touching it at D. Find the length of AD.
(a) 15 cm
(b) 16 cm
(c) 18 cm
(d) 19 cm
Answer
D
Question. In the given figure, O is the centre of the circle. ÐAOB = 90°. Find m ÐAPB :
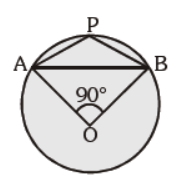
(a) 130°
(b) 150°
(c) 135°
(d) can’t be determined
Answer
C
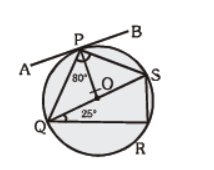
Question. In the given figure, APB is tangent, ÐQPS = 80°, ÐPSQ=65° and ÐSQR = 25°, then
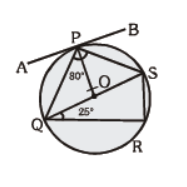
(a) ÐSPB = 35°
(b) ÐAPQ = 65°
(c) ÐQSR = 55°
(d) all of these
Answer
D
Question. In the given figure, O is the centre of the circle. AB is tangent. AB = 12 cm and OB = 13 cm. Find OA:
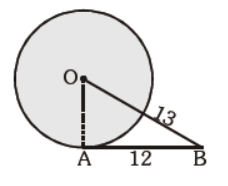
(a) 6.5 cm
(b) 6 cm
(c) 5 cm
(d) none of these
Answer
C
Question. In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R.
PQ = 15 cm, PR = 25 cm, find PN
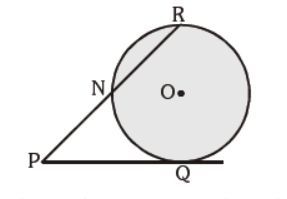
(a) 15 cm
(b) 10 cm
(c) 9 cm
(d) 6 cm
Answer
C
Question. O and O’ are the centres of two circles which touch each other externally at P. AB is a common tangent. Find ÐAPO:
(a) 90°
(b) 120°
(c) 60°
(d) data insufficient
Answer
A
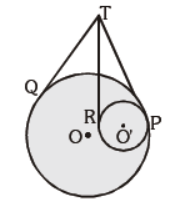
Question. In the given figure, there are two circles with the centres O and O’ touching each other internally at P. Tangents TQ and TP are drawn to the larger circle and tangents TP and TR are drawn to the smaller circle. Find TQ : TR
(a) 8 : 7
(b) 7 : 8
(c) 5 : 4
(d) 1 : 1
Answer
D
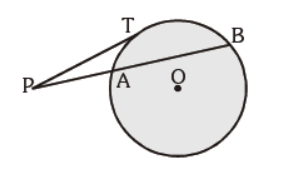
Question. In the given figure, tangent PT = 5 cm, PA = 4 cm, find AB :
(a) 7/ 4 cm
(b) 11/ 4 cm
(c) 9/ 4cm
(d) can’t be determined
Answer
C
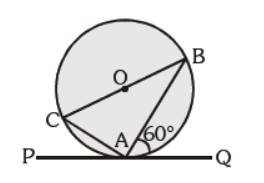
Question. In the given figure, PAQ is the tangent. BC is the diameter of the circle. m ÐBAQ = 60°, find m ÐABC
(a) 25°
(b) 30°
(c) 45°
(d) 60°
Answer
B
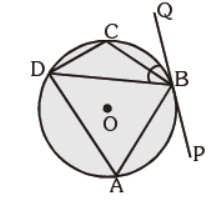
Question. ABCD is a cyclic quadrilateral PQ is a tangent at B. If ÐDBQ = 65° , then ÐBCD is :
(a) 35°
(b) 85°
(c) 115°
(d) 90°
Answer
C
Question. In the given figure, AP = 2 cm, BP = 6 cm and CP = 3 cm. Find DP :
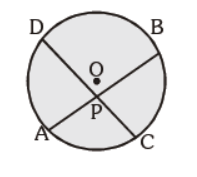
(a) 6 cm
(b) 4 cm
(c) 2 cm
(d) 3 cm
Answer
B
Question. ‘O’ is the centre of the circle, line segment BOD is the angle bisector of ÐAOC, m ÐCOD = 50°. Find m ÐABC:
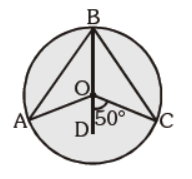
(a) 25°
(b) 50°
(c) 100°
(d) 120°
Answer
B
Question. In the given figure, AP = 3 cm, BA = 5 cm and CP = 2 cm. Find CD :
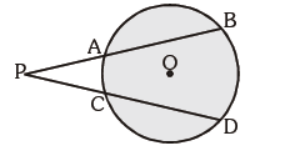
(a) 12 cm
(b) 10 cm
(c) 9 cm
(d) 6 cm
Answer
B
Question. In the given figure, AB is the diameter of the circle. ÐADC = 120°, Find m ÐCAB.
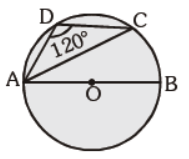
(a) 20°
(b) 30°
(c) 40°
(d) Can’t be determined.
Answer
B
Question. In the given figure, O is the centre of the circle and ÐAOC = 100°. Find the ratio of m ÐADC : m ÐABC
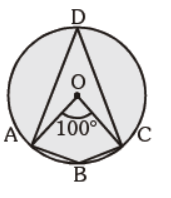
(a) 5 : 6
(b) 1 : 2
(c) 5 : 13
(d) None of the above
Answer
C
Question. Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres
(a) 18 cm
(b) 12 cm
(c) 9 cm
(d) 8 cm
Answer
D
Question. An equilateral triangle has side 2 3 cm. The radius of its circumcircle will be
(a) 2 cm
(b) 3 cm
(c) 3 cm
(d) 4 cm
Answer
A
Question. A circle touches a quadrilateral ABCD. Find the true statement:
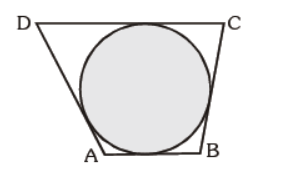
(a) AB + BC = CD + AD
(b) AB + CD = BC + AD
(c) BD = AC
(d) none of the above
Answer
B
Question. In the given fig. PQ is a tangent to the circle at A, ÐBAQ = 50° and ÐBAC = 35°, then ABC=
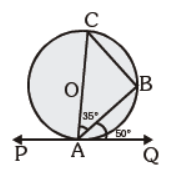
(a) 50°
(b) 35°
(c) 85°
(d) 95°
Answer
D
Question. Three circles touch each other externally. The distance between their centre is 5 cm, 6 cm and 7 cm. Find the radii of the circles :
(a) 2 cm, 3 cm, 4 cm
(b) 3 cm, 4 cm, 1 cm
(c) 1 cm, 2.5 cm, 3.5 cm
(d) 1 cm, 2 cm, 4 cm
Answer
A
Question. In the given figure, O is the centre of circle. ÐAOB = 80° and ÐAOC = 120°. Find m ÐBAC :
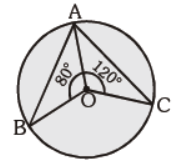
(a) 120°
(b) 80°
(c) 100° C
(d) None of the above
Answer
B
Question. In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
(a) 4.8 cm
(b) 10.8 cm
(c) 9.6 cm
(d) none of these
Answer
C
Question. AB is the chord of a circle with centre O. AB is produced to C, such that BC = OB. CO is joined and produced to meet the circle in D. If ÐACD=y° and ÐAOD = x°, then
(a) 3x°=y°
(b) x°=3y°
(c) x°=y°
(d) x°=4y°
Answer
B
Question. In the adjoining figure, PQRS is a cyclic quadrilateral and the sides PS and QR are produced to meet at B. Then out of the following the true statement is
(a) PR= QS
(b) PB=QB
(c) PR=QB
(d) none of these
Answer
B
Question. In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is :
(a) 23 cm
(b) 30 cm
(c) 15 cm
(d) none of these
Answer
B
Question. In the given figure, AB and CD are two common tangents to the two touching circles. If CD = 6 cm, then AB is equal to:
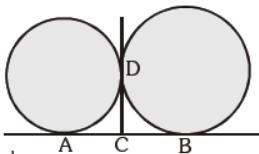
(a) 9 cm
(b) 15 cm
(c) 12 cm
(d) none of the above
Answer
C
Question. In the given figure, ÐCOB = 40°, AB is the diameter of the circle. Find m ÐCAB:
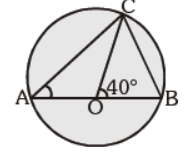
(a) 40°
(b) 20°
(c) 30°
(d) None of these
Answer
B
Question. A circle has two parallel chords of lengths 6 cm and 8 cm. If the chords are 1 cm apart and the centre is on the same side of the chords, then a diameter of the circle is of length:
(a) 5 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm
Answer
D
Question. In a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6 cm. The distance of the chord BC from centre is
(a) 3.6 cm
(b) 1.4 cm
(c) 1 cm
(d) 4 cm
Answer
B
Question. Three equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is :
(a) 6π (2 +√3 )2
(b) 6/π ( 2+√3)2
(c) π/3 (2+√3)2
(d) 3π(2+√3)2
Answer
C
Question. Through any given set of four points P,Q, R, S it is possible to draw :
(a) atmost one circle
(b) exactly one circle
(c) exactly two circles
(d) exactly three circles
Answer
A
Question. O and O’ are the centres of circle of radii 20 cm and 37 cm. AB = 24 cm. What is the distance OO’?
(a) 51 cm
(b) 45 cm
(c) 35 cm
(d) 48 cm
Answer
A
Question. The number of common tangents that can be drawn to two given circles is at the most :
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. In the fig, RTP and STQ are common tangents to the two circels with centres A and B. The radii of the two circles are 3 cm and 5 cm respectively. If ST : TQ = 1 : 3 and RT = 4 cm. Find the length of QT and AB.
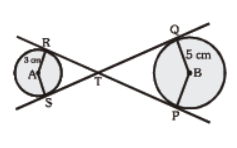
(a) 11 cm, 12 cm
(b) 12 cm, 18 cm
(c) 18 cm, 12 cm
(d) 12 cm, 15 cm
Answer
B
Question. ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is C 5cm 4cm A B 3cm
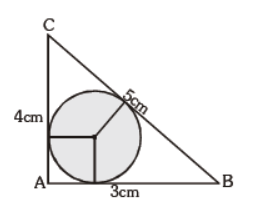
(a) 1 cm
(b) 1.25 cm
(c) 1.5 cm
(d) none of these
Answer
A
Question. In the diagram, PQ and QR are tangents to the circle centre O, at P and R respectively. Find the value of
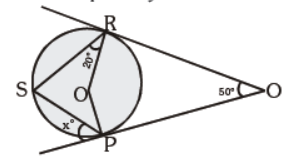
(a) 25
(b) 35
(c) 45
(d) 55
Answer
C
Question. If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
(a) the angle subtended by AB at P and Q are either equal or supplementary.
(b) the sum of the angles subtended by AB at P and Q is always equal two right angles.
(c) the angles subtended at P and Q by AB are always equal.
(d) the sum of the angles subtended at P and Q is equal to four right angles.
Answer
A
Question. The chord ED is parallel to the diameter AC, as shown in the figure. The ___ magnitude of ÐCED is equal to
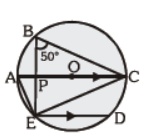
(a) 30°
(b) 40°
(c) 50°
(d) 60°
Answer
B
Question. In the fig., PQ is a tangent to the circle at P. QRS is a straight line. Find the value of x.
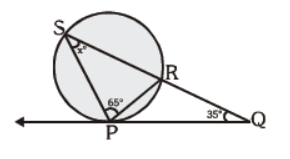
(a) 25°
(b) 30°
(c) 35°
(d) 40°
Answer
D
Question. In the given figure, CD is a direct common tangent to two circles intersecting each other at A and B, then: ÐCAD + ÐCBD = ?
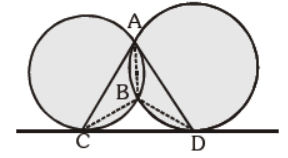
(a) 120°
(b) 90°
(c) 360°
(d) 180°
Answer
D
One Word Question :
Question. Find x and y.
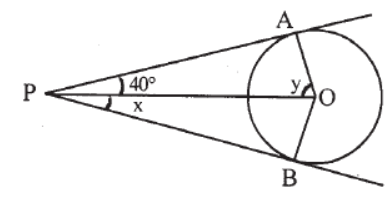
Answer
x = 400 , y = 500
Question. How many lines in this figure are not cutting the circle at all?
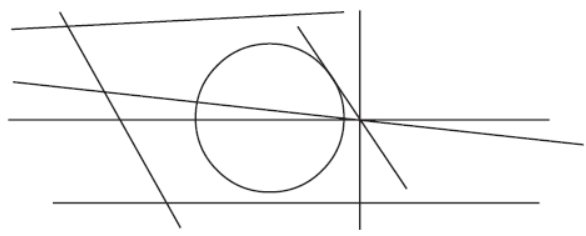
Answer
5
Question. Find ∠BTQ
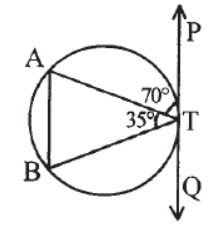
Answer
75°
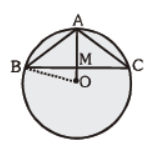
Question. In figure AP = 4cm, OA = 3cm, OB = 2cm. Find BP.
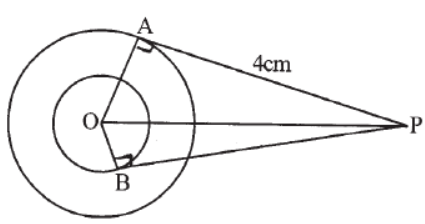
Answer
√21cm
Question. Count number of secants in this figure.
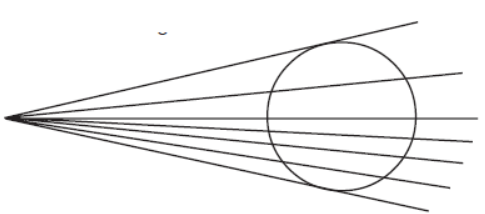
Answer
5
Question. In figure, if PC=CR, then which two sides of a triangle are equal.
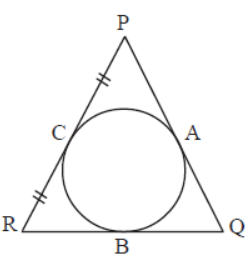
Answer
PQ = QR
Question. In the given figure if AB = 11.5cm and DC = 10.5cm find AD+BC.
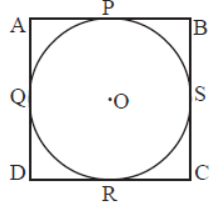
Answer
22cm.
Question. In figure, PA and PB are two tangents drawn from a point P to a circle with centre O touching it at A and B. Then complete the statement : OP is the _________ of AB.
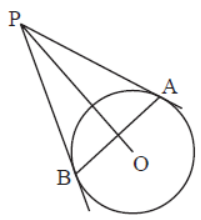
Answer
Perpendicular bisector
Question. Find perimeter of triangle ABC.
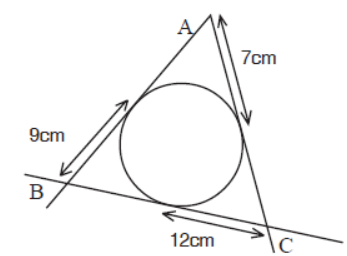
Answer
56cm
Question. In figure, ΔABC touches a circle at a point P. If we extend the sides AB and AC, they touch the circle at Q and R respectively. If the perimeter of a triangle is 12cm, find AQ.
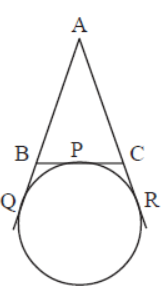
Answer
6cm
Question. If PR=7.5cm, find PS.
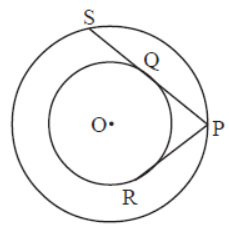
Answer
15cm
Question. Find BC in the given figure.
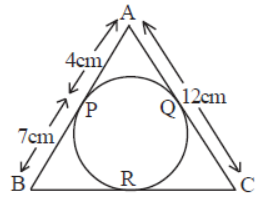
Answer
15cm.
Question. Count the number of tangents in the given figure.
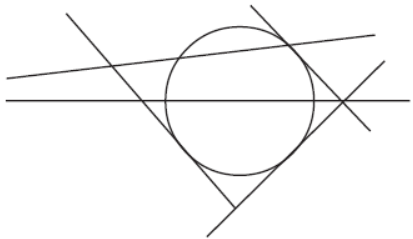
Answer
3
Question. Find OP.
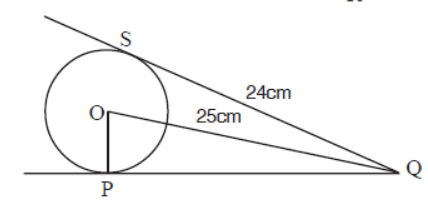
Answer
7cm
Question. How many tangents are there in all in this figure?
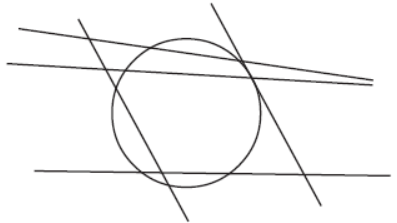
Answer
1
Question. In figure, A point P is 29cm away from the centre of a circle. Find the length of tangent drawn from P to the circle whose radius is 20cm.
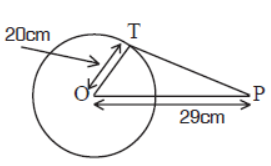
Answer
21cm
Question. Find BP.
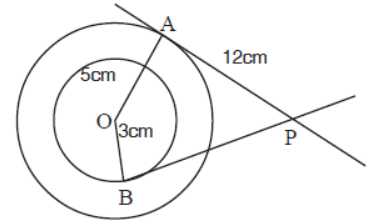
Answer
4 √10cm
Question. Find ∠ACB
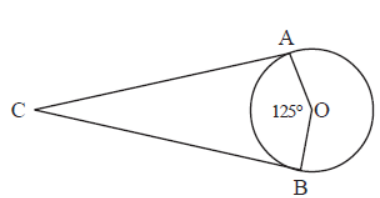
Answer
550
Question. In the figure, the sides of a quad. ABCD touch a circle at P, Q, R and S. Then what is (AB+CD) equal to?
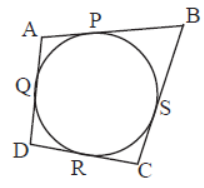
Answer
AD+BC
Question. Find perimeter of ΔPQR
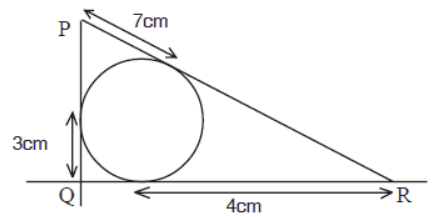
Answer
28cm
