Students can refer to the following Trigonometric Functions MCQ Questions for Class 11 Maths with Answers provided below based on the latest curriculum and examination pattern issued by CBSE and NCERT. Our teachers have provided here a collection of multiple choice questions for Trigonometric Functions Class 11 covering all topics in your textbook so that students can assess themselves on all important topics and thoroughly prepare for their exams
Trigonometric Functions MCQ Questions for Class 11 Maths with Answers
We have provided below Trigonometric Functions MCQ Questions for Class 11 Maths with answers which will help the students to go through the entire syllabus and practice multiple choice questions provided here with solutions. As Trigonometric Functions MCQs in Class 11 Mathematics pdf download can be really scoring for students, you should go through all problems provided below so that you are able to get more marks in your exams.
Question. Difference between the greatest and the least angle is
(a) cos-1 4/5
(b) tan-1 3/4
(c) cos-1 3/5
(d) None of these
Answer
B
Question: The maximum value of
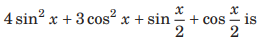
(a) 4 +√2
(b) 3 +√2
(c) 9
(d) 4
Answer
A
Question: cos2θ + 2cos θ is always
(a) greater πthan -3/2
(b) less than or equal to 3/2
(c) greater than or equal to -3/2 and less than or equal to 3
(d) None of the above
Answer
CB
Question: The greatest and least value of sinX cos x are respectively
(a) 1, 1
(b) 1/2,1/2
(c) 1/4,-1/4
(d) 2, -2
Answer
B
Question: The minimum value of 3 cosX+4 sin x + 8 is
(a) 5
(b) 9
(c) 7
(d) 3
Answer
D
Question:
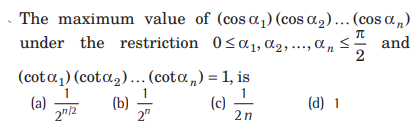
Answer
A
Question. When the elevation of sun changes from 45° to 30°, the shadow of a tower increases by 60 m, then the height of the tower is
(a) 30 √3 m
(b) 30( √2 + 1) m
(c) 30( √3 – 1) m
(d) 30( √3 + 1) m
Answer
D
Question. A flag staff 20 m long standing on a wall 10 m high subtends an angle whose tangent is 0.5 at a point on the ground. If q is the angle subtended by the wall at this point, then
(a) tan θ = 1
(b) tan θ = 3
(c) tan θ = 1/2
(d) None of these
Answer
A
Question. ABis a vertical pole with Bat the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7m. From D the angle of elevation of the point A is 45°. Then, the height of the pole is
(a) 7√3/2(1/√3+1)m
(b) 7√3/2(1/√3-1)m
(c) 7√3/2(√3+1)m
(d) 7√3/2(√3-1)m
Answer
C
Question. A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(= a) subtends an angle of 60° at the foot of the tower and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower is
(a) 2a/√3
(b) 2a√3
(c) a/√3
(d) √3
Answer
C
Question. A ladder rests against a wall making an anglea with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle b with the horizontal. The correct relation is
(a) x = y tan(α+β/2)
(b) y = x tan (α+β/2)
(c) x = y tan(α+β)
(d) y = x tan (α+β)
Answer
A
Question. Consider the following statements
I. If in a ΔABC , sin A/sin C = sin(A-B)sin(B-C) then a2,b2 and c2 are in AP.
II. If exradius r1, r2 and r3 of a DABC are in HP, then the sides a , b and c are in AP.
Which of these is/are correct ?
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) None of these
Answer
C
Question. In a triangle (1-r1/r2)(1-r1/r3)=2 then the triangle is
(a) right angled
(b) equilateral
(c) isosceles
(d) None of these
Answer
A
Question. In a ΔABC, cosec A (sin Bcos C + cos Bsin C) is equal to
(a) c/a
(b) a/c
(c) 1
(d) c/ab
Answer
C
Question. sin A : sin C = sin (A – B) : sin (B – C), then a2 , b2 , c2 , and are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
D
Question. At a distance 2 hm from the foot of a tower of height h m the top of the tower and a pole at the top of the tower subtend equal angles. Height of the pole should be
(a) (5h/3)m
(b) (4h/3)m
(c) (7h/5)m
(d) (3h/2)m
Answer
A
Question. In a ∠ABC, a : b : c = 4 :5 :6. The ratio of the radius of the circumcircle to that of the incircle is
(a) 16/9
(b) 16/7
(c) 11/7
(d) 7/16
Answer
B
Question. If x, y and z are perpendicular drawn from the vertices of triangle having sides a , b and c, then the value of bx/c +cy/a +az/b will be
(a) (a2 + b2 + c2)/2R
(b) (a2 + b2 + c2)/R
(c) (a2 + b2 + c2)/4R
(d) 2(a2 + b2 + c2)/R
Answer
A
Question. A house of height 100msubtends a right angle at the window of an opposite house. If the height of the window be 64 m, then the distance between the two houses is
(a) 48 m
(b) 36 m
(c) 54 m
(d) 72 m
Answer
A
Question. An observer standing on a 300 m high tower observes two boats in the same direction their angles of depression are 60° and 30°, respectively. The distance between boats is
(a) 173.2 m
(b) 346.4 m
(c) 25 m
(d) 72 m
Answer
B
Question. An observer on the top of tree, finds the angle of depression of a car moving towards the tree to be 30°.After 3 min this angle becomes 60°. After how much more time, the car will reach the tree ?
(a) 4 min
(b) 4.5 min
(c) 1.5 min
(d) 2 min
Answer
C
Question. The horizontal distance between two towers is 60 m and the angle of depression of the top of the first tower as seen from the top of the second is 30°. If the height of the second tower be 150 m, then the height of the first tower is
(a) (150 – 60√3) m
(b) 90 m
(c) (150 – 20√3) m
(d) None of these
Answer
D
Question. An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60° and after 10 s the elevation is observed to be 30°. The uniform speed of the aeroplane (in km/h) is
(a) 240
(b) 240√3
(c) 60√3
(d) None of the above
Answer
B
Question. Points D, E are taken on the side BC of a ΔABC such that BD = DE = EC. If ∠BAD =x , ∠DAE =y , ∠EAC = z, then the value of sin(x+y) sin (y+z) /sinx sinz is equal to
(a) 1
(b) 2
(c) 4
(d) None of these
Answer
C
Question. In a ΔABC, if a = 2 x, b = 2y and ÐC = 120°, then the area of the triangle is
(a) xy sq unit
(b) xy √3 sq unit
(c) 3xy sq unit
(d) 2 xy sq unit
Answer
B
Question. In ΔABC, if tan A/2 tan C/2 = 1/2 then a , band c are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
D
Question. A flag staff is upon the top of a building. If at a distance of 40 m from the base of building the angles of elevation of the topes of the flag staff and building are 60° and 30° respectively, then the height of the flag staff is
(a) 46.19 m
(b) 50 m
(c) 25 m
(d) None of these
Answer
A
Question. At a point on the ground the angle of elevation of a tower is such that its cotangent is 3/5 . On walking 32 m towards the tower the cotangent of the angle of elevation is 2/5. The height of the tower is
(a) 160 m
(b) 120 m
(c) 64 m
(d) None of these
Answer
A
Question. From the bottom of a pole of height h the angle of elevation of the top of a tower is a and the pole subtends an angle b at the top of the tower. The height of the tower is
(a) h tan(α-β) /tan(α-β) -tanα
(b) h cot(α-β) /cot(α-β) -cotα
(c) cot(α-β) / cot(α-β) -cotα
(d) None of these
Answer
B
Question. Each side of a square subtends an angle of 60° at the top of a towerh metres high standing in the centre of the square. If ais the length of each side of the square, then
(a) 2a2 = h2
(b) 2h2 = h2
(c) 3a2 = 2h2
(d) 2h2 = 3a2
Answer
B
Question. The top of a hill observed from the top and bottom of a building h is at angles of elevation p and q, respectively. The height of hill is
(a) h cot q/ cotq – cotp
(b) h cot p/ cotp – cotq
(c) h tan p /tanp – tanq
(d) None of these
Answer
B
Question. ABC is a triangular park with AB = AC = 100 m. A clock tower is situated at the mid-point of BC. The angles of elevation of the top of the tower at A and B are cot-1 3.2 and cosec-1 2.6, respectively. The height of the tower is
(a) 50 m
(b) 25 m
(c) 40 m
(d) None of these
Answer
B
Question. The angle of elevation of the top of a tower from a point A due South of the tower is a and from a point Bdue East of the tower isb. If AB= d, then the height of the tower is
(a) d/√tan2α – tan2β
(b) d/√tan2α + tan2β
(c) d/√cot2α + cot2β
(d) d/√cot2α – cot2β
Answer
C
Question. ABCD is a square plot. The angle of elevation of the top of a pole standing at Dfrom A orC is 30° and that from B is q, then tan q is equal to
(a) 6
(b) 1/√6
(c) √3/2
(d) √(2 /3)
Answer
B
Question. A vertical tower stands on a declivity which is inclined at 15° to the horizon. From the foot of the tower a man ascends the declivity for 80 ft and then, finds that the tower subtends an angle of 30°. The height of tower is
(a) 20(√6 – √2) ft
(b) 40(√6 – √2) ft
(c) 40(√6 + √2) ft
(d) None of these
Answer
B
Question. If A and B are two points on one bank of a straight river and C, D are two other points on the other bank of river. If direction from A to B is same as that from C to D and AB = a, ∠CAD = a, ∠DAB = b, ∠CBA = g, then CD is equal to
(a) a sinβ sinγ /sinαsin(α + β + γ)
(b) a sinα sinγ /sinβsin(α + β + γ)
(c) a sinα sinβ /sinβsin(α + β + γ)
(d) None of these
Answer
B
Question. The angle of elevation of the top of a hill from a point is a. After walking b m towards the top up a slope inclined at an ∠β to the horizon, the angle of elevation of the top becomes γ. Then, the height of the hill is
(a) b sinα sin (γ – β)/sin (γ – α)
(b) b sinα sin (γ – α)/sin (γ – β)
(c) b sin(γ – β) /sin (γ – α)
(d) sin(γ – β)/b sinα sin(γ – α)
Answer
A
Question. The angle of elevation of a cloud at a point 2500 m high above a lake is 15° and the angle of depression of its image in the lake is 45°, the height of the cloud above the surface of
the lake is
(a) 2500√3 m
(b) 2500 m
(c) 500√3 m
(d) 500 m
Answer
B
Question. In an isosceles D ABC, AB = AC. If vertical ΔA is 20°, then a3 + b3 is equal to
(a) 3a2b
(b) 3b2c
(c) 3c2a
(d) abc
Answer
C
Question. If A, B, C, D are the angles of a quadrilateral, then ∑tanA/∑cotA is equal to
(a) π tan A
(b) π cot A
(c) ∑ tan2 A
(d) ∑ cot2 A
Answer
A
Question. In a ΔABC, (a + b + c)(b + c – a) = kbc, if
(a) k < 0
(b) k > 6
(c) 0 < k < 4
(d) k > 4
Answer
C
Question. In an acute angled ΔABC, r + r1 = r1+ r2 + r3 and ∠B >π/3, then
(a) b + 2c < 2a < 2b + 2c
(b) b + 4c < 4a < 2b + 4c
(c) b + 4c < 4a < 4b + 4c
(d) b + 3c < 3a < 3b + 3c
Answer
D
Question. For a ΔABC, R = 5/2 and r = 1. Let I be the incentre of the triangle and D, E and F be the feet of the perpendiculars from I to BC, CA and AB,respectively. The value of ID X IE X IF/IA X IB X IC is equal to
(a) 5/2
(b) 5/4
(c) 1/10
(d) 1/5
Answer
C
Question. The area of the circle and the area of a regular polygon of n sides and of perimeter equal to that of the circle are in the ratio of
(a) tan(π/n) : π/n
(b) cos (π/n) : π/n
(c) sin (π/n) : π/n
(d) cot (π/n) : π/n
Answer
A
Question. The radii r r r 1 2 3 , , of the described circles of the DABC are in HP. If the area of the triangle is 24 2 cm and its perimeter is 24 cm, then the length of its largest side
is
(a) 10
(b) 9
(c) 8
(d) 7
Answer
A
Question. From the top of a cliff of height a , the angle of depression of the foot of a certain tower is found to be double the angle of elevation of the top of the tower of height h. If q be the angle of elevation, then its value is (a) rcosec sinβ (b) rcosec α sin
(a) cos-1√(2h/a)
(b) sin-1 √(2h/a)
(c) sin-1 √(a/2-h)
(d) tan-1√(3 -2h/a)
Answer
D
Question. From a point a metres above a lake the angle of elevation of a cloud is α and the angle of depression of its reflection is β. The height of the cloud is
(a) asin(α+β) /sin(α-β) m
(b) asin(α+β)/sin(β-α) m
(c) asin(β-α)/sin(α+β) m
(d) None of these
Answer
B
Question. If PQbe a vertical tower subtending anglesa, b and g at the points A, B and C respectively on the line in the horizontal plane through the foot Dof tower and on the same side of it, then BC cota – CA cotb + ABcot g is equal to
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
A
Question. A flag staff stands in the centre of a rectangular field whose diagonal is 1200 m and subtends angles 15° and 45° at the mid-points of the sides of the field. The height of the flag staff is
(a) 200 m
(b) 300 √2 + √3 m
(c) 300 √2 – √3 m
(d) 400 m
Answer
C
Question. At each end of a horizontal line of length 2a, the angular elevation of the peak of a vertical tower is q and that at its middle point it is f. The height of the peak is
(a) a sin θ sin Φ
(b) a sin θ sin Φ /√sin(θ+Φ)sin(θ-Φ)
(c) a cosθ cosΦ /√cos(θ+Φ)cos(θ-Φ)
(d) None of the above
Answer
B
Question. In a cubical hall ABCDPQRS with each side 10 m,G is the centre of the wall BCRQand T is the mid-point of the side AB. The angle of elevation of G at the point T is
(a) sin-1 (1/√3)
(b) cos-1 (1/√3)
(c) cot-1 (1/√3)
(d) None of these
Answer
A
Question. Two vertical poles 20 m and 80 m stands apart on a horizontal plane. The height of the point of intersection of the lines joining the top of each pole to the foot of the other is
(a) 15 m
(b) 16 m
(c) 18 m
(d) 50 m
Answer
A
Question. Let ABC be an isosceles triangle with base BC. If r is the radius of the circle inscribed in the ΔABC and r1 be the radius of the circle escribed opposite to the angle A, then the product r1r can be equal to
(a) R2 sin2A
(b) R2 sin2B
(c) 1/2a2
(d) a2/4
where R is the radius of the circumcircle of the ΔABC.
Answer
C
Question. Circumradius R is equal to
(a) 2.5
(b) 3.5
(c) 1.5
(d) 4.2
Answer
A
Question. For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is
(a) there is a regular polygon with r/R = 1/2
(b) there is a regular polygon with r/R = 1/√2
(c) there is a regular polygon with r/R = 2/3
(d) there is a regular polygon with r/R =√3/2
Answer
D

We hope you liked Trigonometric Functions MCQ Questions for Class 11 Maths provided above. If you have any questions, please post them in the comments box below. Our teachers will provide a response.