Please refer to Class 12 Mathematics Sample Paper Term 1 With Solutions Set D provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Term 1 Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
Term 1 Sample Paper for Class 12 Mathematics With Solutions Set D
Section A
In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.
1. Let Z = x + y be the objective function and maximumZ = 30. The maximum value occurs at point
(a) (50/3 , 40/3)
(b) (0, 0)
(c) (25, 0)
(d) (0, 20)
Answer
A
2. The slope of the tangent of the curve x = 3t2 + 13t + 8 and y = 12t2 + 2t -15 at t = 5, is
(a) 7/6
(b) 122/43
(c) 1
(d) 5/6
Answer
B
3. The slope of the normal to the curve ay2 = x3 at the point (am2 , am3) is
(a) 3m
(b) 1/3m
(c) -3m/2
(d) -2/3m
Answer
D
4. The least value of a such that the function f given by f(x) = x2 + ax + 1 is strictly increasing on (1, 2) is
(a) -1
(b) -2
(c) 0
(d) 1
Answer
A
5. If f(x) =
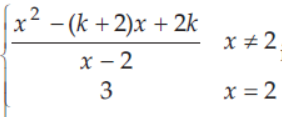
is continuous at x = 2, then k is equal to
(a) 1
(b) -1
(c) 0
(d) 4
Answer
B
6. If A is a skew-symmetric matrix of order 3, then the value of|A|is
(a) 3
(b) 0
(c) 9
(d) 27
Answer
B
7. If
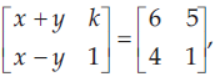
then the value of x and y are respectively
(a) 5 and 1
(b) 1 and 5
(c) 3 and 5
(d) 5 and 3
Answer
A
8. If A = [aij] 3x2 is a matrix given by A =
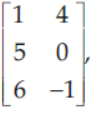
then a22 a31 + is equal to
(a) 1
(b) 6
(c) 0
(d) -1
Answer
B
9. If A =
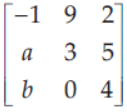
is upper triangular matrix, then a + b is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
10. The value of sin-1(sin 3π/4) is
(a) 3π/4
(b) π/4
(c) 5π/4
(d) None of these
Answer
B
11. If tan-1(1) = sin-1 x , then the value of x is
(a) √3/2
(b) 0
(c) 1/2
(d) 1/√2
Answer
D
12. The relation S is defined on the set of integers Z as xSy, if integer x divides integer y. Then,
(a) S is an equivalence relation
(b) S is only reflexive and symmetric
(c) S is only reflexive and transitive
(d) S is only symmetric and transitive
Answer
C
13. Let P = {1, 2, 3} and a relation on set P is given by the set R = {(1, 2), (1, 3), (2, 1), (1, 1), (2, 2), (3, 3), (2, 3)}. Then, R is
(a) reflexive, transitive but not symmetric
(b) symmetric, transitive but not reflexive
(c) symmetric, reflexive but not transitive
(d) None of these
Answer
A
14. Let A = {1, 2, 3}. We defined R1 = { (1, 2), (3, 2), (1, 3)} and R2 = {(1, 3), (3, 6), (2, 1), (1, 2)}.
Then, choose the correct option.
(a) R1 is relation and R2 is not
(b) R1 and R2 is relation
(c) R1 and R2 are both non-relation
(d) None of these
Answer
A
15. LetW denotes the set of all non-negative integers and Z denotes the set of all integers.
The function f :Z → W given by f (x) =|x|is
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
Answer
B
16. Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}.
Choose the correct answer.
(a) (2, 4) ∈ R
(b) (3, 8) ∈ R
(c) (6, 8) ∈ R
(d) (8, 7) ∈ R
Answer
C
17. The area of the triangle with vertices (- 1, 2), (4, 0) and (3, 9) is k sq units, then value of k is
(a) 43
(b) 43/2
(c) 20
(d) 43/3
Answer
B
18. If Δ =

then the value of a11M11 – a12M12 a13M13 + is
(a) 10
(b) 8
(c) 14
(d) 4
Answer
B
19. If y = √x+1 + √x-1 , then √x2-1 dy/dx is equal to
(a) y
(b) y/2
(c) y/3
(d) – y
Answer
B
20. If y = log(cos x2) , then dy/dx is equal to
(a) – 2x cot x2
(b) – 2x tan x2
(c) 2x tan x2
(d) None of these
Answer
B
Section B
In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.
21. If f(x) =
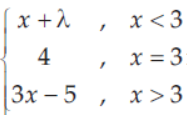
is continuous at x = 3, then the value of λ is
(a) 4
(b) 3
(c) 2
(d) 1
Answer
D
22. If the function f(x) =
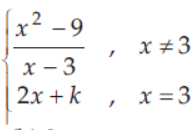
is continuous at x = 3, then the value of k is
(a) 3
(b) 0
(c) – 6
(d) 1
Answer
B
23. If
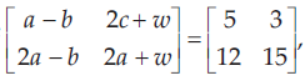
then the value of a, b, c and w are respectively
(a) 1, 1, 2 and 7
(b) 7, 1, 2 and 1
(c) 1, 2, 7and 7
(d) 7, 2, 1 and 1
Answer
D
24. The relation R in the set Z of integers given by R = {(a, b) : a – b is divisible by 5} is
(a) reflexive
(b) reflexive but not symmetric
(c) symmetric and transitive
(d) an equivalence relation
Answer
D
25. If A =
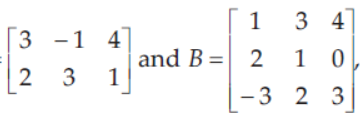
then AB is equal to
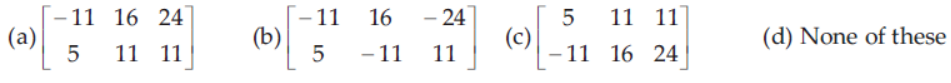
Answer
A
26. If A =
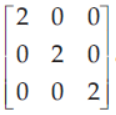
and A4 = kA , then k is equal to
(a) 10
(b) 16
(c) 32
(d) 8
Answer
D
27. If A =
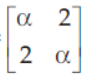
and|A3| = 125, then a is equal to
(a) ± 3
(b) ± 5
(c) 0
(d) ± 2
Answer
A
28. If A =
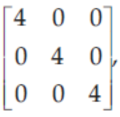
then |adj A|is equal to
(a) 43
(b) 46
(c) 42
(d) 45
Answer
B
29. If Δ =
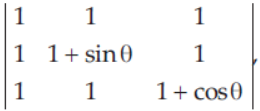
then the maximum value of Δ is
(a) 1
(b) 1/2
(c) 1/3
(d) 0
Answer
B
30. In the interval π/2 < x < π , then value of x for which the matrix
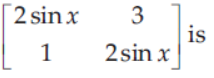
singular is
(a) π/2
(b) π/6
(c) π/3
(d) 2π/3
Answer
D
31. If the function f(x) =
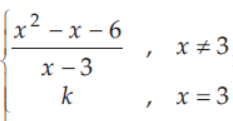
is continuous at x = 3, then the value of k is
(a) 5
(b) 4
(c) 3
(d) 2
Answer
A
32. If the function f(x) =
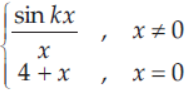
is continuous at x = 0. Then, the value of k is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
D
33. If y = x +√x2-1 , then (y – x) dy/dx is equal to
(a) – y
(b) y
(c) y2
(d) 1/y
Answer
B
34. If f (x) = x tan- 1 x, then f ‘ (1) is equal to
(a) 1 + π/4
(b) 1/2 – π/4
(c) 1/2 + π/4
(d) 2
Answer
C
35. If x2/a2 + y2/b2 = 10 , then dy/dx at (a2 , b2) is equal to
(a) 1
(b) – 1
(c) 0
(d) 2
Answer
B
36. The function f(x) = x2e-x is increasing in the interval
(a) (- ∞, ∞)
(b) (- 2, 0)
(c) (0, 2)
(d) (2, ∞)
Answer
C
37. In the interval (- 3, 3), the function f(x) = x/3 + 3/x , x ≠ 0 is
(a) decreasing
(b) increasing
(c) neither increasing nor decreasing
(d) None of these
Answer
A
38. The slope of the normal to the curve x = a cos3 θ and y = a sin3 θ at θ = π/4 is
(a) 1
(b) – 1
(c) 0
(d) 2
Answer
A
39. The equation of normal to the curve y = 2x2 + 3 sin x at (0, 0) is
(a) x + 3y = 0
(b) x – 3y = 0
(c) y – 3x = 0
(d) y + 3x = 0
Answer
A
40. If A2 – 5A + 71 = O , then A-1 is equal to
(a) 1/7 (A-5I)
(b) 1/7(5I-A)
(c) -1/7(5I-A)
(d) None of these
Answer
B
Section C
In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.
41. The function f (x) = x3 – 3x2 + 6x + 3 has
(a) maximum value at x = 1
(b) minimum value at x = 0
(c) neither a maximum nor a minimum value
(d) None of the above
Answer
C
42. If A =
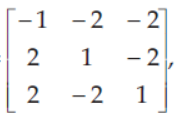
then adj A is equal to

Answer
A
43. Let f (x) = (1 + b2 )x2 + 2bx + 1 and m(b) be the minimum value of f (x). As b varies, the range of m(b) is
(a) [0, 2]
(b) [0,1/2]
(c) [1/2 , 1]
(d) (0, 1]
Answer
D
44. In the interval [1, ∞), the function f (x) = (x + 1)3 (x – 3)3 is
(a) increasing
(b) decreasing
(c) neither increasing nor decreasing
(d) None of these
Answer
A
45. If f (x) = xex(x-1) , then f(x) is
(a) increasing on [-1/2 , 1]
(b) decreasing on R
(c) increasing on R
(d) decreasing on [-1/2 , 1]
Answer
A
CASE STUDY
The feasible solution for a LPP is shown below.
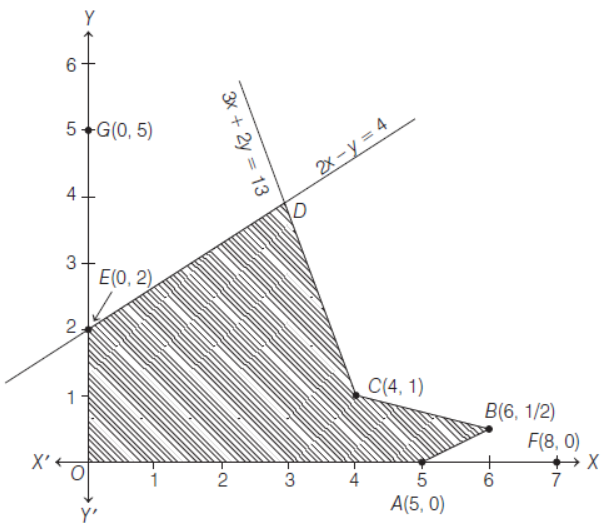
and the objective function is Z = 15x – 4y.
Based on the above information, answer the following questions.
46. The coordinate of point D is
(a) (1, 2)
(b) (2, 2)
(c) (3, 2)
(d) (4, 2)
Answer
C
47. The value of (n – 1)2 , where nis number of corner points, is
(a) 36
(b) 25
(c) 16
(d) 9
Answer
B
48. The maximum of Z is
(a) 88
(b) 75
(c) 56
(d) 89
Answer
A
49. The minimum of Z is
(a) 0
(b) 37
(c) 1
(d) -8
Answer
D
50. Z (6,1/2) + Z (0,2) is equal to
(a) 88
(b) 80
(c) 82
(d) 86
Answer
B