Students can read the important questions given below for Application of Derivatives Class 12 Mathematics. All Application of Derivatives Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Application of Derivatives Class 12
Very Short Answer Type Questions
Question. Find the slope of the tangent to the curve y = 3x2 – 6x at the point on it whose x-coordinate is 2.
Answer. y = 3x2 – 6x

Question. The total cost C(x) associated with provision of free mid-day meals to x students of a school in primary classes is given by C(x) = 0.005x3 – 0.02x2 + 30x + 50 If the marginal cost is given by rate of change dc/dx of total cost, write the marginal cost of food for 300 students.
Answer. C(x) = 0.005x3 – 0.02x2 + 30x + 50
Differentiating w.r.t. x, we have
= C'(x) = 0.015x2 – 0.04x + 30
When x = 300, C'(300) = 0.015(90,000) – 0.04(300) + 30 = ₹(1,350 – 12 + 30) = ₹ 1368 ₹ Marginal cost of food for 300 students is ₹ 1,368
Question. Write the equation of tangent drawn to the curve y = sin x at the point (0, 0).
Answer. y = sin x
Differentiating both sides w.r.t. x

∴ Slope of tangent, m = 1
Equation of the tangent at point (0, 0) and slope 1 is
(y – 0) = 1(x – 0) ⇒ y – x = 0
Short Answer Type Questions-I
Question. Show that the function f (x) = 4x3 – 18x2 + 27x – 7 is always increasing on R.
Answer. f(x) = 4x3 – 18x2 + 27x – 7
Differentiating both sides w.r.t. x, we have
f(x) = 12x2 – 36x + 27
= 3[4x2 – 12x + 9]
= 3[(2x)2 – 2(2x)(3) + (3)2]
= 3(2x – 3)2 x ∈ R
When x ∈ R, 3(2x – 3)2 > 0
f'(x) > 0 for all
Hence, f(x) is increasing on R.
Question. For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
Answer.

Answer.

Thus, slope of curve is decreasing at the rate of 72 units/sec when x is increasing at the rate of 2 units/ sec.
Question. Show that the function f (x) = x3 – 3×2 + 6x – 100 is increasing on R.
Answer. f (x) = x3 – 3×2 + 6x – 100
Differentiating both sides w.r.t. x, we have
f(x) = 3×2 – 6x + 6
= 3(x2 – 2x + 2)
= 3[x2 – 2x + 1 + 1]
= 3[(x – 1)2 + 1]
When x ∈ R, 3[(x – 1)2 + 1] > 0
f(x) > 0 for all x ∈ R.
Hence, f (x) is increasing on R.
Question. A particle moves along the curve 6y = x3 + 2. Find the points on the curve at which
y-coordinate is changing 2 times as fast as
x-cordinate.
Answer. y-coordinate is changing 2 times as fast as x-coordinate

Question. The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r = 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.
Answer.

Short Answer Type Questions-II
Question. Find the intervals in which the function f given by f (x) = sin x + cos x, 0 < x < 2π, is strictly increasing or strictly decreasing.
Answer. f (x) = sin x + cos x, 0 < x < 2π
∴ f(x) = cos x – sin x
f(x) = 0, ∴ cos x – sin x = 0
⇒ – sin x = – cos x ⇒ tan x = 1


Question. Find the intervals in which the function f (x) = (x – 1) (x – 2)2 is (a) increasing,
(b) decreasing.
Answer. f (x) = (x – 1) (x – 2)2
Differentiating both sides, w.r.t. x, we get
f(x)= (x – 1).2(x – 2) + (x – 2)2.1
= (x – 2) [2x – 2 + x – 2]
= (x – 2) (3x – 4)
For stationary point, f ’(x) = 0
∴ (3x – 4) or (x – 2) = 0
⇒ 3x = 4 or x = 2
⇒ x = 4/3
or x = 2

Question. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of (a) the perimeter, (b) the area of the rectangle.
Answer.

Long Answer Type Questions
Question. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs ₹ 70 per sq. metre for the base and ₹ 45 per sq. metre for sides, what is the cost of least expensive tank?
Answer. Let x m be the length and y m be the breadth of open tank
Volume of tank = 8 m3



Question. A manufacturer can sell x items at a price of

Answer.


Question. Find a point on the curve y2 = 2x which is at a minimum distance from the point (1, 4).
Answer.



Question. Find the equations of the tangent and the normal to the curve
x = 1 – cos θ ; π = θ – sin θ at θ = π/4.
Answer. x = 1 – cos θ, y = θ – sin θ
Differentiating both sides w.r.t. θ, we get



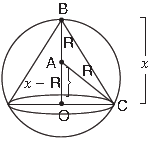
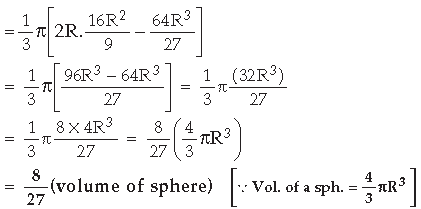
Question. Show that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.
Answer. Let x be the height of cone which is inscribed in a sphere.


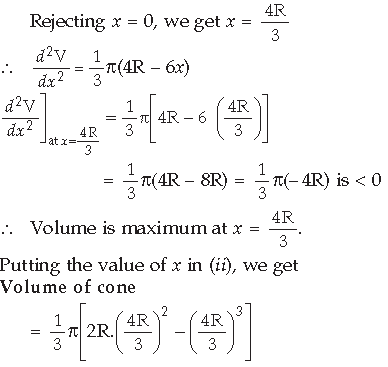
Question. An open tank with a square base and vertical sides is to be constructed From a metal sheet so as to hold a given quantity of water. Show that the total surface area is least when depth of the tank is half of its width.
Answer. Let length of an open tank, l = x
Width/breadth of an open tank, b = x
and depth/height of an open tank, h = y
Vol. of open tank (cuboid), V = k (a constant)


81. A wire of length 28 m is to be cut into two pieces. One of the two pieces is to be made into a square and the other into a circle. What should be the lengths of two pieces so that the combined area of circle and square is minimum?
Answer.




