Question. Let A = {1, 2, 3, 4}. Let R be the equivalence relation on A × A defined by (a, b) R (c, d) if a + d = b + c. Then the equivalence class [(1, 3)] is
(a) {(1, 3)}
(b) {(2, 4)}
(c) {(1, 8), (2, 4), (1, 4)}
(d) {(1, 3) (2, 4)}
Answer
D
Question. Which of the following functions form Z into Z bijections?
(a) f (x) = x3
(b) f (x) = x + 2
(c) f (x) = 2x + 1
(d) f (x) = x2 + 1
Answer
B
Question. The point on the curve y2 = x, where the tangent makes an angle of x / 4 with x-axis is
(a) (1/ 2, 1/ 4 )
(b) (1/ 4 ,1/ 2)
(c) (4, 2)
(d) (1, 1)
Answer
B
Question. The function f (x) = tan x – x
(a) always increases
(b) never increases
(c) always decreases
(d) sometimes increases and sometimes decreases
Answer
A
Question. The derivative of cos x w.r.t. sin x is
(a) cot x
(b) tan x
(c) – cot x
(d) – tan x
Answer
D
Question. If y = √sin x + y , then dy/ dx is equal to
(a) cos x /2y − 1
(b) cos x/ 1 − 2y
(c) sin x/ 1 − 2y
(d) sin x /2y − 1
Answer
A
Question. The equation of tangent drawn to the curve y = sin x, at the point (0, 0) is
(a) y + x = 1
(b) y – x = 1
(c) y + x = 0
(d) y – x = 0
Answer
D
Question. If tan–1 x + tan–1 y = 4π/5 , then cot–1 x + cot–1 y equals
(a) π / 5
(b) 2π/5
(c) 3π/5
(d) π
Answer
A
Question. If f : R → R be defined by f(x) = 2 x , x ∀ R, then f is
(a) one-one
(b) onto
(c) bijective
(d) f is not defined
Answer
D
Question. If A = [cosθ sinθ / – sinθ cosθ] n ∈ N , then value of Det (An) is
(a) –1
(b) 0
(c) n
(d) 1
Answer
D
Question. Find the point on the curve y = x2 – 2x + 3, when the tangent is parallel to x-axis.
(a) (1, 2)
(b) (2, 1)
(c) (– 1, 2)
(d) (1, – 2)
Answer
A
Question. The value of |3I3| is …… when I3 is the identity matrix of order 3
(a) 3
(b) 9
(c) 27
(d) 81
Answer
C
Question. The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(a) (1, 2)
(b) (2, 1)
(c) (1, – 2)
(d) (– 1, 2)
Answer
A
Question. Differentiate cos2(x3) w.r.t. x3 is equal to
(a) – cos(2x3)
(b) –sin(2x3)
(c) sin(2x3)
(d) cos (2x3)
Answer
B
Question. The function f (x) = [x], where [x] denotes the greatest integer function, is continuous at
(a) – 5
(b) 6
(c) – 2.4
(d) 376
Answer
C
Case Study :
Read the given para and answer the following MCQs by choosing the most appropriate option
q A trust fund has `35,000 that must be invested in two different types of bonds, say X and Y. The first bond pays 10% interest p.a. which will be given to an old age home and second one pays 8% interest p.a. which will be given to WWA (Women Welfare Assocation). Let A be a 1 × 2 matrix and B be a 2 × 1 matrix, representing
the investment and interest rate on each bond respectively.
Question. If `15,000 is invested in Bond X, then
(a) A = Investment X/ Y [15000 /20 000] ; B = [X /0.1 , Y / 0 08] Interest rate
(b) A = Investment X/ Y [X /15000, Y/20 000] ; B = X/Y[0.1/0.08]
(c) A = Investment [X/ 20000 ,Y/ 15 000] ; B = X/Y[0.08/0.1] Interest Rate
(d) None of these
Answer
B
Read the given para and answer the following MCQs by choosing the most appropriate option
q Shobhit′s father wants to construct a rectangular garden using a brick will on one side of the garden and wire fencing for the other three sides as shown in figure. He has 200 ft. of wire fencing.
Question. Area of the garden as a function of x, say A(x), can be represented as
(a) 200 + 2x2
(b) x – 2x2
(c) 200x – 2x2
(d) 200 – x2
Answer
C
Question. Maximum value of A(x) occurs at x equals
(a) 50 ft.
(b) 30 ft.
(c) 26 ft.
(d) 31 ft.
Answer
A
Read the given para and answer the following MCQs by choosing the most appropriate option
q The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. ‘A’ is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby, Ram Robert and Rahim suggested to the film to place the hoarding board at three different locations namely C, D and E. ‘C’ is at the height of 10 metres from the ground level. For the viewer ‘A’, the angle of elevation of ‘D’ is double the angle of elevation of ‘C’. The angle of elevation of ‘E’ is triple the angle of elevation of ‘C’ for the same viewer.
Question. Measure of ∠EAB
(a) tan–1 (11)
(b) tan–1 (3)
(c) tan–1 (2/ 11)
(d) tan–1 (11/ 2)
Answer
D
Question. A’ is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between ∠CAB and ∠CA’B is
(a) tan–1 (1/ 12)
(b) tan–1 (1/ 8 )
(c) tan–1 (2/ 5 )
(d) tan–1 (11/ 21)
Answer
A
Question. Measure of ∠CAB =
(a) tan–1(2)
(b) tan–1 (1/ 2 )
(c) tan–1(1)
(d) tan–1(3)
Answer
B
Question. Measure of ∠DAB =
(a) tan–1 3 / 4
(b) tan–1(3)
(c) tan–1 4 /3
(d) tan–1(4)
Answer
C
Read the given para and answer the following MCQs by choosing the most appropriate option
q Corner points of the feasible region for an LPP are (0, 3), (5, 0), (6, 8), (0, 8). Let Z = 4x – 6y be the objective function. Based on the above information, answer the following uestions:
Question. The minimum value of Z occurs at
(a) (6, 8)
(b) (5, 0)
(c) (0, 3)
(d) (0, 8)
Answer
D
Question. Maximum of Z – Minimum of Z =
(a) 58
(b) 68
(c) 78
(d) 88
Answer
B
Read the given para and answer the following
q If there is a statement involving the natural number n such that
(i) The statement is true for n = 1
(ii) When the statement is true for n = k (where k is some positive integer), then the statement is also true
for n = k + 1. Then, the statement is true for all natural numbers n.
Also, if A is a square matrix of order n, then A2 is defined as AA. In general, Am = AA…A (m times), where m is any positive integer.
Question. If A =[1 0 , 21 ,] then |An|, where n ∈ N, is equal to
(a) 2π
(b) 3π
(c) π
(d) 1
Answer
D
Question. If A is a square matrix such that |A| = 2, then for any positive integer n, |An| is equal to
(a) 0
(b) 2π
(c) 2π
(d) π2
Answer
C
Question. Let A = and An = [aij]3×3 for some positive integer n, then the cofactor of a13 is

(a) an
(b) –an
(c) 2an
(d) 0
Answer
D
Question. If A = [3 /1 , -4 / −1] , then for any positive integer n.
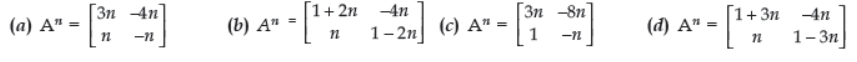
Answer
B