It is important for students to learn Class 10 Maths All Formulas so that they are able to solve all Mathematics questions properly.
On this page, we have provided the Class 10 Mathematics formula for all chapters. You should learn all these formulas so that when you solve mathematics questions you are able to apply these formulas and easily solve all questions. It is important to write the formulas prior to solving the question as it will always help you get extra marks. We have also provided a lot of MCQ Questions for Class 10 Mathematics for the upcoming exams.
Real Numbers Formulas for Class 10
1. HCF (x,y) × LCM (x,y) = xy
2. a = bq + r [dividend = divisor × quotient + remainder]
3. Terminating Expansion : 2, 4, 5, 8
4. Non terminating but repeating : 3, 6, 9, 7
5. (a + b)2 = a2 + 2ab + b2
6. (a – b)2 = a2 – 2ab + b2
7. a2 – b2 = (a + b) (a – b)
8. (x + a) (x + b) = x2 + (a + b)x + ab
9. (a + b)3 = a3 + b3 + 3ab(a + b)
10. (a –b)3 = a3 – b3 – 3ab(a –b)
11. a3 + b3 = (a + b) (a2 – ab +b2)
12. a3 – b3 = (a – b) (a2 + ab + b2)
13. (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
14. a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
15. a3 + b3 + c3 – 3abc = 0 [if a + b + c = 0 or a = b = c]
Polynomials Formulas for Class 10
1. x = a is a zero of polynomial p(x), if p(a) = 0
2. If x = a is a zero of p(x) then (x – a) is a factor of p(x) & vice versa
3. nth degree polynomial has maximum ‘n’ roots.
4. if α & β are roots of ax2 + bx + c = 0 then α + β = -b/a and αβ= c/a
5. Quadratic Equation with α & β as roots is k(x – α) (x – β) = 0
6. If (x – a) and (x – b) are factors of p(x), then (x – a)(x – b) is also a factor of p(x).
7. If graph of a polynomial cuts the x-axis at ‘n’ points then no. of roots of the polynomial are ‘n’.
8. If α, β, γ are roots of ax3 + bx2 + cx + d = 0 then:
α + β + y = -b/a
αβ + βy + yα = c/a
αβy = -d/a
9. Cubic equation with roots α, β, γ is : k [x3 – (α + β + γ)x2 + (αβ + βγ + γα)x – αβγ] = 0.
10. p(x) = g(x). q(x) + r(x). Where g(x) is divisor, q(x) is quotient and r(x) is remainder.
Pair Of Linear Equations Formulas for Class 10
1. ax + by + c = 0 is a linear equation in 2 variables. It represents a straight line in 2D cartesian plane.
2. There are three types of pair of lines :
(i) Intersecting
(ii) Parallel
(iii) Coincident
3. In two given lines : a1x +b1y + c1 = 0
a2x + b2y + c2 = 0
Lines are intersecting if a1/a2 ≠ b1/b2 and they have unique solution.
Lines are parallel if a1/a2 = b1/b2 ≠ c1/c2 and they have no solution.
Lines are coincident if a1/a2 = b1/b2 = c1/c2 and they have infinite solution.
4. Lines a1x + b1y + c1 = 0 & a2x + b2y + c2 = 0 are said to be consistent if they have unique solution or infinite solution.
5. Lines are said to be inconsistent if they have no solution.
6. Graphically, the solution is the intersection point of the two lines.
7. There are 3 methods by which we can solve the equations algebraically:Substitution, Elimination and Cross Multiplication.
8. For questions like upstream, downstream, remember that : d = s × t ie : distance = speed × time.
Coordinate Geometry Formulas for Class 10
1. x-axis and y-axis divide the coordinate plane into 4 quadrants.
2. Each point in cartesian plane a coordinate: (x, y)
3. x-coordinate is called absicca & y-coordinate is called ordinate.
4. First Coordinate: (+, +)
Second Coordinate: (–, +)
Third Coordinate: (–, –)
Fourth Coordinate: (+, –)
5. Distance Formula:
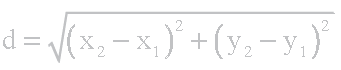
6. Section Formula: a point P divides the line joining A (x1, y1) & B(x2, y2) in ratio m : n, then coordinates of P are :

7. Mid point Formula.

8. If the point P is given, then to find out the ratio, assume the ratio to be k : 1.
Area Related To Circles Formulas for Class 10
1. Circumference of a circle is 2πr.
2. Area of circle is πr2.
3. Area of a sector making angle θ at the center is θ/360 x πr2
4. Length of arc making angle θ at the center is θ/360 x 2πr2
Probability Formulas for Class 10
1. P (E) = no.of favourableoutcomes / no.of totaloutcomes
2. Sample space is the set of total outcomes.
3. Probability of Sure Event is 1.
4. Probability of impossible event is 0.
5. 0 ≤ P(E) ≤ 1
6. E→ is complementary event of E. P(E) + P(E→) = 1.
Trigonometry Formulas for Class 10
1. sinθ = P/h, where p is the side opposite to angle θ and h is the hypotenuse
2. cosθ = P/h, where b is ‘base’ side which is not ‘p’ & ‘h’.
3. tanθ = sinθ/cosθ = P/b
4. sinθ = P/h cosecθ = h/P
cosθ = b/h secθ = h/b
tanθ = P/b cotθ = b/P
5.
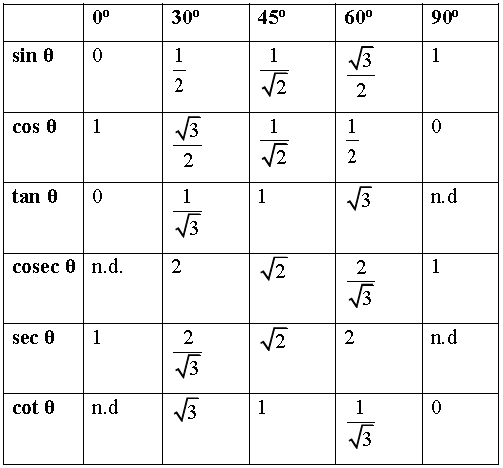
6. sin (90o – θ) = cos θ
cos (90o – θ) = sin θ
7. sec (90o – θ) = cosec θ
cosec (90o – θ) = sec θ
8. tan (90o – θ) = cot θ
cot (90o – θ) = tan θ
9. sin2 θ + cos2 θ = 1
10. sec2 θ – tan2 θ = 1
11. cosec2 θ – cot2 θ = 1
Triangles Formulas for Class 10
1. Two figures are said to be congruent if they are exact copies of each other.
2. Two figures are said to be similar if their shapes are same and dimensions are proportional.
3. Area of triangles

4. Area of a right angled triangles : A = (1/2) bh
5. Area of equilateral triangle : A = (√3/4)a2
6. Basic Proportionality theorem :
If DE is | | to BC of a ΔABC then :

7. SSS similarity :
If in 2 triangles ΔABC & ΔDEF,
AB/DE = BC/EF = AC/DF then the two triangles are similar. ΔABC ~ ΔDEF
8. AAA or AA similarity :
If in 2 triangles ΔABC & ΔDEF, ∠A = ∠D, ∠B = ∠E & ∠C = ∠F, the two triangles are similar. ⇒ ΔABC & ΔDEF
Also if 2 angles are same in two triangles then also the triangles are similar.
9. SAS similarity
If in 2 triangles ΔABC & ΔDEF,
AB/DE = BC/EF = and ∠ABC = ∠DEF
than ΔABC ~ ΔDEF
10. If AL, BM, CN are medians / altitudes /⊥r bisector / ∠bisector of ΔABC and DX, EY, FZ are medians / altitudes /⊥r bisector / ∠bisector of ΔDEF and
ΔABC ~ ΔDEF then ..
AB/DE = BC/EF = AC/DF = AL/DX = BM/EY = CN/FZ
11. If ΔABC ~ ΔDEF
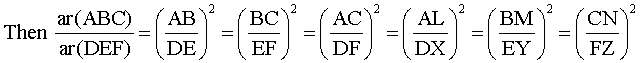
where AL, BM, CN etc. are medians / altitudes /⊥r bisector / ∠bisector.
12. Pythagoras Theorem:
In a ΔABC right angled at B,
AB2 + BC2 = AC2
If BD is ⊥r to AC then the two small right triangles are similar to each other and also to the main ΔABC.


