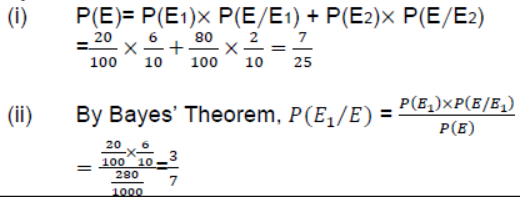Class 12 Mathematics Sample Paper Term 2 With Solutions Set B

Please refer to Class 12 Mathematics Sample Paper Term 2 With Solutions Set B provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Term 2 Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.

Term 2 Sample Paper for Class 12 Mathematics With Solutions Set B

SECTION – A

1. Find:

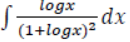
Solution:

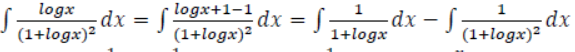
OR

Find:

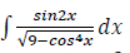
Solution: Put 𝑐𝑜𝑠2𝑥=𝑡⇒−2𝑐𝑜𝑠𝑥𝑠𝑖𝑛𝑥𝑑𝑥=𝑑𝑡⇒𝑠𝑖𝑛2𝑥𝑑𝑥=−𝑑𝑡
The given integral =

2. Write the sum of the order and the degree of the following differential equation: d/dx(dy/dx) = 5
Solution: Order = 2
Degree = 1
Sum = 3

3. If 𝑎̂ and 𝑏̂ aree unit vectors, then prove that |𝑎̂+𝑏̂|=2𝑐𝑜𝑠θ/2 where 𝜃 is the angle between them.
Solution: (𝑎̂+𝑏̂).(𝑎̂+𝑏̂)=|𝑎̂|2+|𝑏̂|²+2(𝑎̂.𝑏̂)
|𝑎̂+𝑏̂|2=1+1+2𝑐𝑜𝑠𝜃 =2(1+𝑐𝑜𝑠𝜃)=4𝑐𝑜𝑠2θ/2
∴|𝑎̂+𝑏̂|=2𝑐𝑜𝑠 θ/2.

4. Find the direction cosines of the following line:

Solution: The given line is

5. A bag contains 1 red and 3 white balls. Find the probability distribution of the number of red balls if 2 balls are drawn at random from the bag one-by-one without replacement.
Solution: Let X be the random variable defined as the number of red balls.
Then X = 0, 1

6. Two cards are drawn at random from a pack of 52 cards one-by-one without replacement. What is the probability of getting first card red and second card Jack?
Solution: The required probability = P((The first is a red jack card and The second is a jack card) or (The first is a red non-jack card and The second is a jack card))

SECTION – B

7. Find:

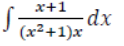
Solution: Let

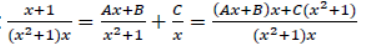
⇒𝑥+1=(𝐴𝑥+𝐵)𝑥+𝐶(𝑥2+1) (An identity)

Equating the coefficients, we get
B = 1, C = 1, A + C = 0
Hence, A = -1, B = 1, C = 1

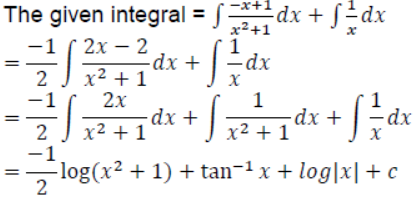
8. Find the general solution of the following differential equation:

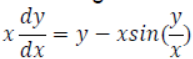
Solution: We have the differential equation:

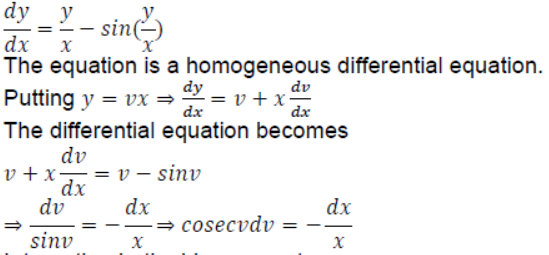
Integrating both sides, we get
𝑙𝑜𝑔|𝑐𝑜𝑠𝑒𝑐𝑣−𝑐𝑜𝑡𝑣|=−𝑙𝑜𝑔|𝑥|+𝑙𝑜𝑔𝐾,𝐾>0 (Here, 𝑙𝑜𝑔𝐾 is an arbitrary constant.)
⇒𝑙𝑜𝑔|(𝑐𝑜𝑠𝑒𝑐𝑣−𝑐𝑜𝑡𝑣)𝑥|=𝑙𝑜𝑔𝐾
⇒|(𝑐𝑜𝑠𝑒𝑐𝑣−𝑐𝑜𝑡𝑣)𝑥|=𝐾 ⇒(𝑐𝑜𝑠𝑒𝑐𝑣−𝑐𝑜𝑡𝑣)𝑥=±𝐾
⇒(𝑐𝑜𝑠𝑒𝑐y/x – cot y/x) 𝑥=𝐶, which is the required general solution.

OR

Find the particular solution of the following differential equation, given that y = 0 when x = π/4 :

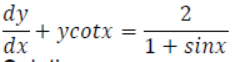
Solution:
The differential equation is a linear differential equation
I F = 𝑒∫𝑐𝑜𝑡𝑥𝑑𝑥=𝑒𝑙𝑜𝑔𝑠𝑖𝑛𝑥=𝑠𝑖𝑛𝑥
The general solution is given by

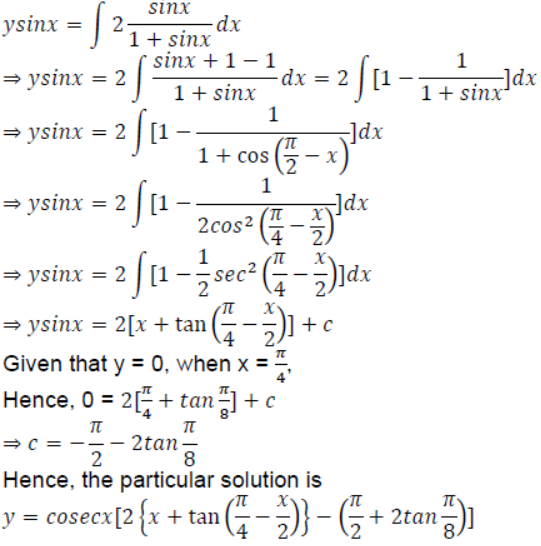
9.

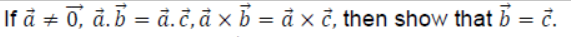
Solution: We have

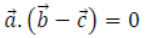
10. Find the shortest distance between the following lines:

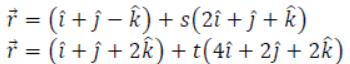
Solution: Here, the lines are parallel. The shortest distance

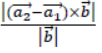
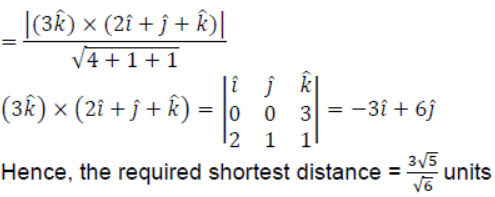
OR

Find the vector and the cartesian equations of the plane containing the point

Solution: Since, the plane is parallel to the given lines, the cross product of

SECTION – C

11. Evaluate:

Solution: The given definite integral =

12. Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y 2 = x and the x-axis.
Solution: Solving x + y = 2 and y 2 = x simultaneously, we get the points of intersection as (1, 1) and (4, -2).

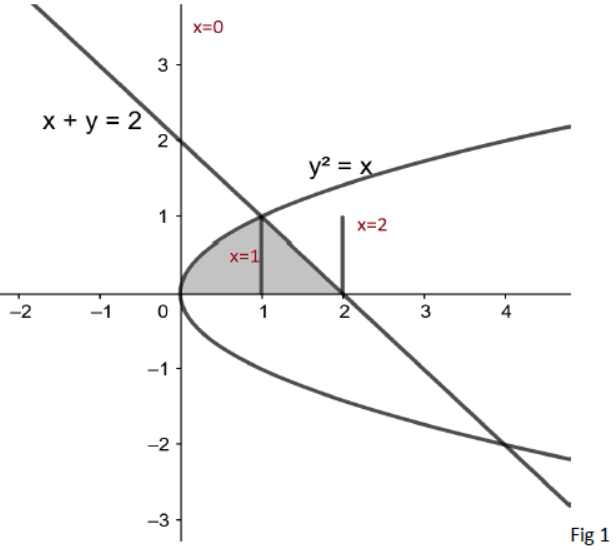
OR

Using integration, find the area of the region: {(𝑥,𝑦):0≤𝑦≤√3𝑥,𝑥2+𝑦2≤4}
Solution: Solving 𝑦=√3𝑥 𝑎𝑛𝑑 𝑥2+𝑦2=4 , we get the points of intersection as (1, √3) and (-1, −√3)

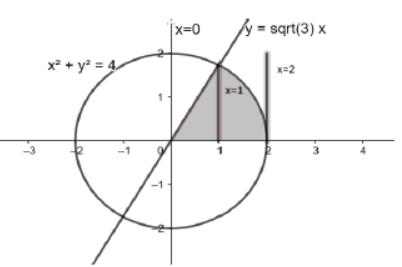
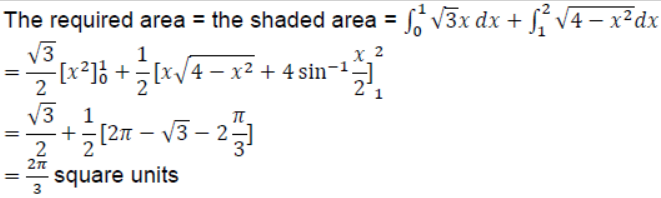
13. Find the foot of the perpendicular from the point (1, 2, 0) upon the plane
x – 3y + 2z = 9. Hence, find the distance of the point (1, 2, 0) from the given plane.
Solution: The equation of the line perpendicular to the plane and passing through the point (1, 2, 0) is

CASE-BASED/DATA-BASED

14.

An insurance company believes that people can be divided into two classes: those who are accident prone and those who are not. The company’s statistics show that an accident-prone person will have an accident at sometime within a fixed one-year period with probability 0.6, whereas this probability is 0.2 for a person who is not accident prone. The company knows that 20 percent of the population is accident prone. Based on the given information, answer the following questions.
(i)what is the probability that a new policyholder will have an accident within a year of purchasing a policy?
(ii) Suppose that a new policyholder has an accident within a year of purchasing a policy. What is the probability that he or she is accident prone?
Solution: Let E1 = The policy holder is accident prone.
E2 = The policy holder is not accident prone.
E = The new policy holder has an accident within a year of purchasing a policy.