Class 12 Mathematics Sample Paper With Solutions Set F

Please refer to Class 12 Mathematics Sample Paper With Solutions Set F provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.

SECTION A

Question numbers 01 to 20 carry 1 mark each.

1. The value of sin⁻¹ (cos 3π/5) is 
(a) π/10
(b) 3π/5
(c) −π/10
(d) −3π/5

2. 

(a) [28]
(b) [24]
(c) 28
(d) 24

3. 

(a) 3
(b) 0
(c) –1
(d) 1

4. 

5. If a .b = 1/2 |a||b|, then the angle between a and b is
(a) 0°
(b) 30° 
(c) 60° 
(d) 90°

6. The two lines x = ay + b, z = cy + d; and x = a’y + b’, z = c’y + d’ are perpendicular to each other, if
(a) a/a’ + c/c’ = 1
(b) a/a’ + c/c’ = −1
(c) aa’ + cc’ =1
(d) aa’+ cc’ = −1

7. The two planes x − 2y + 4z =10 and 18x +17y + kz = 50 are perpendicular, if k is equal to
(a) –4
(b) 4
(c) 2
(d) –2

8. In an LPP, if the objective function z = ax + by has the same maximum value on two corner points of the feasible region, then the number of points at which z_max occurs is
(a) 0
(b) 2
(c) finite
(d) infinite

9. From the set {1, 2, 3, 4, 5}, two numbers a and b ( a ≠ b ) are chosen at random. The probability that a/b is an integer is
(a) 1/3
(b) 1/4
(c) 1/2
(d) 3/5

10. A bag contains 3 white, 4 black and 2 red balls. If 2 balls are drawn at random (without
replacement), then the probability that both the balls are white is
(a) 1/18
(b) 1/36
(c) 1/12
(d) 1/24

Fill in the blanks:
11. If f :R → R be given by f (x) = (3− x³ )^1/3 , then fof (x) = ____________.
Sol. ∴ fof (x) = x . 

12.

Sol. ∴ x.y = −3 .

13. The number of points of discontinuity of f defined by f (x) = x − x +1 is _________.
Sol. Function f (x) is continuous at all real values of x.
So, number of points of discontinuity is zero.

14. The slope of the tangent to the curve y = x³ − x at the point (2, 6) is _________.
Sol. y = x³ − x
⇒ dy/dx = 3x² − 1
∴ dy/dx)_{at (2,6)} = 3 × 2² − 1 = 11 = Slope of tangent

OR

The rate of change of the area of a circle with respect to its radius r, when r = 3 cm, is ______.
Sol. Since area of circle, A = πr²
⇒ dA/dr = 2πr
∴ dA/dr)_{at r=3 cm} = 6π cm² cm^-1.

15. If a̅ is a non-zero vector, then (a̅.î)î + (a̅.ĵ)ĵ+ (a̅.k̂)k̂ equals ______.
Sol. Let a̅ = xî + yĵ+ zk̂
∴ a̅.î = x, a̅.ĵ = y, a̅.k̂ = z
Therefore, (a̅.î)î + (a̅.ĵ)ĵ+ (a̅.k̂ )k̂ = xî + yĵ+ zk̂ = a̅ .

OR

The projection of the vector î − ĵ on the vector î + ĵ is ________.
Sol.

Question numbers 16 to 20 are of very short answer type questions.

16. Find  adj.A, if

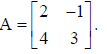
Sol.

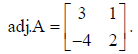
17. Find

Sol.

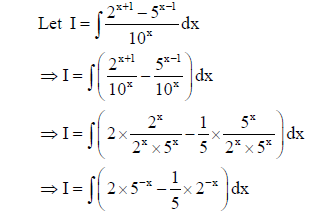
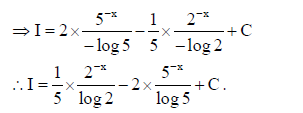
18. Evaluate 

Sol. 

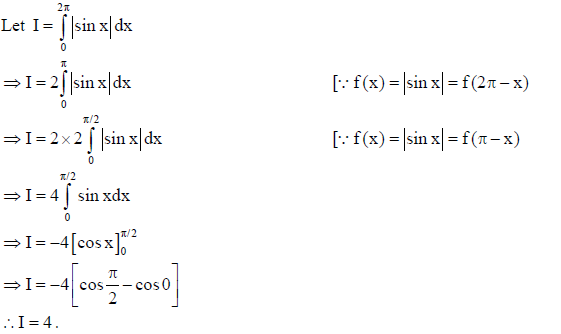
19.

Sol. 

OR

Find ∫dx/√x + x.
Sol.

20. Show that the function y = ax + 2a² is a solution of the differential equation
2 (dy/dx)² + x (dy/dx) − y = 0
Sol. We have y = ax + 2a²     …(i)
⇒ dy/dx = a
Replacing value of ‘a’ in (i), we get : y = (dy/dx)x + 2 (dy/dx)²
That is, 2 (dy/dx)² + x (dy/dx) − y = 0.
Hence, y = ax + 2a² is a solution of the D.E. 2 (dy/dx)² + x (dy/dx) − y = 0.

SECTION B

Question numbers 21 to 26 carry 2 marks each.

21. Check if the relation R on the set A = {1, 2,3, 4,5,6} defined as R = {(x, y) : y is divisible by x} is (i) symmetric (ii) transitive.
Sol. Here R :A→A, A = {1, 2,3, 4,5,6}, R = {(x, y) : y is divisible by x}.
(i) Note that (1,2)∈R but (2,1)∉R .
As 2 is divisible by 1. But 1 isn’t divisible by 2.
So, R isn’t symmetric.
(ii) Since (x, y)∈ R and (y, z) ∈ R implies (x, z)∈R where x, y, z ∈ A therefore, R is a transitive relation.

OR

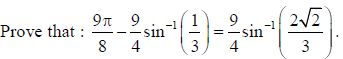
Sol.

22. Find the value of dy/dx at θ = π/3, if x = cosθ− cos 2θ, y = sin θ −sin 2θ.
Sol. x = cosθ− cos 2θ, y = sin θ −sin 2θ

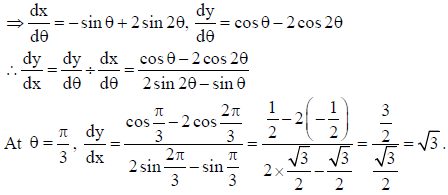
23. Show that the function f defined by f (x) = (x −1)e^x +1 is an increasing function for all x > 0 .
Sol. f (x) = (x −1)e^x +1
⇒ f ‘(x) = (x −1)e^x + e^x
⇒ f ‘(x) = xe^x − e^x + e^x = xe^x
As x > 0 so, f ‘(x) > 0                                     [∴ x > 0 ∴ e^x > 0 and, xe^x > 0
So, function f is an increasing function for all x > 0 .

24. Find |a̅| and |b̅|, if |a̅| = 2|b̅| and (a̅ + b̅).(a̅ − b̅) =12
Sol. Here (a̅ + b̅).(a̅ − b̅) =12
⇒ |a̅|² − a̅.b̅ + b̅.a̅ − |b̅|² =12
⇒ 4 |b̅|² − |b̅|² =12
⇒ |b̅|² = 4
∴ |b̅| = 2
Therefore, |a̅| = 4 and |b̅|= 2

OR

Find the unit vector perpendicular to each of the vectors a̅ = 4î + 3ĵ+ k̂ and b = 2î − ĵ+ 2k̂
Sol. 

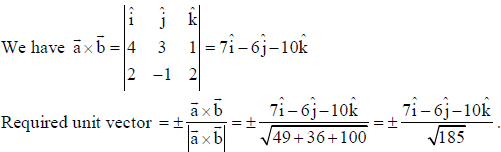
25. Find the equation of the plane with intercept 3 on the y-axis and parallel to xz-plane.
Sol. Required plane makes an intercept of 3 on y-axis so, the plane passes through (0, 3, 0). Also it
is parallel to xz-plane means, the plane is perpendicular to y-axis. Therefore, the y-axis may act as the normal to the plane. So, the d.r.’s of normal to the plane are 0, 1, 0.
The equation of plane is : 0(x − 0) +1(y − 3) + 0(z − 0) = 0 i.e., y −3 = 0 .

26. Find [P(B| A) + P(A| B)], if P(A) = 3/10 , P(B) = 2/5 and P(A ∪ B) = 3/5.
Sol.

SECTION C

Question numbers 27 to 32 carry 4 marks each.

27. Prove that the relation R on Z, defined by R = {(x, y) : (x − y) is divisible by 5} is an
equivalence relation.
Sol. Here R = {(x, y) : (x − y) is divisible by 5} is defined on set of integers Z.
Reflexivity : As x − x = 0 is divisible by 5 ∀ x ∈ Z.
∴ (x, x) ∈ R .
Therefore, R is reflexive.
Symmetry : Let (x, y)∈ R for all x,y ∈ Z. It implies x − y is divisible by 5 .
This further implies, y − x is also divisible by 5 .
So, (y, x) ∈ R .
Therefore, R is symmetric.
Transitivity : Let (x, y)∈R and (y, z) ∈ R ∀ x,y,z ∈ Z.
It implies x − y is divisible by 5 and y − z is divisible by 5.
This further implies, (x − y) + (y − z) = x − z is also divisible by 5.
So, (x, z)∈ R .
Therefore, R is transitive.
Hence, R is an equivalence relation.

28. 

Sol.

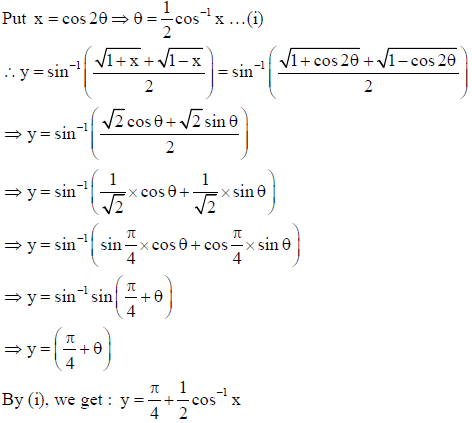
OR

Verify the Rolle’s Theorem for the function f (x) = e^x cos x in [−π/2,π/2].
Sol. 

29. Evaluate :

Sol.

30. For the differential equation given below, find a particular solution satisfying the given condition 
(x + 1) dy/dx =  2e ^−y + 1; y = 0 when x = 0 
Sol. 

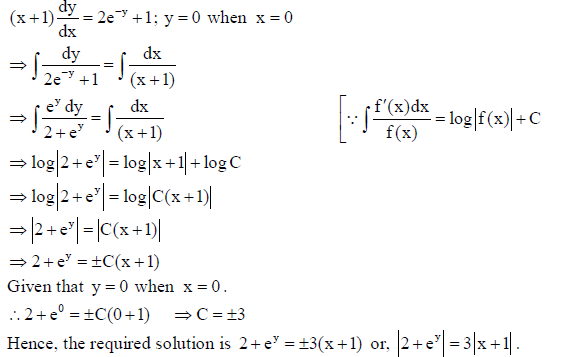
31. A manufacturer has three machines I, II and III installed in his factory. Machine I and II are capable of being operated for at most 12 hours whereas machine III must be operated for at least 5 hours a day. He produces only two items M and N each requiring the use of all the three machines.
The number of hours required for producing 1 unit of M and N on three machines are given in
the following table :

He makes a profit of `600 and `400 on one unit of items M and N respectively. How many
units of each item should he produce so as to maximize his profit assuming that he can sell all
the items that he produced? What will be the maximum profit?
Sol. Let the number of items M and, N be x and y, respectively. 

32. A coin is biased so that the head is three times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails. Hence find the mean of the number of tails.
Sol. Let p = probability of getting tail, q = probability of getting head on the coin.
Since q = 3p so, using p + q =1 we have : p + 3p =1

OR

Suppose that 5 men out of 100 and 25 women out of 1000 are good orators. Assuming that there are equal number of men and women, find the probability of choosing a good orator.
Sol. Let A : a good orator is chosen, E₁ : a man is chosen, E₂ : a woman is chosen.  

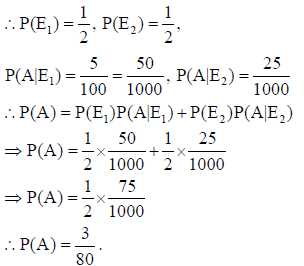
SECTION D

Question numbers 33 to 36 carry 6 marks each.

33. Using properties of determinants, prove that :

Sol.

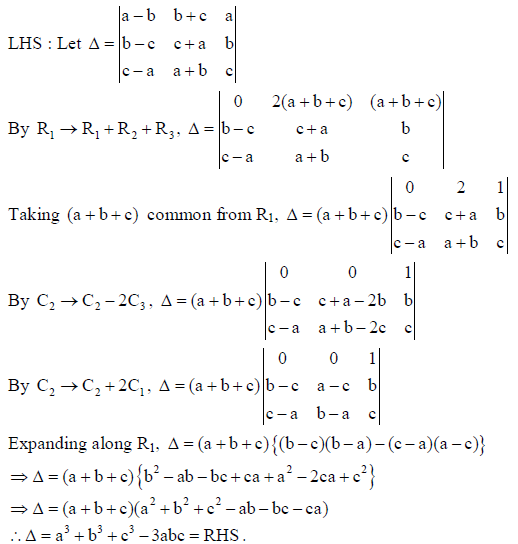
OR

then show that A³ − 4A² − 3A+11 I = O. Hence find A^–1.
Sol. 

34. Find the intervals on which the function f (x) = (x −1)³ (x − 2)² is (a) strictly increasing
(b) strictly decreasing.
Sol. We have f (x) = (x −1)³ (x − 2)²
⇒ f ‘(x) = (x −1)³ × 2(x − 2) + (x − 2)² ×3(x −1)²
⇒ f ‘(x) = (x −1)² (x − 2){2(x −1) + 3(x − 2)}
⇒ f ‘(x) = (x −1)² (x − 2)(5x −8)
For f ‘(x) = (x −1)² (x − 2)(5x −8) = 0
Either (x −1)² = 0 or, (x − 2) = 0 or, (5x −8) = 0
∴ x =1, 2, 8/5

Hence, f (x) is (a) strictly increasing in x ∈ (−∞ , 1) ∪ (1, 8/5) ∪ (2,∞) and (b) strictly decreasing in x ∈ (8/5 , 2).

OR

Find the dimension of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its side. Also find the maximum volume. 
Sol. Let l and b represent the length of rectangle and its width respectively.
So, 2(l + b) = 36
⇒ l + b = 18…(i)
If rectangle is revolved about its length to form a cylinder then, radius of the base of cylinder
r = b and height h = l.
Now volume of cylinder, V = πr²h
⇒ V = πb² (18− b) = π(18b² − b³ )
∴ dV/db = π (36b − 3b² ) = 3π (12b b² )
and, d²V/db² = 3π (12− 2b) = 6π (6−b)
For critical points, dV/db = 0
⇒ 3π(12b − b² ) = 0
⇒ b(12 − b) = 0       [ b ≠ 0
⇒ b =12,
∴ l = 6                     [By (i)
 d²V/db²]_{at b=12} = 36π < 0
So, V is maximum at b =12 cm.
Hence, l = 6 cm, b =12 cm are the dimensions of rectangle.
And, maximum volume V = π(12)² (18 −12) = 864π cm³ .

35. Find the area of the region lying in the first quadrant and enclosed by the x-axis, the line y = x and the circle x² + y² = 32 .
Sol. We’ve x² + y² = 32…(i),

36. Show that the lines r̅ = a̅ + λb̅  and r̅ = b̅ + μa̅  are coplanar and the plane containing them is given by r̅.(a̅ × b̅) = 0
Sol. 

Now normal to the plane containing the coplanar lines can be obtained by b̅₁ × b̅₂ = b̅ × a̅
(That is, cross product of vectors parallel to the given lines will give the normal vector).
Hence the equation of required plane, whose normal is given by b̅ × a̅ and which contains the
points with position vector a̅ and b̅  (we need any one point) is :