Please refer to Class 12 Mathematics Sample Paper With Solutions Set O provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
1.
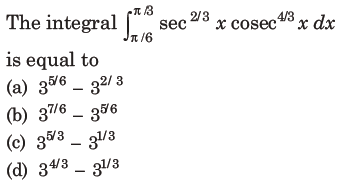
Answer
B
2. The sum of series
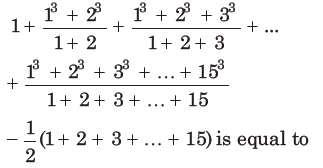
(a) 620
(b) 660
(c) 1240
(d) 1860
Answer
A
3. The area (in sq units) of the region bounded by the curves y = 2x and y =|x + 1|, in the first quadrant is
(a)3/2
(b) loge 2+3/2
(c)1/2
(d)3/2-1/-loge2
Answer
D
4. If 5x + 9 = 0 is the directrix of the hyperbola 16X2-9Y2=144, then its corresponding focus is
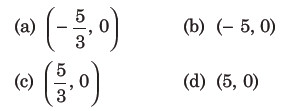
Answer
B
5. The locus of the centres of the circles, which touch the circle, x2+Y2= 1 externally, also touch the Y-axis and lie in the first quadrant, is
(a) y = √1 + 2x, x ≥ 0
(b) y = √1 + 4x, x ≥ 0
(c) x = √1 + 2y, y ≥ 0
(d) x = √1 + 4y, y ≥ 0
Answer
A
6. The tangent and normal to the ellipse 3x2+ 5y2 = 32 at the point P(2, 2) meets the X-axis at Q and R,respectively. Then, the area (in sq units) of the Δ PQR is
(a)16/3
(b)14/3
(c)34/15
(d)68/15
Answer
D
7 If the tangent to the curve y=x/x2-3‘

line 2x + 6y – 11 = 0, then
(a) |6a + 2b|= 19
(b) |6a + 2b|= 9
(c) |2a + 6b|= 19
(d) |2a + 6b|= 11
Answer
A
8.
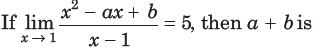
equal to
(a) – 4
(b) 1
(c) – 7
(d) 5
Answer
C
9. Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is
(a) 180
(b) 210
(c) 170
(d) 190
Answer
C
10. Letλ be a real number for which the system of linear equations x + y + z = 6, 4x + λy – λz = λ – 2 and 3x + 2y – 4z = – 5 has infinitely many solutions. Then λ is a root of the quadratic equation
(a) λ2 l – 3 – 4 = 0
(b) λ2 l + 3λ – 4 = 0
(c) λ2 -λ – 6 = 0
(d) λ2+ λ – 6 = 0
Answer
C
11. The angles A, B and C of a Δ ABC are in AP and a : b = 1: √3. If c = 4 cm, then the area (in sq cm) of this triangle is
(a)√2/3
(b) 4√3
(c) 2√3
(d)4/√3
Answer
C
12. The distance of the point having position vector
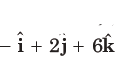
from the straight line passing through the point (2, 3, – 4) and parallel to the vector,
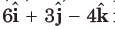
is
(a) 2 √13
(b) 4 √3
(c) 6
(d) 7
Answer
D
13.
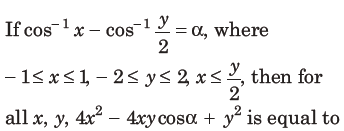
(a) 2 sin2 α
(b) 4 cos2α a+ 2x2Y2
(c) 4 sin2 α
(d) 4 sin2α -2X2Y2
Answer
C
14. If both the mean and the standard deviation of 50 observations x1,x2,…,x50 are equal to 16, then the mean of (x1-4)2,(x2-4)2,…,(x50-4)2is
(a) 480
(b) 400
(c) 380
(d) 525
Answer
B
15. If the plane 2x – y + 2z + 3 = 0 has the distances1/3 and 2/3 units from the planes 4x – 2y + 4z +λ = 0 and 2x – y + 2z + µ = 0, respectively, then the maximum value of λ + μ is equal to
(a) 13
(b) 15
(c) 5
(d) 9
Answer
A
16 The sum of the real roots of the
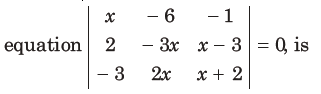
(a) 0
(b) – 4
(c) 6
(d) 1
Answer
A
17. Lines are drawn parallel to the line 4x – 3y + 2 = 0, at a distance 3/5 from the origin. Then which one of the following points lies on any of these lines?
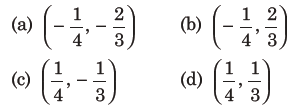
Answer
B
18. A perpendicular is drawn from a point on the line x – 1/2=y+1/-1=z/1 to the plane x + y + z = 3 such that the foot of the perpendicular Q also lies on the plane x – y + z = 3. Then, the coordinates ofQ are
(a) (- 1, 0, 4)
(b) (4, 0, – 1)
(c) (2, 0, 1)
(d) (1, 0, 2)
Answer
C
19.
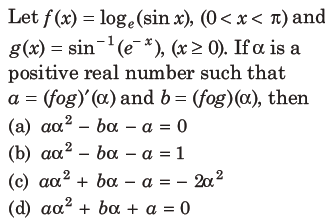
Answer
B
20. If the line ax + y = c, touches both the curves x2+y2=1 = and y2=4 √2x, then |c|is equal to
(a)1/√2
(b) 2
(c) √2
(d)1/2
Answer
C
21.

is a constant of integration, then g (- 1) is equal to
(a) – 1
(b) 1
(c) – 1/2
(d) – 5/2
Answer
D
22. Let a1,a2,a3,.. be an AP with a6 = 2.
Then, the common difference of this AP, which maximises the product a1,a4,a5, is
(a)8/5
(b)2/3
(c)3/2
(d)6/5
Answer
A
23. If z and w are two complex numbers such that|zw|= 1 and arg(z) – arg(w) = π/2 , then
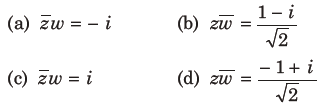
Answer
A
24. A spherical iron ball of radius 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm3 /min. When the thickness of the ice is 5 cm, then the rate at which the thickness (in cm/min) of the ice decreases, is
(a)1/9 π
(b)1/18 π
(c)1/36 π
(d)5/6 π
Answer
B
25. The negation of the boolean expression ~ s v (~ r ∧ s) is equivalent to
(a) s ∧ r
(b) ~ s ∧ ~ r
(c) s v r
(d) r
Answer
A
26. Minimum number of times a fair coin must be tossed so that the probability of getting atleast one head is more than 99% is
(a) 8
(b) 6
(c) 7
(d) 5
Answer
C
27. The smallest natural number n, such that the coefficient of x in the expansion of
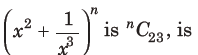
(a) 35
(b) 23
(c) 58
(d) 38
Answer
D
28. The number of real roots of the equation
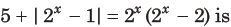
(a) 1
(b) 3
(c) 4
(d) 2
Answer
A
29. Let y = y(x) be the solution of the differential equation,
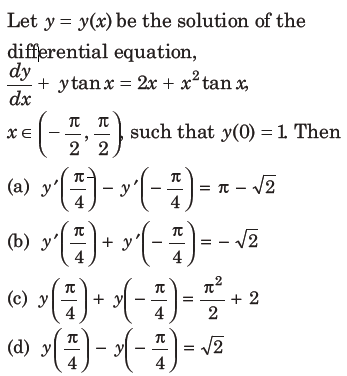
Answer
A
30. Let a, b and c be in GP with common ≠ <≤1/2 3a, 7b and 15c are the first three terms of an AP, then the 4th term of this AP is
(a) 5 a
(b)2/3 a
(c) a
(d)7/3 a
Answer
C
