Continuity and Differentiability Class 12 Mathematics Important Questions

Students can read the important questions given below for Continuity and Differentiability Class 12 Mathematics. All Continuity and Differentiability Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.

Important Questions of Continuity and Differentiability Class 12

Very Short Answer Type Questions

Question. Determine the value of the constant ‘k’ so that

Answer.

Question. Determine the value of ‘k’ for which the following function is continuous at x = 3 :

Answer.

Short Answer Type Questions-I

Question. Find the value of k for which the function f (x)

Answer.

Question.

Answer.

Question. Find the value of c in Rolle’s theorem for the function f (x) = x³ – 3x in [– √3 , 0].
Answer. If f (x) = x³ – 3x [– √3 , 0]
(i) Since f (x) being a polynomial function, it is continuous in [– √3 , 0].
(ii) f (x) = 3x² – 3, which exists in (– 3 , 0).
(iii) f (– √3 ) = (– √3 )³ – 3(– √3)
= –3 √3 + 3 √3 = 0
f (0) = (0)³ – 3(0) = 0
f(c) = 0

Short Answer Type Questions-II

Question. If y = cosec–1 x, x > 1, then show that

Answer. 1^st method y = cosec^–1 x
Differentiating both sides w.r.t. x, we have

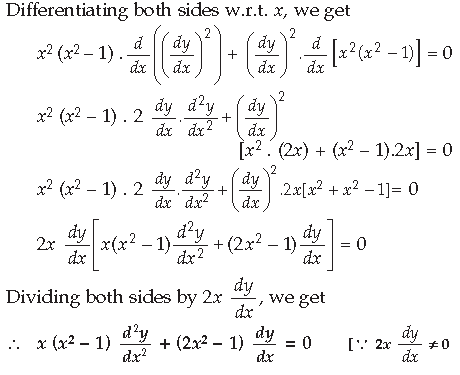
Question. Find the relationship between ‘a’ and ‘b’ so that the function ‘f ’ defined by

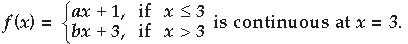
Answer.

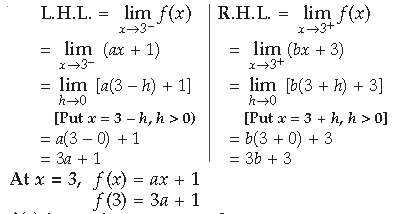
f (x) is continuous at x = 3
∴ L.H.L. = R.H.L. = f (3)
3a + 1 = 3b + 3 = 3a + 1
3a + 1 = 3b + 3
∴ 3a – 3b = 2 is the required relationship between a and b.

Question. Find the value of k so that the function f, defined by

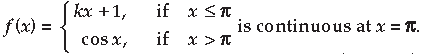
Answer.

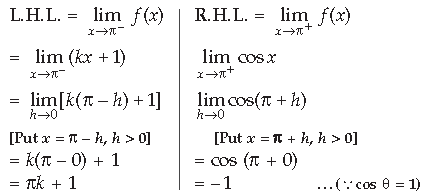
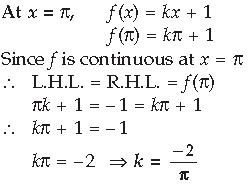
Question. For what value of λ is the function

Answer.

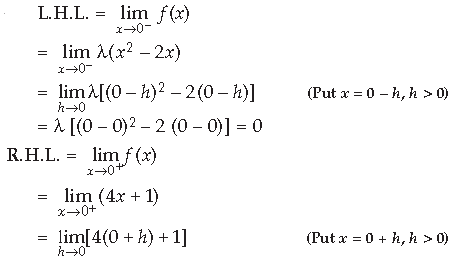
= 4 (0 + 0) + 1 = 1
At x = 0, f (x) = λ (x2 – 2x)
f (0) = λ (0 – 0) = 0
Since f is continuous at x = 0 (given)
L.H.L. = R.H.L. = f (0)
0 = 1 = 0, Which is not possible
∴ For no value of λ, f is continuous at x = 0.

Question. Discuss the continuity of the function

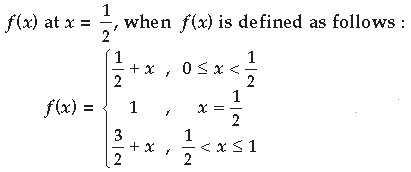
Answer.

Question.

Answer.

Question.

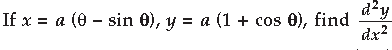
Answer.

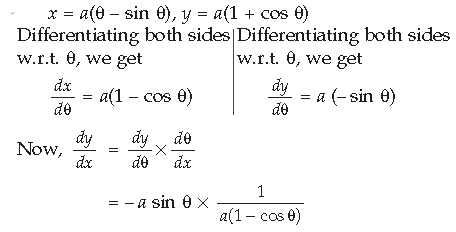
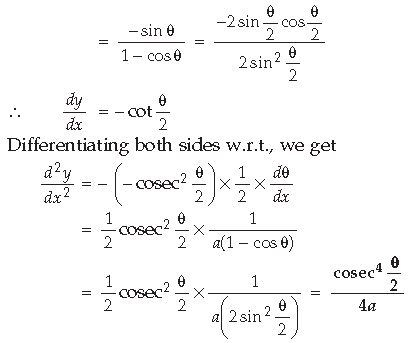
Question.

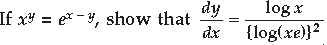
Answer. x^y = e^x–y
Taking log on both sides, we get
y log x = (x – y) log e
⇒ y log x = x – y                      [ ∵ log e= 1]
⇒y + y log x = x

Question.

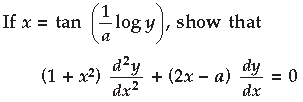
Answer.

Question. Prove that :

Answer.

Question.

Answer.

Question.

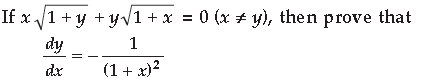
Answer.

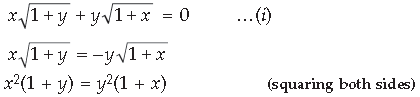
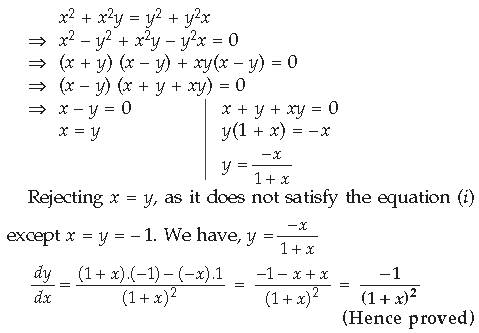
Question. If x = a(θ – sin θ) and y = a (1 + cos θ), find.

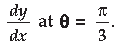
Answer. x = a(θ – sin θ)
Differentiating both sides w.r.t. θ, we get

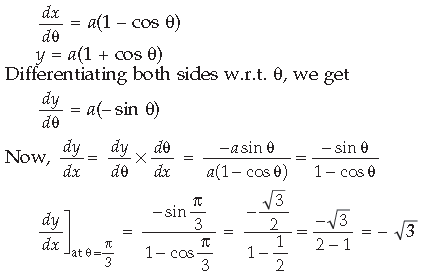
Question.

Answer.

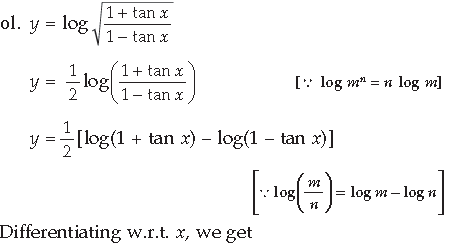
Question. If y = a sin x + b cos x, prove that
Answer. y = a sin x + b cos x

(a sin x + b cos x)² + (a cos x – b sin x)²
= a² sin² x + b² cos² x + 2ab sin x cos x
+ a² cos² x + b² sin² x – 2ab sin x cos x
= a² (sin² x + cos² x) + b² (sin² x + cos² x)
= a² (1) + b² (1)
= a² + b² = R.H.S.

Question.

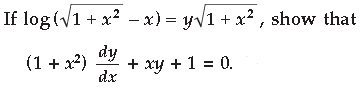
Answer.

Question.

Answer.

Question. If x = a sin 2t (1 + cos 2t) and

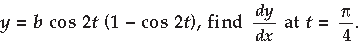
Answer. x = a sin 2t (1 + cos 2t)
Differentiating w.r.t. t, we get

Question.

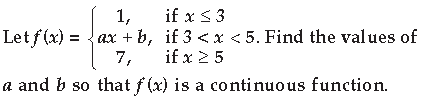
Answer.

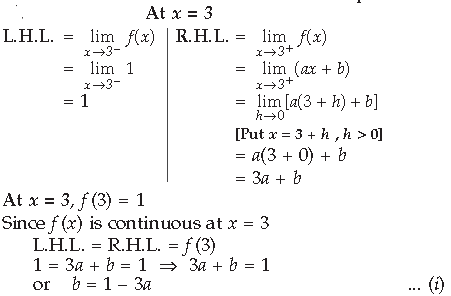
Question. Find the value of k so that the following function is continuous at x = 2

Answer.

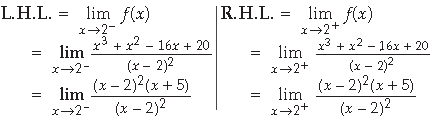
Question. Find the value of k so that the function f is continuous at x = π/2 :

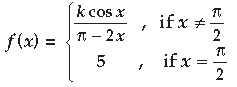
Answer.

Question. Prove that the function f given by f (x) = |x – 3|, x ∈ R is continuous but not differentiable at x = 3.
Answer.

Question. If (cos x)^y = (cos y)^x, find dy/dx
Answer. (cos x)^y = (cos y)^x
Taking log on both sides, we have
y. log cos x = x. log cos y
Differentiating both sides w.r.t. x, we have

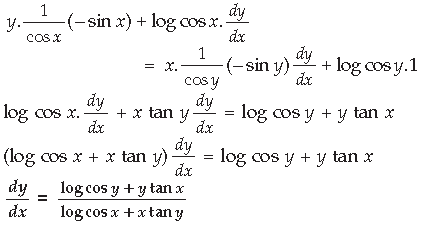
Question. If y = (tan^–1 x)², show that

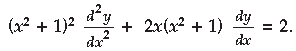
Answer. y = (tan^–1 x)²

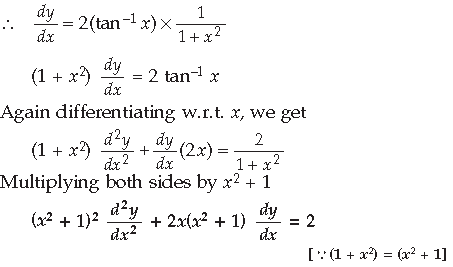
Question. If y = sin^–1 x, show that

Answer. y = sin^–1 x

Question. If x = a(cos t + t sin t) and y = a (sin t – t cos t), 0

Answer. x = a(cos t + t sin t)
Differentiating w.r.t. t

,

Question.

Answer. Part I : y = a sin t
Differentiating both sides w.r.t. t, we get

Question.

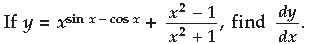
Answer.

Question.

Answer.

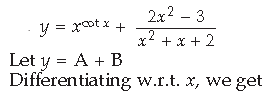
Question.

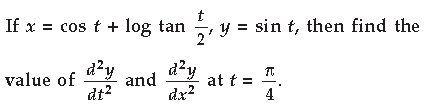
Answer.

Question. Find the value of k, for which

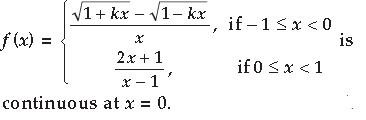
Answer.

Question. Differentiate the following function with respect to x :
(log x)^x + x^log x
Answer. Let y = (log x)^x + x^log x
Let y = A + B
Differentiating w.r.t. x, we get

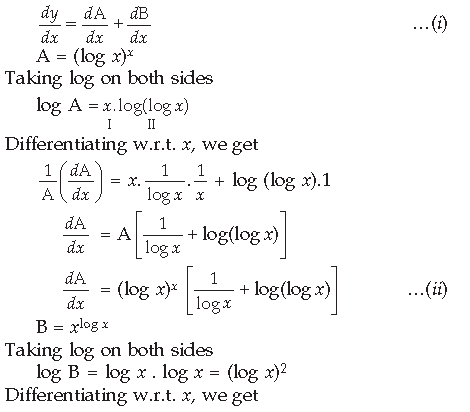
Question. If x = a sin t and y = a(cos t + log tan ^t/₂), find d²y/dx²
Answer. x = a sin t
Differentiating both sides w.r.t.,t we get

Question.

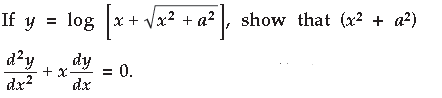
Answer.

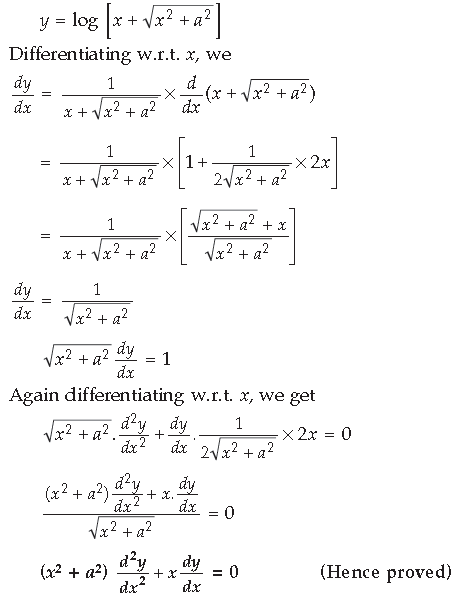
Question.

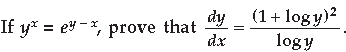
Answer. y^x = e^y–x
Taking log on both sides
x log y = (y – x).log e
x log y = y – x                         [ ∵ log e = 1
x + x log y = y
x(1 + log y) = y

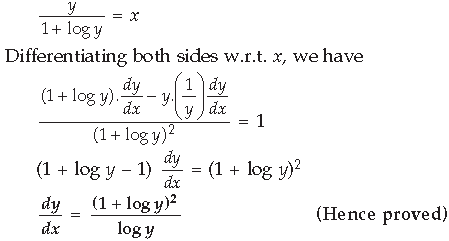
Question. Differentiate the following with respect to x :

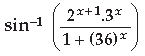
Answer.

Question.

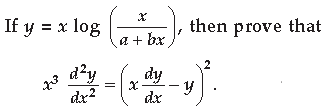
Answer.

Question. If x sin (a + y) + sin a cos (a + y) = 0, prove that

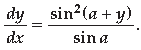
Answer. x sin(a + y) + sin a cos(a + y) = 0
sin a . cos(a + y) = – x sin(a + y

Question. If x = a cos θ + b sin θ and y = a sin θ – b cos θ, then prove that

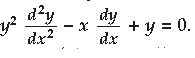
Answer.

Question.

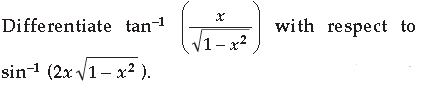
Answer.

Question.

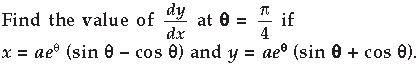
Answer. x = ae^θ (sin θ – cos θ) …(given)
Differentiating both sides w.r.t. θ, we get

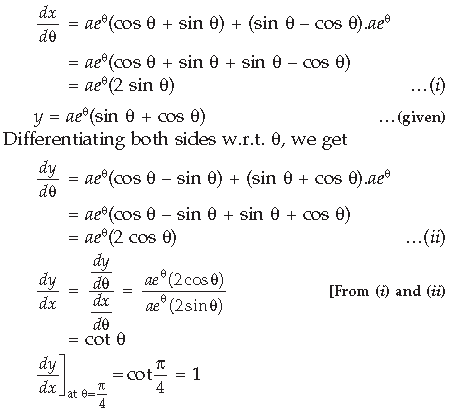
Question. If x = cos t(3 – 2 cos² t) and y = sin t (3 – 2 sin² t), find the value of

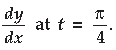
Answer.

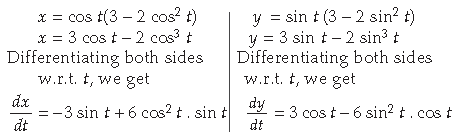
Question. If x = a(cos t + t sin t) and y = a(sin t – t cos t), then find the value of

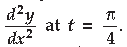
Answer.

Question. If y = Pe^ax + Qe^bx, show that

Answer. y = Pe^ax + Qe^bx                            …(i)
Differentiating both sides w.r.t. x, we get

Question.

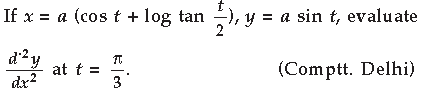
Answer.

Question.

Answer.

Question. If (tan^–1 x)y + y^cot x = 1, then find dy/dx
Answer. Let A = (tan^–1 x)^y
Taking log on both sides
log A = y (log tan^–1x)
Differentiating both sides w.r.t. x

Question. Show that the function f(x) = |x – 1| + |x + 1| for all x ∈ R, is not differentiable at the points x = – 1 and x = 1.
Answer.

Question. For what value of λ the function defined by

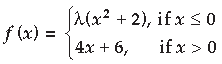
is continuous at x = 0?
Hence check the differentiability of f(x) at x = 0.
Answer. Value of & when f(x) is continuous at x = 0

Question.

Answer.

109. If y = e^{m sin−1} , then show that
Answer. y = e^{m sin−1}
Differentiating both sides w.r.t. x, we get

Question.

Answer.

CASE STUDY :

A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + | x-2|, where f(x) represents the height of the pot.

Question. When x > 4 What will be the height in terms of x ?
a. x – 2
b. x -3
c. 2x -5
d. 5 – 2x

Question. Will the slope vary with x value?
a. Yes
b. No

Question. What is 𝑑𝑦/𝑑𝑥 at x = 3
a. 2
b. -2
c. Function is not differentiable
d. 1

Question. When the x value lies between (2,3) then the function is
a. 2x -5
b. 5 – 2x
c. 1
d. 5

Question. If the potter is trying to make a pot using the function f(x) = [x] ,will he get a pot or not? Why?
a. Yes, because it is a continuous function
b. Yes, because it is not continuous
c. No , because it is a continuous function
d. No , because it is not continuous