Please refer to Laws of Motion Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Laws of Motion Notes and Questions
Newton’ 1st law or Law of Inertia
Every body continues to be in its state of rest or of uniform motion until and unless and until it is compelled by an external force to change its state of rest or of uniform motion.
Inertia
The property by virtue of which a body opposes any change in its state of rest or of uniform motion is known as inertia. Greater the mass of the body greater is the inertia. That is mass is the measure of the inertia of the body.
Numerical Application
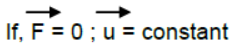
Physical Application
1. When a moving bus suddenly stops, passenger’s head gets jerked in the forward direction.
2. When a stationery bus suddenly starts moving passenger’s head gets jerked in the backward direction.
3. On hitting used mattress by a stick, dust particles come out of it.
4. In order to catch a moving bus safely we must run forward in the direction of motion of bus.
5. Whenever it is required to jump off a moving bus, we must always run for a short distance after jumping on road to prevent us from falling in the forward direction.
Key Concept
In the absence of external applied force velocity of body remains unchanged.
Newton’ 2nd law
Rate of change of momentum is directly proportional to the applied force and this change always takes place in the direction of the applied force.
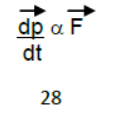

Note :- Above result is not Newton’s second law rather it is the conditional result obtained from it, under the condition when m = constant.
Numerical Application
Physical Application
Horizontal Plane
i) Case – 1 N
Body kept on horizontal plane is at rest.
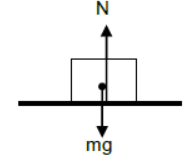
For vertical direction
N = mg(since body is at rest)
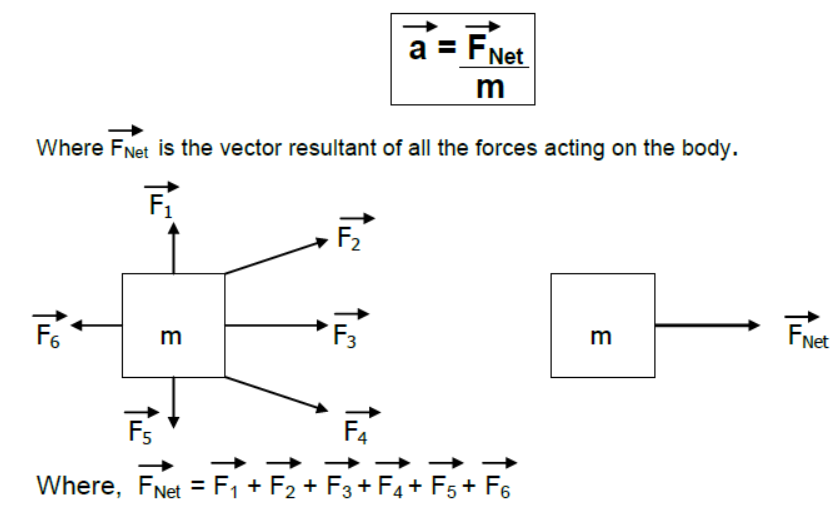
ii) Body kept on horizontal plane is accelerating horizontally under single horizontal force.
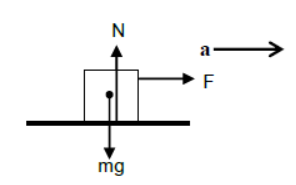
For vertical direction
N = mg (since body is at rest)
For horizontal direction
F = ma mg
iii) Body kept on horizontal plane is accelerating horizontally towards right under two horizontal forces. (F1 > F2)
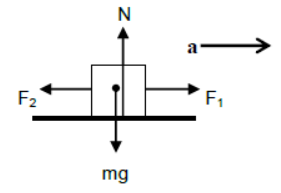
For vertical direction
N = mg (since body is at rest)
For horizontal direction
F1 – F2 = ma
iv) Body kept on horizontal plane is accelerating horizontally under single inclined force
For vertical direction
N + FSinθ = mg (since body is at rest)
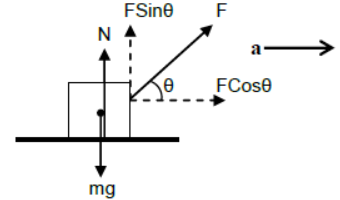
For horizontal direction
FCosθ = ma
v) Body kept on horizontal plane is accelerating horizontally towards right under an inclined force and a horizontal force.
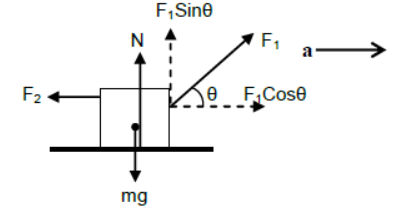
For vertical direction
N + F1Sinθ = mg (since body is at rest)
For horizontal direction
F1Cosθ – F2 = ma
vi) Body kept on horizontal plane is accelerating horizontally towards right under two inclined forces acting on opposite sides.
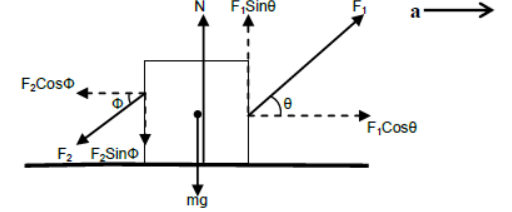
For vertical direction
N + F1Sinθ = mg + F2 SinФ
(since body is at rest)
For horizontal direction
F1Cosθ – F2CosФ = ma
Inclined Plane
i) Case – 1
Body sliding freely on inclined plane.
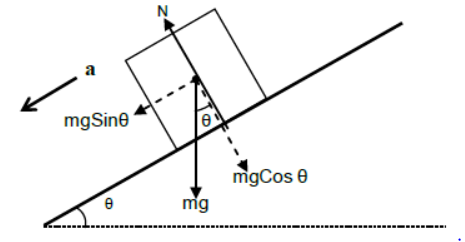
Perpendicular to the plane
N = mgCosθ (since body is at rest)
Parallel to the plane
mgSinθ = ma
ii) Case – 2
Body pulled parallel to the inclined plane.
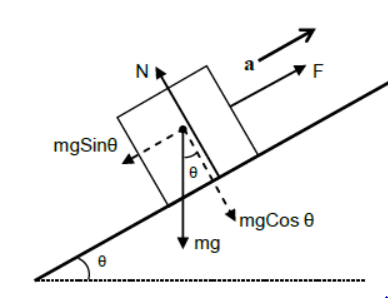
Perpendicular to the plane
N = mgCosθ (since body is at rest)
Parallel to the plane
F – mgSinθ = ma
iii) Case – 3
Body pulled parallel to the inclined plane but accelerating downwards.
Perpendicular to the plane
N = mgCosθ (since body is at rest)
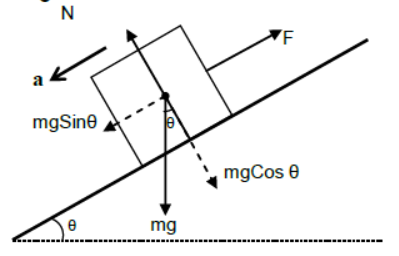
Parallel to the plane
mgSinθ – F = ma
iv) Case – 4
Body accelerating up the incline under the effect of two forces acting parallel to the incline.
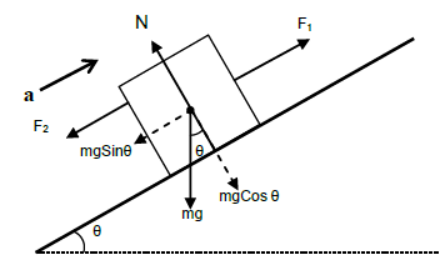
Perpendicular to the plane
N = mgCosθ (since body is at rest)
Parallel to the plane
F1 – F2 – mgSinθ = ma
v) Case – 5
Body accelerating up the incline under the effect of horizontal force.
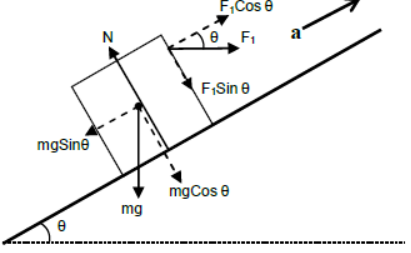
Perpendicular to the plane
N = mgCosθ + F1Sinθ (since body is at rest)
Parallel to the plane
F1Cosθ – mgSinθ = ma
vi) Case – 6
Body accelerating down the incline under the effect of horizontal force and gravity.
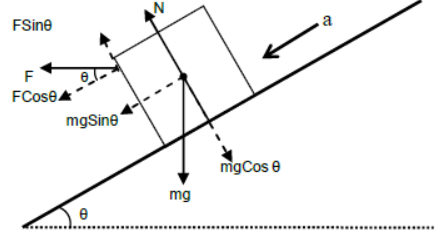
Perpendicular to the plane
N + FSinθ = mgCosθ (since body is at rest)
Parallel to the plane
FCosθ + mgSinθ = ma
vii) Case – 7
Body accelerating up the incline under the effect of two horizontal forces acting on opposite sides of a body and gravity.
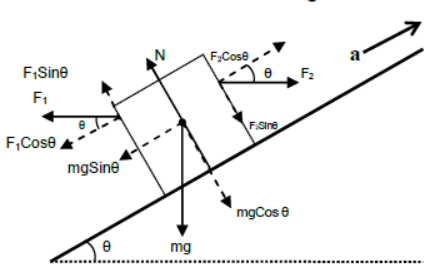
Perpendicular to the plane
N + F1Sinθ = mgCosθ + F2Sinθ(since body is at rest)
Parallel to the plane
F2Cosθ – F1Cosθ – mgSinθ = ma
Vertical Plane
i) Case – 1
Body pushed against the vertical plane by horizontal force and moving vertically downward.
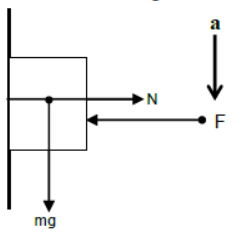
For horizontal direction
mg = ma (since body is at rest)
For vertical direction
F = N
ii) Case – 2
Body pushed against the vertical plane by horizontal force and pulled vertically upward.
For vertical direction
F2 – mg = ma
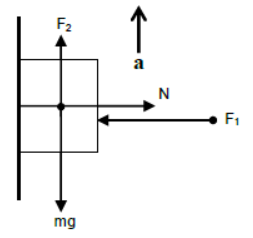
For horizontal direction (since body is at rest)
N = F1
iii) Case – 3
Body pushed against the vertical plane by inclined force and accelerates vertically upward.
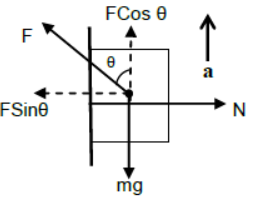
For horizontal direction
N = FSinθ (since body is at rest)
For vertical direction
FCosθ – mg = ma
iv) Case – 3
Body pushed against the vertical plane by inclined force and accelerates vertically downward.
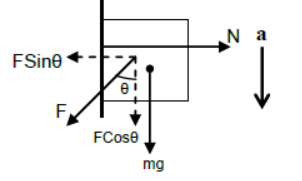
For horizontal direction
N = FSinθ (since body is at rest)
For vertical direction
FCosθ + mg = ma
Tension In A Light String
Force applied by any linear object such as string, rope, chain, rod etc. is known as it’s tension. Since string is a highly flexible object so it can only pull the object and can never push. Hence tension of the string always acts away from the body to which it is attached irrespective of the direction.
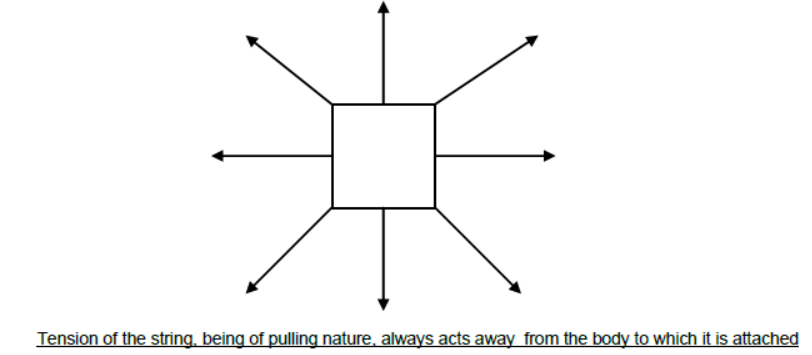
Physical Application
i) Flexible wire holding the lamp pulls the lamp in upward direction and pulls the point of suspension in the downward direction.
ii) Rope holding the bucket in the well pulls the bucket in the upward direction and the pulley in the downward direction.
iii) Rope attached between the cattle and the peg pulls the cattle towards the peg and peg towards the cattle.
iv) When a block is pulled by the chain, the chain pulls the block in forward direction and the person holding the chain in reverse direction.
Key Point
In case of light string, rope, chain, rod etc. tension is same all along their lengths.

Consider a point P on a light (massless) string. Let tensions on either side of it be T1 and T2 respectively and the string be accelerating towards left under these forces. Then for point P
T1 – T2 = ma
Since string is considered to be light mass m of point P is zero
or, T1 – T2 = 0
or, T1 = T2
i) Case – 1
Two bodies connected by a string are placed on a smooth horizontal plane and pulled by a horizontal force.
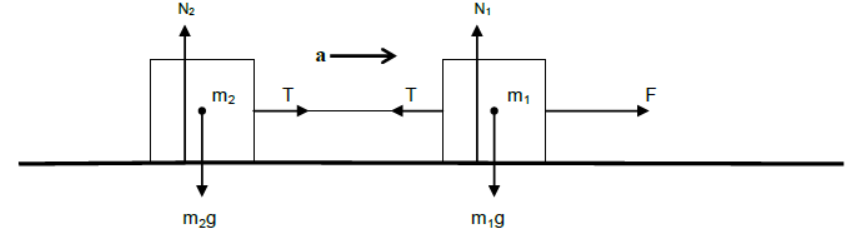
For vertical equilibrium of m1 and m2
N1 = m1g and N2 = m2g
For horizontal acceleration of m1 and m2
F – T = m1a and T = m2a
(Since both the bodies are connected to the same single string they have same acceleration)
ii) Case – 2
Two bodies connected by a horizontal string are placed on a smooth horizontal plane and pulled by a inclined force.
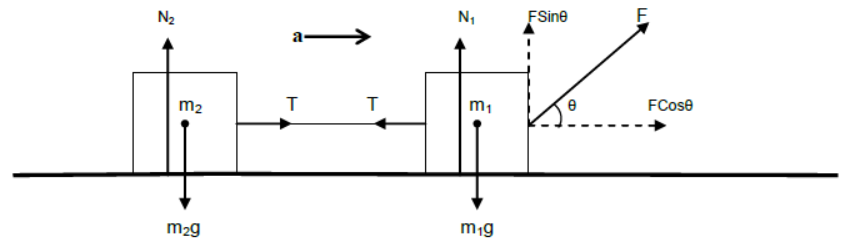
For vertical equilibrium of m1 and m2
N1 + FSinθ = m1g and N2 = m2g
For horizontal acceleration of m1 and m2
FCosθ – T = m1a and T = m2a
(since both the bodies are connected to the same single string they have same accelerations)
iii) Case – 3
Two bodies connected by a inclined string are placed on a smooth horizontal plane and pulled by a inclined force.
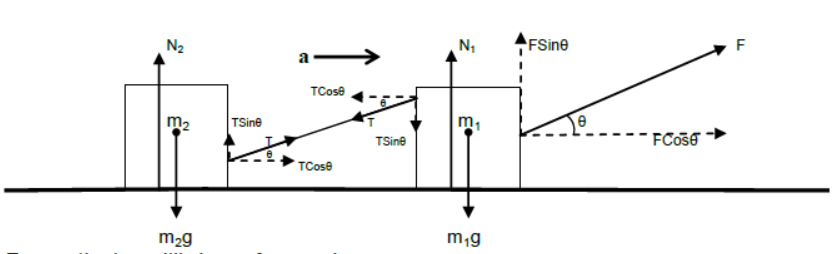
For vertical equilibrium of m1 and m2
N1 + FSinθ = m1g + TSinθ and N2 + TSinθ = m2g
For horizontal acceleration of m1 and m2
FCosθ – TCosθ = m1a and TCosθ = m2a
(since both the bodies are connected to the same single string they have same accelerations)
iv) Case – 4
Two bodies connected by a string made to accelerate up the incline by applying force parallel to the incline.
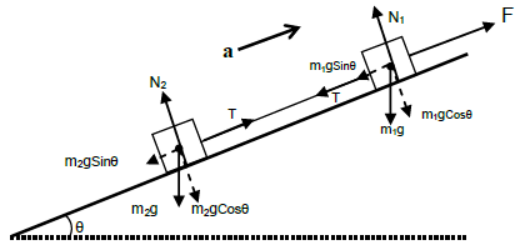
For equilibrium of m1 and m2 in the direction perpendicular to the plane
N1 = m1gCosθ and N2 = m2gCosθ
For acceleration of m1 and m2 up the incline
F – T – m1gSinθ = m1a and T – m2gSinθ = m2a
Tension of A light Rigid Rod
Force applied by rod is also known as its tension. Since rod is rigid, it cannot bend like string. Hence rod can pull as well as push. Tension of rod can be of pulling as well as pushing nature but one at a time. Tension of a rod attached to the body may be directed towards as well as away from the body.

Physical Application
i) Pillars supporting the house pushes the house in the upward direction and pushes the ground in the downward direction.
ii) Wooden bars used in the chair pushes the ground in the downward direction and pushes the seating top in the upward direction.
iii) Parallel bars attached to the ice-cream trolley pushes the trolley in the forward direction and pushes the ice-cream vendor in the backward direction.(when the trolley is being pushed by the vendor)
iv) Rod holding the ceiling fan pulls the fan in the upward direction and pulls the hook attached to the ceiling in the downward direction.
v) Parallel rods attached between the cart and the bull pulls the cart in the forward direction and pulls the bull in the backward direction.
Different Cases of Light Rigid Rod
i) Case – 1
Rod attached from the ceiling and supporting the block attached to its lower end.
Since the block is at rest
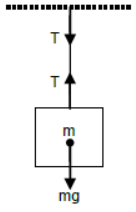
T = mg
ii) Case – 2
Rod is attached between two blocks placed on the horizontal plane and the blocks are accelerated by pushing force.
For vertical equilibrium of m1 and
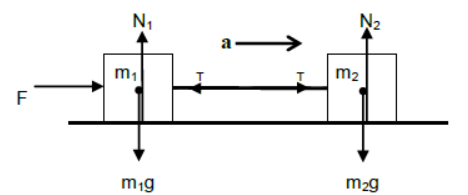
N1 = m1g and N2 = m2g
(Since both the bodies connected to the rod will have same acceleration)
iii) Case – 3
Rod is attached between two blocks placed on the horizontal plane and the blocks are accelerated by pulling force.
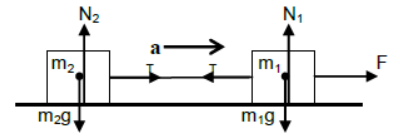
For vertical equilibrium of m1 and m2
N1 = m1g and N2 = m2g
For horizontal acceleration of m1 and m2
F – T = m1a and T = m2a
(Since both the bodies are connected to the same rod they have same acceleration)
iv) Case – 4
Rod is attached between two blocks placed on the incline plane and the blocks are accelerated by pushing parallel to
the incline.
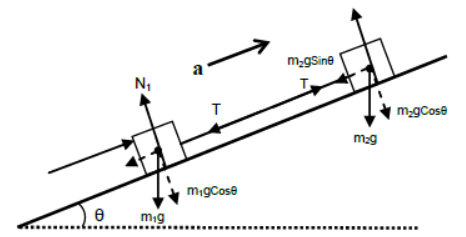
For vertical equilibrium of m1 and m2
N1 = m1gCosθ and N2 = m2gCosθ
For acceleration of m1 and m2 parallel to
the incline m1gCosθ
F – m1gSinθ – T = m1a, θ m1g
T – m2gSinθ = m2a
Fixed Pulley
It is a simple machine in the form of a circular disc or rim supported by spokes having groove at its periphery. It is free to rotate about an axis passing through its center and perpendicular to its plane.
Key Point
In case of light pulley, tension in the rope on both the sides of the pulley is same (to be proved in the rotational mechanics)
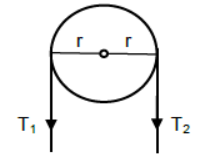
Anticlockwise Torque – Clockwise Torque = Moment of Inertia x Angular acceleration
T1 x r – T2 x r = Iα
Since the pulley is light and hence considered to be massless, it’s moment of inertia
I = 0
or, T1 x r – T2 x r = 0
or, T1 x r = T2 x r
or, T1 = T2
Different Cases of Fixed Pulley
i) Case – 1
Two bodies of different masses (m1 > m2) are attached at two ends of a light string passing over a smooth light pulley
For vertical equilibrium of pulley
T1 = T + T = 2T
For vertical acceleration of m1 and m2
m1g – T = m1a and T – m2g = m2a
m1 accelerates downwards and m2 accelerates upwards(m1>m2)
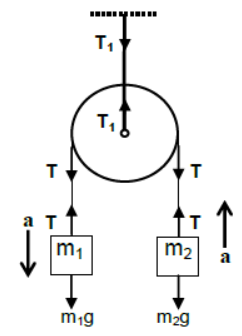
ii) Case – 2
Two bodies of different masses are attached at two ends of a light string passing
over a light pulley. m1 is placed on a horizontal surface and m2 is hanging freely in
air.
For vertical equilibrium m1
N = m1g
For horizontal acceleration of m1
T = m1a
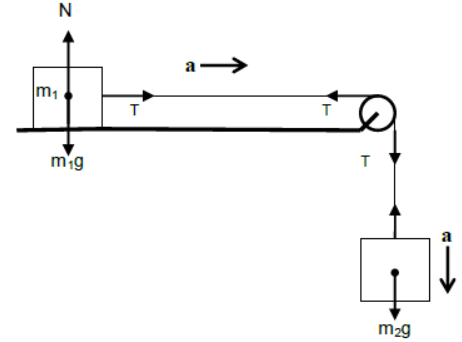
For vertically downward acceleration of m2
m2g – T = m2a
iii) Case – 3
Two bodies of different masses are attached at two ends of a light string passing over a light pulley. m1 is placed on an inclined surface and m2 is hanging freely in air.
For equilibrium of m1 perpendicular to incline plane
N = m1gCosθ
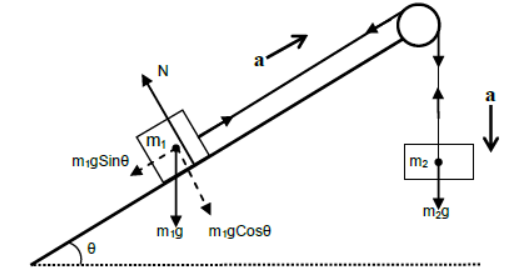
For acceleration of m1 up the incline plane
T – m1gSinθ = m1a
For vertically downward acceleration of m2
m2g – T = m2a
Movable Pulley
The pulley which moves in itself is known as movable pulley.
Key Point
In case of light movable pulley, acceleration of a body (pulley) goes on decreasing on increasing the number of strings attached to it. That is the body attached with two ropes moves with half the acceleration of the body attached with single rope.
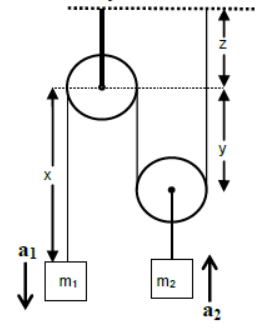
Length of the string is constant
x + 2y + z = L (Constant)
Differentiating both sides with respect to t (Time)
dx + 2dy + dz = dL
dt dt dt dt y
or, v1 + 2v2 + 0 = 0 (z and L are constant)
or, v1 + 2v2 = 0
Again differentiating both sides with respect to
dv1 + 2dv2 = 0
dt dt
or, a1 + 2a2 = 0
or, a1 = – 2a2
That is acceleration of m1 (body attached to a single string) is opposite and twice the acceleration of m2 (body attached to a double string)
Different Cases of Light Movable Pulley
i) Case – 1
Mass m1 is attached at one end of the string and the other end is fixed to a rigid support. Mass m2 is attached to the light movable pulley.
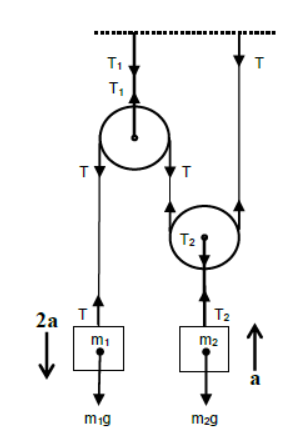
For vertical acceleration of m1
m1g – T = m12a (m1 is connected to a single string)
For vertical acceleration of m2
T2 – m2g = m2a
(m1 accelerates downwards and m2 accelerates upwards since m1>2m2)
For the clamp holding the first pulley
T1 = 2T
For the clamp holding the movable pulley
2T – T2 = mpulleya
or, 2T – T2 = 0 (light pulley)
or, 2T = T2
ii) Case – 2
Mass m1 is attached at one end of the string and placed on a smooth horizontal surface and the other end is fixed to a rigid support after passing through a light movable suspended pulley. Mass m2 is attached to the light movable pulley.
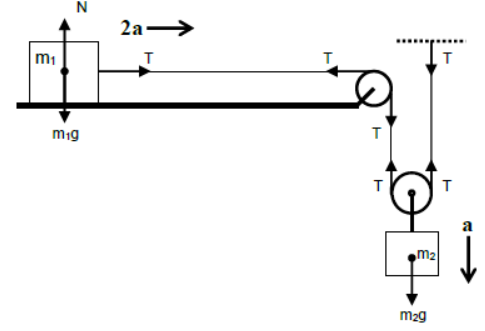
For vertical equilibrium of m1
N = m1g
For horizontal acceleration of m1
T = m12a
For vertical motion of m2
m2g – 2T = m2a
iii) Case – 3
Mass m1 is attached to the movable pulley and placed on a smooth horizontal surface. One end of the string is attached to the clamp holding the pulley fixed to the horizontal surface and from its other end mass m2 suspended.
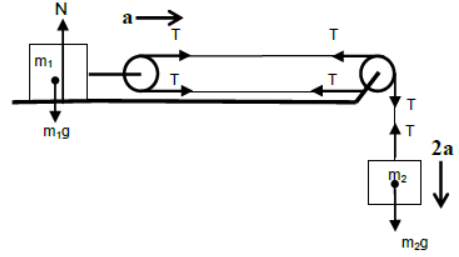
For vertical equilibrium of m1
N = m1g
For horizontal motion of m1
2T = m1a
For vertical motion of m2
m2g – T = m22a
iv) Case – 4
Mass m1 is attached to a movable pulley and placed on a smooth inclined surface.
Mass m2 is is suspended freely from a fixed light pulley.
For equilibrium of m1 perpendicular to incline plane
N = m1gCosθ
For acceleration of m1 up the incline plane
2T – m1gSinθ = m1a
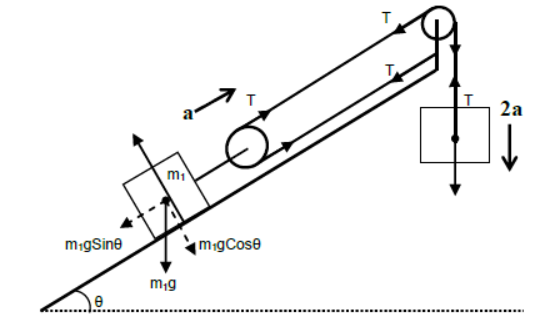
For vertically downward acceleration of m2
m2g – T = m22a
Newton’ 3rd law or Law of Action and Reaction
Every action is opposed by an equal and opposite reaction.
or
For every action there is an equal and opposite reaction.

F12 is the force on the first body (m1) due to second body (m2)
F21 is the force on the second body (m2) due to first body (m1)

Numerical Application
Force on the first body due to second body (F12) is equal and opposite to
the force on the second body due to first body (F21).
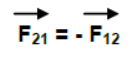
Physical Application
i) When we push any block in the forward direction then block pushes us in the backward direction with an equal and opposite force.
ii) Horse pulls the rod attached to the cart in the forward direction and the tension of the rod pulls the cart in the backward direction.
iii) Earth pulls the body on its surface in vertically downward direction and the body
pulls the earth with the same force in vertically upward direction.
iv) While walking we push the ground in the backward direction using static frictional force and the ground pushes us in the forward direction using static frictional force.
v) When a person sitting on the horse whips the horse and horse suddenly accelerates, the saddle on the back of the horse pushes the person in the forward direction using static frictional force and the person pushes the saddle in the backward direction using static frictional force.
Note – Normal reaction of the horizontal surface on the body is not the reaction of the weight of the body because weight of the body is the force with which earth attracts the body towards its center, hence its reaction must be the force with which body attracts earth towards it.
Linear Momentum
It is defined as the quantity of motion contained in the body.
Mathematically it is given by the product of mass and velocity. It is a vector quantity represented by p.
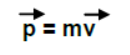
Principle Of Conservation Of Linear Momentum
It states that in the absence of any external applied force total momentum of a system remains conserved.
Proof-
We know that,

Physical Application
i) Recoil of gun – when bullet is fired in the forward direction gun recoils in the backward direction.
ii) When a person jumps on the boat from the shore of river, boat along with the person on it moves in the forward direction.
iii) When a person on the boat jumps forward on the shore of river, boat starts moving in the backward direction.
iv) In rocket propulsion fuel is ejected out in the downward direction due to which rocket is propelled up in vertically upward direction.
Different Cases of Conservation of Linear Momentum

Recoil of gun
Let mass of gun be mg and that of bullet be mb.
Initially both are at rest, hence their initial momentum is zero.
pi = mgug + mbub = 0
Finally when bullet rushes out with velocity vg, gun recoils with velocity vb, hence
their final momentum is
pf = mgvg + mbvb
Since there is no external applied force, from the principal of conservation of linear momentum
pf = pf
or, mgvg + mbvb = 0
or, mgvg = -mbvb
or, vg = – mbvb/ mg
From above expression it must be clear that
1. Gun recoils opposite to the direction of motion of bullet.
2. Greater is the mass of mullet mb or velocity of bullet vb greater is the recoil of the gun.
3. Greater is the mass of gun mg, smaller is the recoil of gun.
Impulse and Impulsive Force
Impulsive Force
The force which acts on a body for very short duration of time but is
still capable of changing the position, velocity and direction of motion of the body up
to large extent is known as impulsive force.
Example –
1. Force applied by foot on hitting a football.
2. Force applied by boxer on a punching bag.
3. Force applied by bat on a ball in hitting it to the boundary.
4. Force applied by a moving truck on a drum.
Note- Although impulsive force acts on a body for a very short duration of time yet its magnitude varies rapidly during that small duration.
Impulse
Impulse received by the body during an impact is defined as the product of average impulsive force and the short time duration for which it acts.
I = Favg x t
Relation Between Impulse and Linear Momentum
Consider a body being acted upon by an impulsive force, this force
changes its magnitude rapidly with the time. At any instant if impulsive force is F
then elementary impulse imparted to the body in the elementary time dt is given by
dI = F x dt
Hence total impulse imparted to the body from time t1 to t2 is
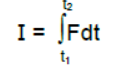
But from Newton’s second law we know that
F = dp
dt
or, Fdt = dp
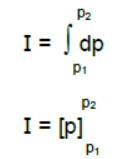
or, I = p2 – p1
Hence impulse imparted to the body is equal to the change in its momentum.
Graph Between Impulsive Force and Time
With the time on x axis and impulsive force on y axis the graph of the following nature is obtained
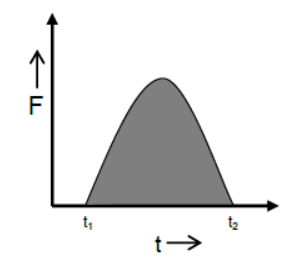
Area enclosed under the impulsive force and time graph from t1 to t2 gives the impulse imparted to the body from time t1 to t2.
Physical Application
i) While catching a ball a player lowers his hand to save himself from getting hurt.
ii) Vehicles are provided with the shock absorbers to avoid jerks.
iii) Buffers are provided between the bogies of the train to avoid jerks.
iv) A person falling on a cemented floor receive more jerk as compared to that falling on a sandy floor.
v) Glass wares are wrapped in a straw or paper before packing.
Equilibrium of Concurrent Forces
If the number of forces act at the same point, they are called concurrent forces. The condition or the given body to be in equilibrium under the number of forces acting on the body is that these forces should produce zero resultant.
The resultant of the concurrent forces acting on a body will be zero if they can be represented completely by the sides of a closed polygon taken in order.
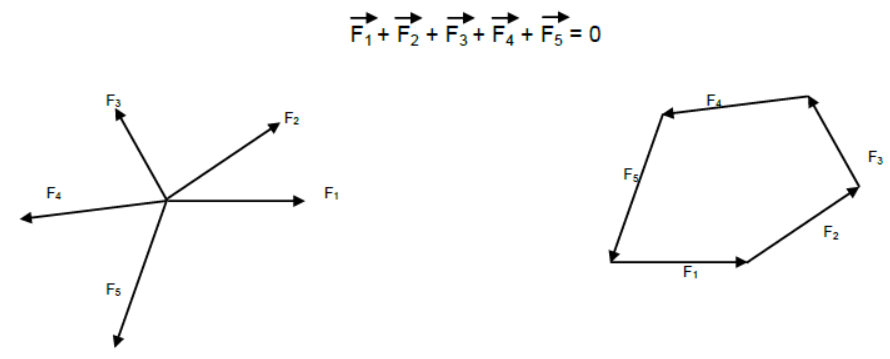
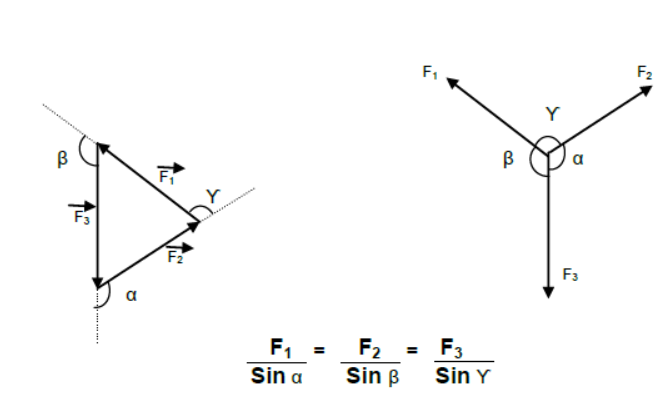
Lami’s Theorem – It states that the three forces acting at a point are in equilibrium if each force is proportional the sine of the angle between the other two forces.
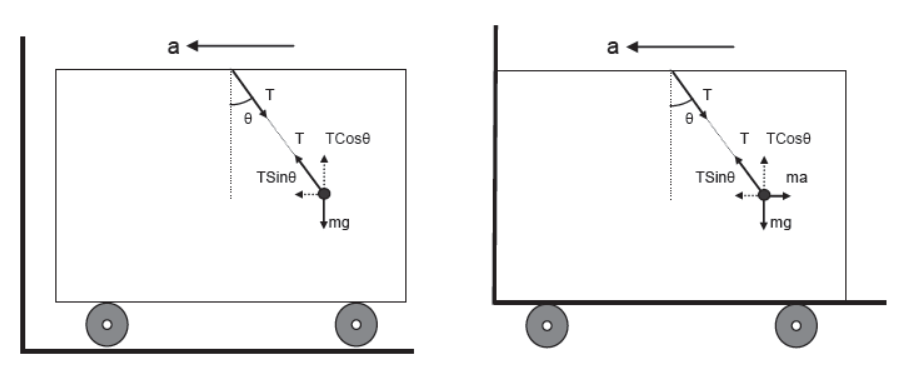
Inertial and Non-inertial Frame of Reference
Frame of reference is any frame with respect to which the body is analyzed. All the frames which are at rest or moving with a constant velocity are said to be inertial frame of reference. In such frame of reference all the three laws of Newton are applicable.
Any accelerated frame of reference is said to be non-inertial frame of reference. In such frames all the three laws of Newton are not applicable as such. In order to apply Newton’s laws of motion in a non-inertial frame, along with all other forces a pseudo force F = ma must also be applied on the body opposite to the direction of acceleration of the frame.

Reading of Spring Balance
Reading of a spring balance is equal to the tension in the spring of the balance but measured in kilogram.
Reading = T kgf/ g
Reading of Weighing Machine
Reading of a weighing machine is equal to the normal reaction
applied by the machine but measured in kilogram.
Reading = N kgf/ g
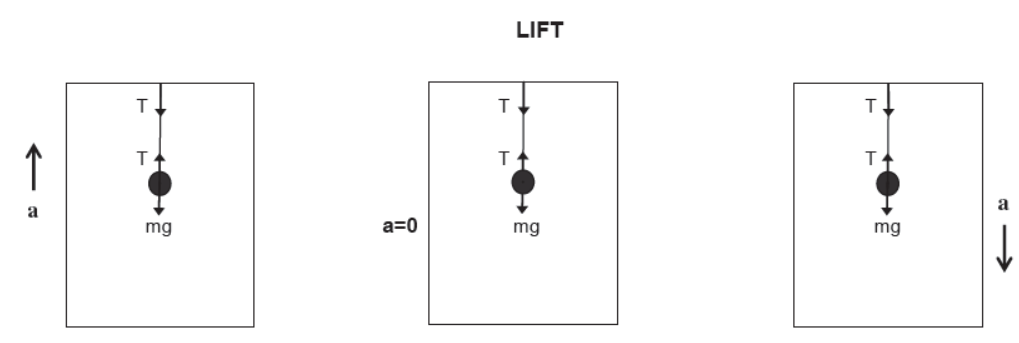
Observer Outside the Lift

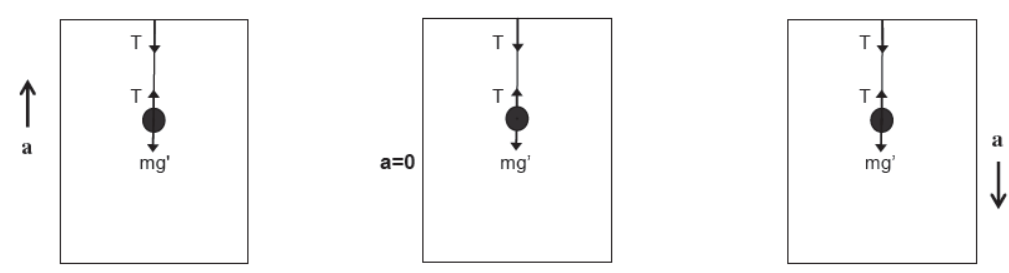
Observer Inside the Lift
(Body is at rest according to the observer inside the lift)

MEMORY MAP
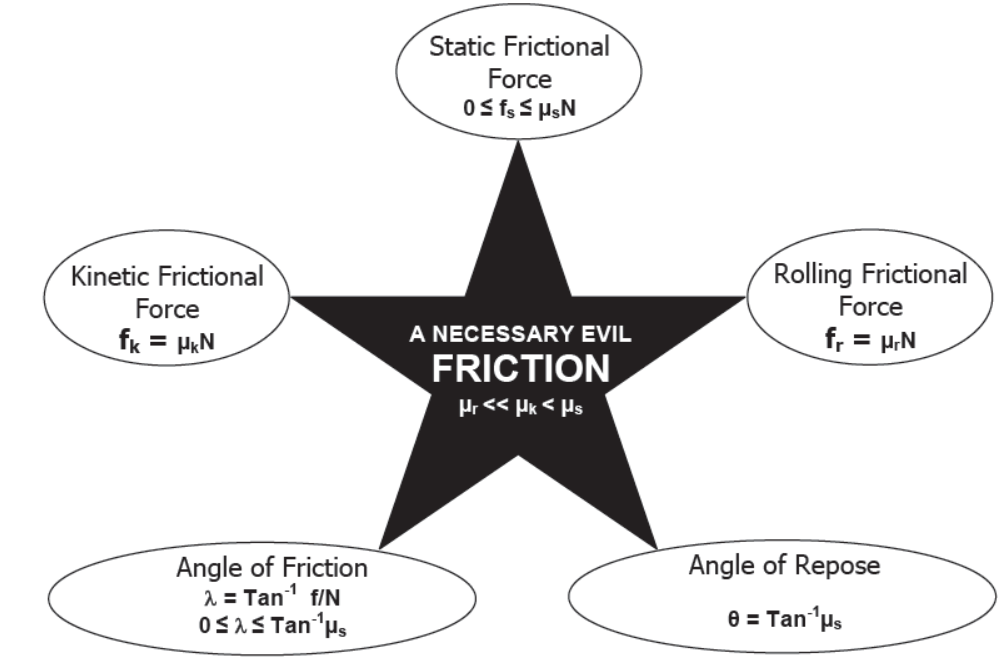
FRICTION
Friction – The property by virtue of which the relative motion between two surfaces in contact is opposed is known as friction.
Frictional Forces – Tangential forces developed between the two surfaces in contact, so as to oppose their relative motion are known as frictional forces or commonly friction.
Types of Frictional Forces – Frictional forces are of three types :-
1. Static frictional force
2. Kinetic frictional force
3. Rolling frictional force
Static Frictional Force – Frictional force acting between the two surfaces in contact which are relatively at rest, so as to oppose their relative motion, when they tend to move relatively under the effect of any external force is known as static frictional force. Static frictional force is a self adjusting force and its value lies between its minimum value up to its maximum value.
Minimum value of static frictional force – Minimum value of static frictional force is zero in the condition when the bodies are relatively at rest and no external force is acting to move them relatively.
fs(min) = 0
Maximum value of static frictional force – Maximum value of static frictional force is μsN (where μs is the coefficient of static friction for the given pair of surface and N is the normal reaction acting between the two surfaces in contact) in the condition when the bodies are just about to move relatively under the effect of external applied force.
fs(max) = μsN
Therefore, fs(min) ≤ fs ≤ fs(max)
or, 0 ≤ fs ≤ μsN
Kinetic Frictional Force – Frictional force acting between the two surfaces in contact which are moving relatively, so as to oppose their relative motion, is known as kinetic frictional force. It’s magnitude is almost constant and is equal to μkN where μk is the coefficient of kinetic friction for the given pair of surface and N is the normal reaction acting between the two surfaces in contact. It is always less than maximum value of static frictional force.
fk = μkN
Since, fk < fs(max) = μsN
Therefore, μkN < μsN
or, μk < μs
Limiting Frictional Force – The maximum value of static frictional force is the maximum frictional force which can act between the two surfaces in contact and hence it is also known as limiting frictional force.
Laws of Limiting Frictional Force –
1. Static friction depends upon the nature of the surfaces in contact.
2. It comes into action only when any external force is applied to move the two bodies relatively, with their surfaces in contact.
3. Static friction opposes the impending motion.
4. It is a self adjusting force.
5. The limiting frictional force is independent of the area of contact between the two surfaces.
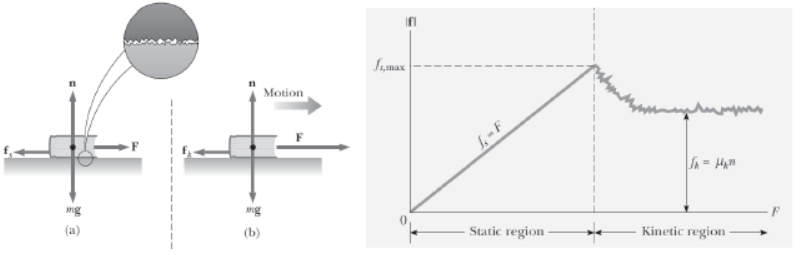
Modern View – According to modern theory the cause of friction is the atomic and molecular forces of attraction between the two surfaces at their actual point of contact. When any body comes in contact with any other body then due to their roughness at the microscopic level they come in actual contact at several points. At these points the atoms and molecules come very close to each other and intermolecular force of attraction start acting between them which opposes their relative motion.
Contact Force – The forces acting between the two bodies due to the mutual contact of their surfaces are known as contact forces. The resultant of all the contact forces acting between the bodies is known as resultant contact force. Example
friction (f) and normal reaction (N) are contact forces and their resultant (Fc) is the resultant is the resultant contact force.
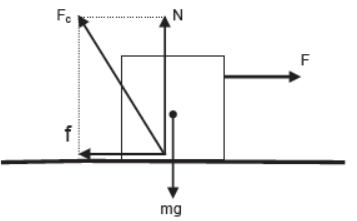
Fc = √ f2 + N2
Since maximum value of frictional force is Limiting frictional force (μsN) Therefore maximum value of contact force is
Fc(max) = √ (μsN) 2 + N2
or, Fc(max) = N√ μs
2 + 12
or, Fc(max) = N√ μs
2 + 1
Angle of Friction – The angle between the resultant contact force (of normal reaction and friction) and the normal reaction is known as the angle of friction.
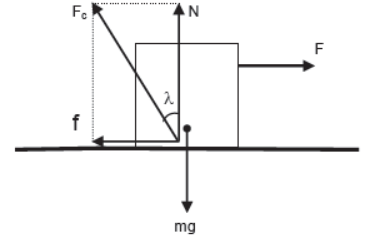
Tan λ = f / N
or, λ = Tan-1 f/ N
or, λ max = Tan-1 f max/N
or, λ max = Tan-1 μsN/N
or, λ max = Tan-1 μs
Angle of Repose – The angle of the inclined plane at which a body placed on it just begins to slide is known as angle of repose.
Perpendicular to the plane
N = mgCosθ (since body is at rest)
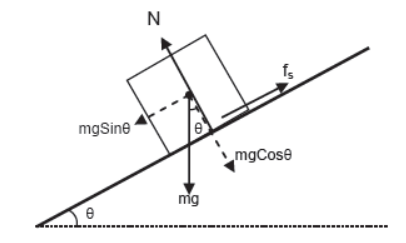
Parallel to the plane when body is at rest
mgSinθ = fs
When body is just about to slide
mgSinθ = fs(max) = μsN = μsmgCosθ
or, Tanθ = μs
or, θ = Tan-1/μs
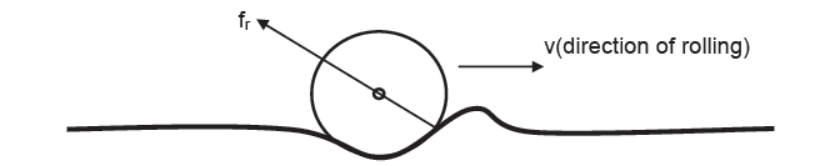
Note – Angle of repose is equal to the maximum value of angle of friction Rolling Frictional Force – Frictional force which opposes the rolling of bodies (like cylinder, sphere, ring etc.) over any surface is called rolling frictional force. Rolling frictional force acting between any rolling body and the surface is almost constant and is given by μrN. Where μr is coefficient of rolling friction and N is the normal reaction between the rolling body and the surface.
fr = μrN
Note – Rolling frictional force is much smaller than maximum value of static and kinetic frictional force.
fr << fk < fs(max)
or, μrN << μkN < μsN
or, μr << μk < μs
Cause of Rolling Friction – When any body rolls over any surface it causes a little depression and a small hump is created just ahead of it. The hump offers resistance to the motion of the rolling body, this resistance is rolling frictional force. Due to this reason only, hard surfaces like cemented floor offers less resistance as compared to soft sandy floor because hump created on a hard floor is much smaller as compared to the soft floor.
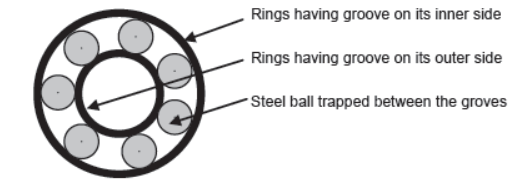
Need to Convert Kinetic Friction into Rolling Friction – Of all the frictional forces rolling frictional force is minimum. Hence in order to avoid the wear and tear of machinery it is required to convert kinetic frictional force into rolling frictional force and for this reason we make the use of ball-bearings.
Friction: A Necessary Evil – Although frictional force is a non-conservative force and causes lots of wastage of energy in the form of heat yet it is very useful to us in many ways. That is why it is considered as a necessary evil.
Advantages of Friction –
i) Friction is necessary in walking. Without friction it would have been impossible for us to walk.
ii) Friction is necessary for the movement of vehicles on the road. It is the static frictional force which makes the acceleration and retardation of vehicles possible on the road.
iii) Friction is helpful in tying knots in the ropes and strings.
iv) We are able to hold anything with our hands by the help of friction only.
Disadvantages of Friction –
i) Friction causes wear and tear in the machinery parts.
ii) Kinetic friction wastes energy in the form of heat, light and sound.
iii) A part of fuel energy is consumed in overcoming the friction operating within the various parts of machinery.
Methods to Reduce Friction –
i) By polishing – Polishing makes the surface smooth by filling the space between the depressions and projections present in the surface of the bodies at microscopic level and there by reduces friction.
ii) By proper selection of material – Since friction depends upon the nature of material used hence it can be largely reduced by proper selection of materials.
iii) By lubricating – When oil or grease is placed between the two surfaces in contact, it prevents the surface from coming in actual contact with each other. This converts solid friction into liquid friction which is very small.
Physical Application
Horizontal Plane
i) Body kept on horizontal plane is at rest and no force is applied.
For vertical equilibrium
N = mg
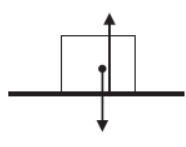
ffriction = 0 (friction is a opposing force and there is no external applied force)
ii) Body kept on horizontal plane is at rest under single horizontal force.
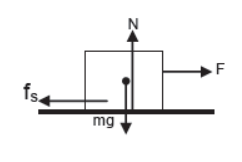
For vertical equilibrium
N = mg (since body is at rest)
For horizontal equilibrium (since body is at rest)
F = fs
iii) Body kept on horizontal plane is just about to move.
For vertical direction
N = mg (since body is at rest)
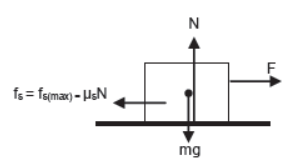
For horizontal direction (since body is just about to move)
F = fs = fs(max) = μsN
iv) Body kept on horizontal plane is accelerating horizontally.
For vertical direction
N = mg (since body is at rest)
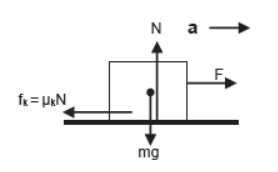
For horizontal direction
F – fk = ma
or, F – μkN = ma
v) Body kept on horizontal plane is accelerating horizontally towards right under single upward inclined force.
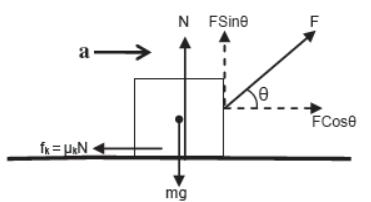
For vertical direction
N + FSinθ = mg (since body is at rest)
For horizontal direction
FCosθ – fk = ma
or, FCosθ – μkN = ma
vi) Body kept on horizontal plane is accelerating horizontally towards right under single downward inclined force.
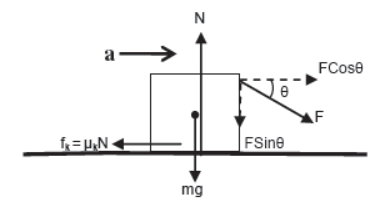
For vertical direction
N = FSinθ + mg (since body is at rest)
For horizontal direction
FCosθ – fk = ma
or, FCosθ – μkN = ma
vii) Body kept on horizontal plane is accelerating horizontally towards right under an inclined force and an opposing horizontally applied force.
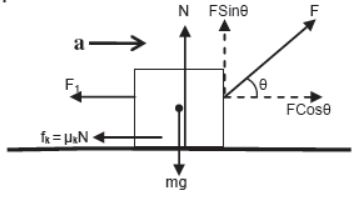
For vertical direction
N + FSinθ = mg (since body is at rest)
For horizontal direction
FCosθ – F1 – fk = ma
or, FCosθ – F1 – μkN = ma
vi) Body kept on horizontal plane is accelerating horizontally towards right under two inclined forces acting on opposite sides.
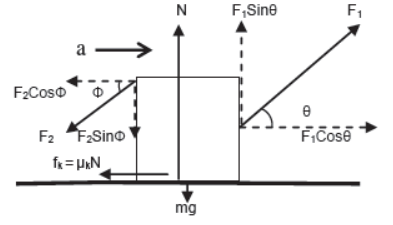
For vertical direction(since body is at rest)
N + F1Sinθ = mg + F2 SinФ
For horizontal direction
F1Cosθ – F2CosФ – μkN = ma
Inclined Plane
i) Case – 1
Body is at rest on inclined plane.
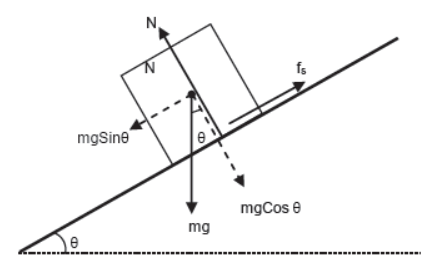
Perpendicular to the plane
N = mgCosθ (since body is at rest)
Parallel to the plane (since body is at rest)
mgSinθ = fs
ii) Case – 2
Body is just about to move on inclined plane.
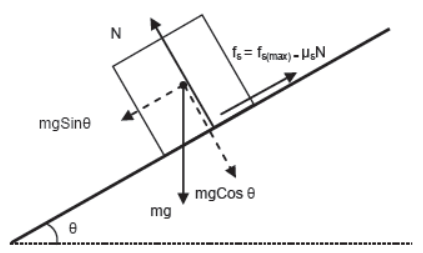
Perpendicular to the plane
N = mgCosθ (since body is at rest)
Parallel to the plane (since body is at rest)
mgSinθ = fs = fs(max) = μsN
iii) Case – 3
Body is accelerating downwards on inclined plane.
Perpendicular to the plane
N = mgCosθ (since body is at rest)
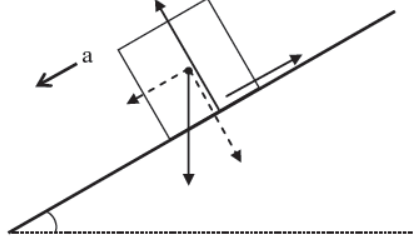
Parallel to the plane
mgSinθ – fk = ma
or, mgSinθ – μkN = ma
iv) Case – 4
Body is accelerating up the incline under the effect of force acting parallel to the incline.
Perpendicular to the plane
N = mgCosθ (since body is at rest)
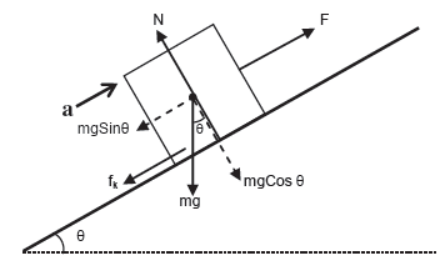
Parallel to the plane
F – fk – mgSinθ = ma
or, F – μkN – mgSinθ = ma
v) Case – 5
Body accelerating up the incline under the effect of horizontal force.
Perpendicular to the plane
N = mgCosθ + FSinθ (since body is at rest)
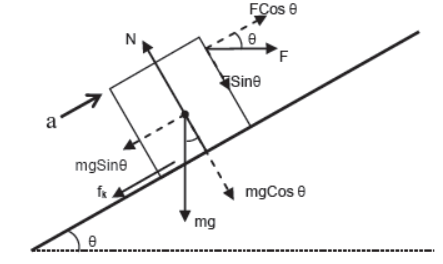
Parallel to the plane
FCosθ – mgSinθ – fk = ma
or, FCosθ – mgSinθ – μkN ma
Vertical Plane
i) Case – 1
Body pushed against the vertical plane by horizontal force and is at rest.
For horizontal direction (since body is at rest)
F = N
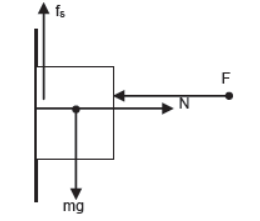
For vertical direction
mg = fs
ii) Case – 2
Body pushed against the vertical plane by horizontal force and pulled vertically
upward
For horizontal direction (since body is at rest)
F = N
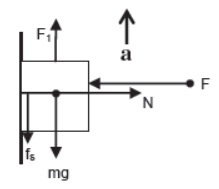
For vertical direction
F1 – mg – fs = ma
iii) Case – 3
Body pushed against the vertical plane by inclined force and accelerates vertically upward.
For horizontal direction
N = FSinθ (since body is at rest)
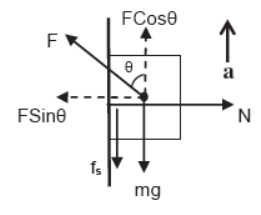
For vertical direction
FCosθ – mg – fs = ma
MEMORY MAP
Circular Motion – When a body moves such that it always remains at a fixed distance from a fixed point then its motion is said to be circular motion. The fixed distance is called the radius of the circular path and the fixed point is called the center of the circular path.
Uniform Circular Motion – Circular motion performed with a constant speed is known as uniform circular motion.
Angular Displacement – Angle swept by the radius vector of a particle moving on a circular path is known as angular displacement of the particle. Example :– angular displacement of the particle from P1 to P2 is θ.
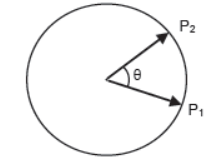
Relation Between Angular Displacement and Linear Displacement –
Since, Angle = arc
radius
Anglular Displacement = arc P1P2 / radius
θ = s/ r
Angular Velocity – Rate of change of angular displacement of a body with respect to time is known as angular displacement. It is represented by ω.
Average Angular Velocity – It is defined as the ratio of total angular displacement to total time taken.
ωavg = Total Angular Displacement/Total Time Taken
ωavg = Δθ/Δ t
Instantaneous Angular Velocity – Angular velocity of a body at some particular instant of time is known as instantaneous angular velocity.
Or
Average angular velocity evaluated for very short duration of time is
known as instantaneous angular velocity.
ω = Lim ωavg = Δθ
Δ t→0 Δt
ω = dθ/dt
Relation Between Angular Velocity and Linear Velocity
We know that angular velocity
ω = dθ/dt
Putting, θ = s/r
ω = d (s/r)/dt
or, ω = 1 ds/r dt
or, ω = v/r
or, v = rω
Time Period of Uniform Circular Motion – Total time taken by the particle performing uniform circular motion to complete one full circular path is known as
time period.
In one time period total angle rotated by the particle is 2π and time period is T.
Hence angular velocity
ω = 2π /T
or, T = 2π/ω
Frequency – Number of revolutions made by the particle moving on circular path in one second is known as frequency.
f = 1/T = ω/ 2π
Centripetal Acceleration – When a body performs uniform circular motion its speed remains constant but velocity continuously changes due to change of direction.
Hence a body is continuously accelerated and the acceleration experienced by the body is known as centripetal acceleration (that is the acceleration directed towards the center).
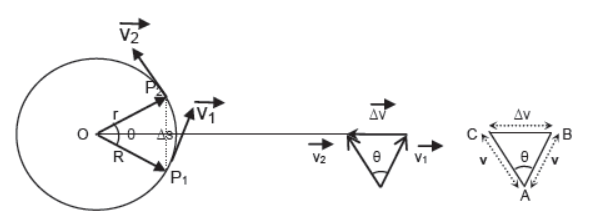
Consider a particle performing uniform circular motion with speed v.
When the particle changes its position from P1 to P2 its velocity changes from →v1 to →v2 due to change of direction. The change in velocity from P1 to P2 is →Δv which is directed towards the center of the circular path according to triangle law of subtraction of vectors. From figure ΔOP1P2 and ΔABC are similar, hence applying the condition of similarity
BC/AB = P1/O P1/P1
or, Δv/v = Δs/r
or, Δv = vΔs/r
Dividing both sides by Δv/Δt , = vΔs/rΔt
Taking limit Δt → 0 both sides,
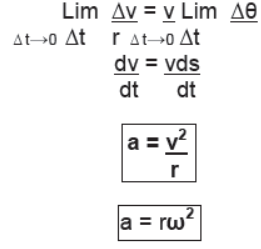
Since the change of velocity is directed towards the center of the circular path, the acceleration responsible for the change in velocity is also directed towards center of circular path and hence it is known as centripetal acceleration.
Centripetal Force – Force responsible for producing centripetal acceleration is known as centripetal force. Since centripetal acceleration is directed towards the center of the circular path the centripetal force is also directed towards the center of the circular path.

If a body is performing uniform circular motion with speed v and angular velocity ω on a circular path of radius r, then centripetal acceleration is given by Net Acceleration of a Body Performing Non-Uniform Circular Motion When a body performs non-uniform circular motion its speed i.e. magnitude of instantaneous velocity varies with time due to which it experiences tangential acceleration aT along with the centripetal acceleration aC. Since both the accelerations act simultaneously on a body and are mutually perpendicular to each other, the resultant acceleration aR is given by their vector sum.
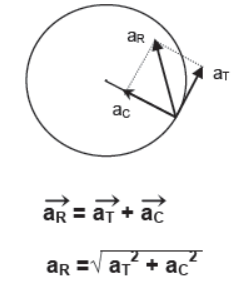
Physical Application of Centripetal Force
i) Case – 1
Circular motion of a stone tied to a string.
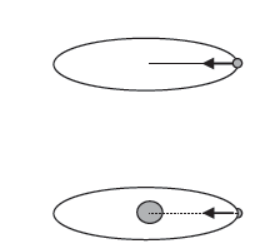
Centripetal force is provided by the tension of the string
Fc = mv2/r = T
ii) Case – 2
Circular motion of electron around the nucleus.
Centripetal force is provided by the electrostatic force of attraction between the
positively charged nucleus and negatively charged electron
Fc = mv2/r = FE
iii) Case – 3
Circular motion of planets around sun or satellites around planet.
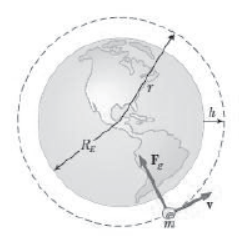
Centripetal force is provided by the gravitational force of attraction between the planet and sun
Fc = mv2/r = Fg
iv) Case – 4
Circular motion of vehicles on a horizontal road.
Centripetal force is provided by the static frictional force between the road and the tyre of the vehicle.
Fc = mv2/r = fs
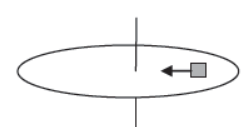
v) Case – 5
Circular motion of a block on rotating platform.
Centripetal force is provided by the static frictional force between the block and the platform.
Fc = mv2/r = fs
vi) Case – 6
Circular motion of mud particles sticking to the wheels of the vehicle.
Centripetal force is provided by the adhesive force of attraction between the mud particles and the tyres of the vehicle.
Fc = mv2/r = Fadhesive
At very high speed when adhesive force is unable to provide necessary centripetal force, the mud particles fly off tangentially. In order to prevent the particles from staining our clothes, mud-guards are provided over the wheels of vehicle.

vii) Case – 7
Circular motion of a train on a horizontal track.
Centripetal force is provided by the horizontal component of the reaction force applied by the outer track on the inner projection of the outer wheels
Fc = mv2/r = NHorizontal
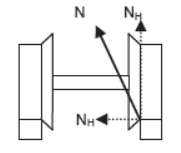
viii) Case – 8
Circular motion of a toy hanging from ceiling of vehicle.
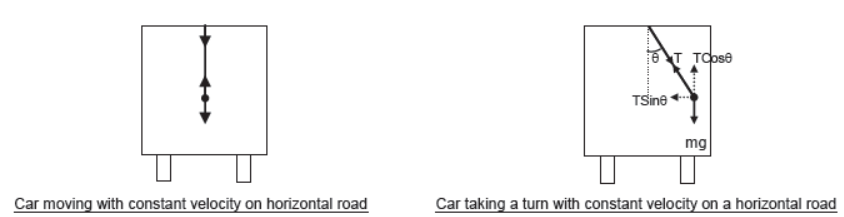
Whenever car takes a turn, string holding the toy gets tilted outward such that the vertical component of the tension of string balances the weight of the body and the horizontal component of tension provides the necessary centripetal force.
TSinθ = mv2/r
TCosθ = mg
Therefore, Tanθ = v2/rg
ix) Case – 9
Conical pendulum.
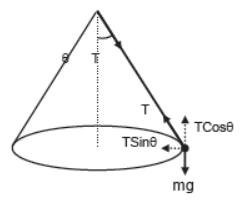
Whenever bob of a pendulum moves on a horizontal circle it’s string generates a cone. Such a pendulum is known as conical pendulum. The vertical component of the tension of the string balances the weight of the body and the horizontal component of tension provides the necessary centripetal force.
TSinθ = mv2/r
TCosθ = mg
Therefore, Tanθ = v2/rg
x) Case – 10
Well of death.
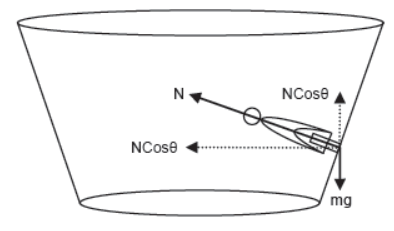
In the well of death, the rider tries to push the wall due to its tangential velocity in the outward direction due to which wall applies normal reaction in the inward direction.
The vertical component of the normal reaction balances the weight of the body and its horizontal component provides the necessary centripetal force.
NSinθ = mv2/r
NCosθ = mg
Therefore, Tanθ = v2/rg
xi) Case – 11
Turning of aero plane.
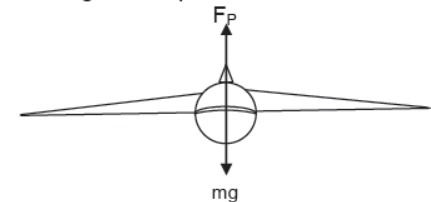
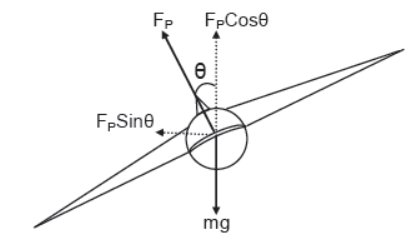
While taking a turn aero-plane tilts slightly inwards due to which it’s pressure force also gets tilted inwards due to which it’s pressure force also gets tilted inwards such that it’s vertical component balances the weight of the body and the horizontal component provides the necessary centripetal force.
FPSinθ = mv2/r
FPCosθ = mg
Therefore, Tanθ = v2/rg
xi) Case – 11
Banking of Roads
In case of horizontal road necessary centripetal force mv2/r is provided by static frictional force. When heavy vehicles move with high speed on a sharp turn (small radius) then all the factors contribute to huge centripetal force which if provided by the static frictional force may result in the fatal accident.
To prevent this roads are banked by lifting their outer edge. Due to this, normal reaction of road on the vehicle gets tilted inwards such that it’s vertical component balances the weight of the body and the horizontal component provides the necessary centripetal force.
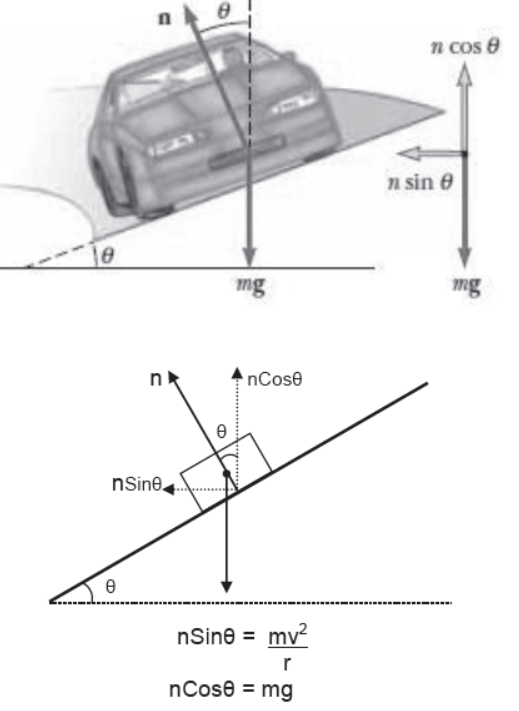
nSinθ = mv2/r
nCosθ = mg
Therefore, Tanθ = v2/rg
xii) Case – 12
Bending of Cyclist
In case of a cyclist moving on a horizontal circular track necessary centripetal force is provided by static frictional force acting parallel along the base. As this frictional force is not passing from the center of mass of the system it tends to rotate the cycle along with the cyclist and make it fall outward of the center of the circular path.
To prevent himself from falling, the cyclist leans the cycle inwards towards the center of the circle due to which the normal reaction of the surface of road on the cycle also leans inward such that that its vertical component balances the weight of the body and the horizontal component provides the necessary centripetal force.
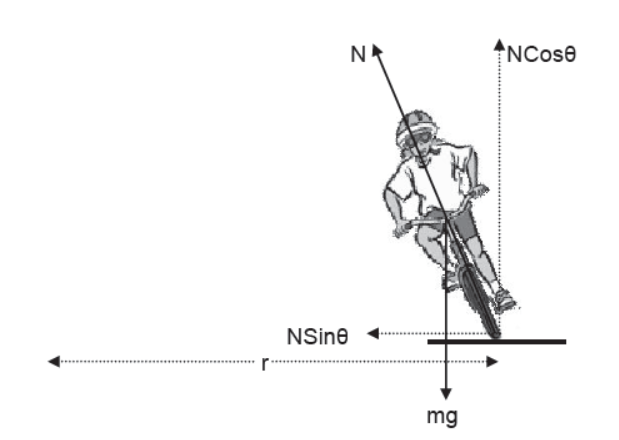
NSinθ = mv2/r
NCosθ = mg
Therefore, Tanθ = v2/rg
xiii) Case – 13
Motion of a Ball in a Bowl
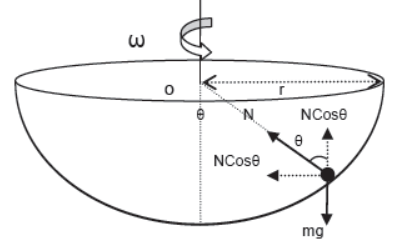
When the bowl rotates with some angular velocity ω. The vertical component of the normal reaction of the bowl on the ball balances the weight of the body and its horizontal component provides the necessary centripetal force.
NSinθ = mv2/r
NCosθ = mg
Therefore, Tanθ = v2/rg
xiv) Case – 14
Motion of a train on the banked tracks.
At the turns tracks are banked by slightly elevating the outer tracks with respect to the inner ones. This slightly tilts the train inwards towards the center of the circular path due to which the normal reaction of the tracks on the train also gets slightly tilted inwards such that the vertical component of the normal reaction balances the weight of the train and it’s horizontal component provides the necessary centripetal force.
NSinθ = mv2/r
NCosθ = mg
Therefore, Tanθ = v2/rg
Vertical Circular Motion
Whenever the plane of circular path of body is vertical its motion is said to be vertical circular motion.
Vertical Circular Motion of a Body Tied to a String
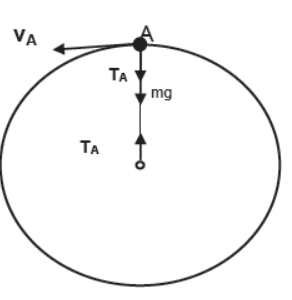
Consider a body of mass m tied to a string and performing vertical circular motion on a circular path of radius r. At the topmost point A of the body weight of the body mg and tension TA both are acting in the vertically downward direction towards the center of the circular path and they together provide centripetal force.
TA + mg = mvA2/r
Critical velocity at the top most point
As we go on decreasing the vA , tension TA also goes on decreasing and in the critical condition when vA is minimum tension TA = 0. The minimum value of vA in this case is known as critical velocity TA(Critical) at the point A. From above
0 + mg = mvA(Critical)2/r
or, vA(Critical)2 = rg
or, vA(Critical)= √rg
If the velocity at point A is less than this critical velocity then the string will slag and the body in spite of moving on a circular path will tend to fall under gravity.
Critical velocity at the lower most point
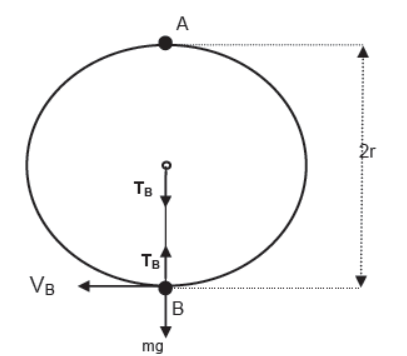
Taking B as reference level of gravitational potential energy and applying energy conservation
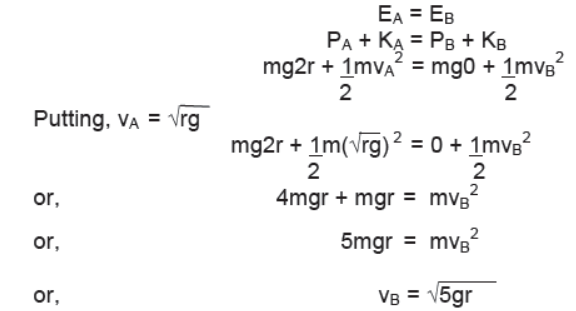
This is the minimum possible velocity at the lower most point for vertical circular motion known as critical velocity at point B.
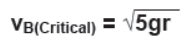
Tension at lowermost point in critical condition
For lowermost point B net force towards the center is centripetal force. Tension TB acts towards the center of the circular path whereas weight mg acts away from it. Hence,
TB – mg = m5gr/r
or, TB = 6mg
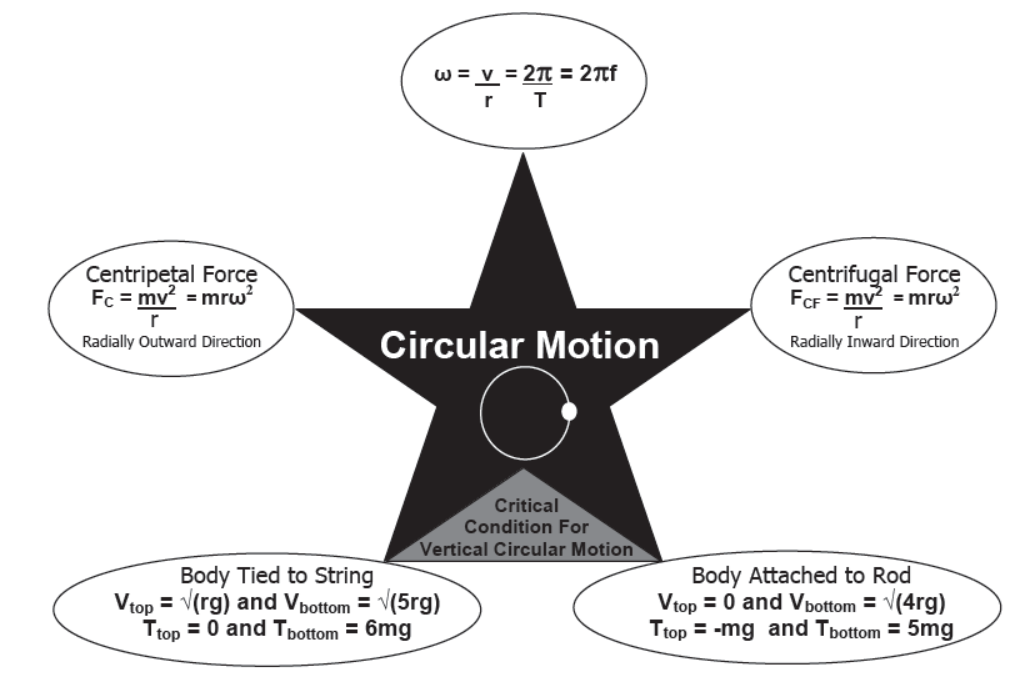
Hence in critical condition of vertical circular motion of a body tied to a string velocities at topmost and lowermost be √(rg) and √(5rg) respectively and tensions in the strings be 0 and 6mg respectively.
General Condition for Slagging of String in Vertical Circular Motion
For the body performing vertical circular motion tied to a string, slagging of string occurs in the upper half of the vertical circle. If at any instant string makes angle θ with vertical then applying net force towards center is equal to centripetal force, we have
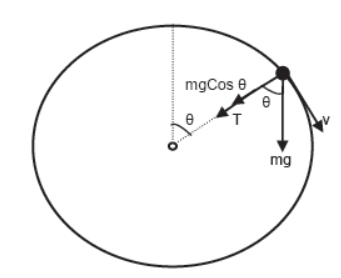
T + mgCos θ = mv2/r
For slagging T = 0,
0 + mgCos θ = mv2/r
or, v = √rgCos θ
Case-1 At Topmost point θ = 0, therefore v = √rg
Case-2 At θ = 60o, therefore v = √rgCos60 = √rg/2
Case-3 When string becomes horizontal that is at θ = 90o, v = √rgCos90 = 0
Velocity Relationship at different Points of Vertical Circular Motion
Let initial and final velocities of the body performing vertical circular motion be v1 and v2 and the angle made by string with the vertical be θ1 and θ2. Taking lowermost point of vertical circular path as reference level and applying energy conservation,
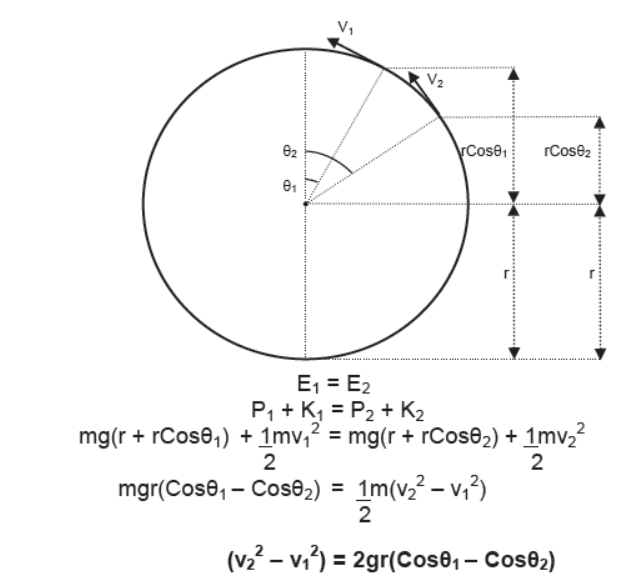
Vertical Circular Motion of a Body Attached to a Rod
Since rod can never slag hence in the critical situation a body attached to the rod may reach the topmost position A of the vertical circular path with almost zero velocity. In this case its weight mg acts in vertically downward direction and tension of rod acts on the body in the vertically upward direction. Applying net force towards center is equal to centripetal force,
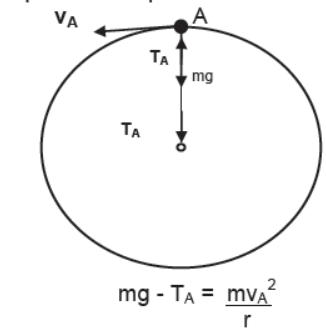
Putting vA = 0 (for critical condition)
mg – TA = 0
or, TA = mg
Critical velocity and Tension at the lower most point
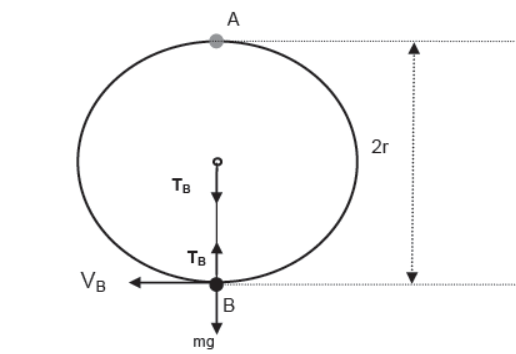
Taking B as reference level of gravitational potential energy and applying energy conservation
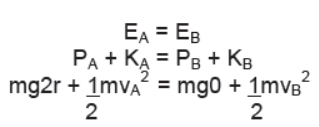

This is the minimum possible velocity at the lower most point for vertical circular motion known as critical velocity at point B.
vB(Critical) = √4rg
Tension at lowermost point in critical condition
For lowermost point B applying net force towards center is equal to centripetal force. Tension TB acts towards the center of the circular path whereas weight mg acts away from it in vertically downward direction. Hence,
Hence in critical condition of vertical circular motion of a body attached to the rod velocities at topmost and lowermost be 0 and √4rg respectively and tensions in the rod be mg (pushing nature) and 5mg (pulling nature) respectively.
Motion of A Body Over Spherical Surface
A body of mass m is moving over the surface of the smooth sphere of radius r. At any instant when the radius of sphere passing through the body makes angle θ with the vertical the tangential velocity of the body is v. Since net force towards the center is centripetal force we have
mgCosθ – N = mv2/r
or, N = mgCosθ – mv2/r
if v increases N decreases and when the body just loses contact with the sphere
N = 0.
Putting N = 0,
0 = mgCosθ – mv2/r
or, mv2 = mgCosθ/r
or, v = √rg Cosθ
This is the minimum velocity at which the body loses contact and it is the maximum velocity at which the body remains in contact with the surface.
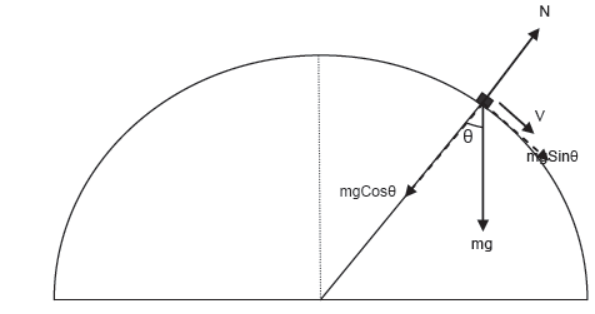
CENTRIFUGAL FORCE
It is a pseudo force experienced by a body which is a part of the circular motion. It is a non-realistic force and comes into action only when the body is in a circular motion. Once the circular motion of the body stops, this force ceases to act. Its magnitude is exactly same as that of centripetal force but it acts opposite to the direction of the centripetal force that is in the radially outward direction.
Frame of reference attached to a body moving on a circular path is a non-inertial frame since it an accelerated frame. So when ever any body is observed from this frame a pseudo force F = ma = mv2/r = mrω2 must be applied on the body opposite to the direction of acceleration along with the other forces. Since the acceleration of the frame in circular motion is centripetal acceleration a = v2/r directed towards the center of the circular path, the pseudo force applied on the bodies observed from this frame is F = mv2/r directed away from the center of the circular path. This pseudo force is termed as a centrifugal force.
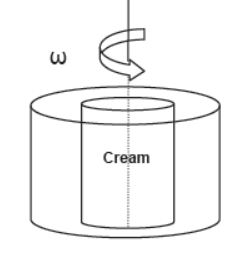
CENTRIFUGE
It is an apparatus used to separate cream from milk. It works on the principal of centrifugal force. It is a cylindrical vessel rotating with high angular velocity about its central axis. When this vessel contains milk and rotates with high angular velocity all the particles of milk start moving with the same angular velocity and start experiencing centrifugal force FCentrifugal = mrω2 in radially outward direction. Since centrifugal force is directly proportional to the mass of the particles, massive particles of milk on experiencing greater centrifugal force starts depositing on the outer edge of the vessel and lighter cream particles on experiencing smaller centrifugal force are collected near the axis from where they are separated apart.
MEMORY MAP
Critical Condition of Vertical Circular MOtion
Very Short Answer
Question. Action and reaction forces do not balance each other. Why?
Answer. Since they are acting on different bodies.
Question. The string is holding the maximum possible weight that it could withstand. What will happen to the string if the body suspended by it starts moving on a horizontal circular path and the string starts generating a cone?
Answer. It will break because tension in the string increases as soon as the body starts moving.
Question. Can a body remain in state of rest if more than one force is acting upon it?
Answer. Yes, if all the forces acting on it are in equilibrium.
Question. Is the centripetal force acting on a body performing uniform circular motion always constant?
Answer. No, only its magnitude remains constant but its direction continuously goes on changing.
Question. Is net force needed to keep a body moving with uniform velocity?
Answer. No.
Question. Is Newton’s 2nd law (F = ma) always valid. Give an example in support of your answer?
Answer. It is valid in an inertial frame of reference. In non-inertial frame of reference (such as a car moving along a circular path), Newton’s 2nd law doesn’t hold apparently.
Question. What is the maximum acceleration of a vehicle on the horizontal road? Given that coefficient of static friction between the road and the tyres of the vehicle is μ.
Answer. amax = fs(max)/m = μN/m = μmg/m = μg.
Question. Why guns are provided with the shoulder support?
Answer. So that the recoil of gun may be reduced by providing support to the gun by the shoulders.
Question. While paddling a bicycle what are the types of friction acting on rear wheels and in which direction?
Answer. Static friction in forward direction and rolling friction in backward direction.
Question. What is the reaction force of the weight of a book placed on the table?
Answer. The force with which the book attracts the earth towards it.

We hope the above Laws of Motion Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


