Question. If it is possible to make only one meaningful English word with the third, fifth, eighth and ninth letters of the word STETHOSCOPE, then which of the following will be the second letter of the word? If no such word can be made, give ‘T’ as your answer and if more than one such words can be made, give ‘M’ as your answer.
A. C
B. T
C. M
D. H
Ans.
C
Question. Select the correct mirror image of Fig. (X), if the mirror is placed vertically to the right
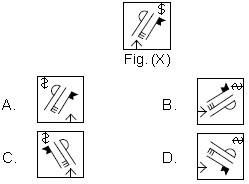
Ans.
C
Question. A word and number arrangement machine when given an input line of words and numbers rearranges them following a particular rule in each step. The following is an illustration of input and rearrangement
Input : easy 23 man 47 story 17 war 54
Step I : 17 easy 23 man 47 story war 54
Step II : 17 war easy 23 man 47 story 54
Step III : 17 war 23 easy man 47 story 54
Step IV : 17 war 23 story easy man 47 54
Step V : 17 war 23 story 47 easy man 54
Step VI : 17 war 23 story 47 man easy 54
Step VII : 17 war 23 story 47 man 54 easy
Step VII is the last step of the given input.
As per the rules followed in the given steps, which is the last step for the following input?
Input : 87 god 29 quick 72 home 65 come
A. V
B. VI
C. VII
D. IV
Ans.
B
Question. Find the number of squares in the given figure.
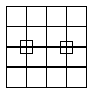
A. 28
B. 40
C. 39
D. None of these
Ans
B
Question. If ‘×’ stands for ‘greater than’, ‘–’ stands for ‘addition’, ‘÷’ stands for ‘division’, ‘+’ stands for ‘equal to’, ‘<’ stands for ‘multiplication’, ‘>’ stands for ‘less than’ and ‘=’ stands for ‘subtraction’, then which of the following options is correct?
A. 5 < 2 = 1 + 3 – 4 – 1
B. 5 = 2 – 1 + 3 < 4 – 1
C. 5 < 2 – 1 + 3 < 4 = 1
D. 5 ÷ 2 – 1 > 3 ÷ 4 < 1
Ans.
C
Question. Find the missing number from the options, if a certain rule is followed either row-wise or column-wise
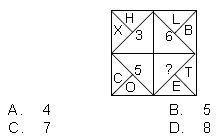
Ans.
A
Question. Study the given information carefully and answer the question that follows. P, Q, R, S, T and U are seated in a circle facing the centre. P and R are seated adjacent to each other and T and Q are also seated adjacent to each other. Q is to the immediate left of U. There are two persons between S and T. P is not seated adjacent to T. Who is seated to the immediate left of S?
A. U
B. Q
C. P
D. T
Ans.
A
Question. Select a figure from the options which will continue the same series as established by the Problem Figures.
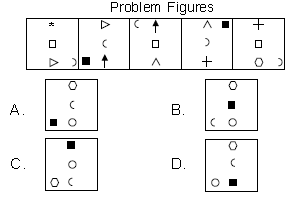
Ans.
A
Question. In a certain code language, if ‘ta ka re ma’ means ‘birds fly very high’, ‘si ma do ka’ means ‘birds are very beautiful’ and ‘ne ja re ba’ means ‘the parrots could fly’, then which letter code stands for high?
A. ta
B. re
C. ka
D. ma
Ans.
A
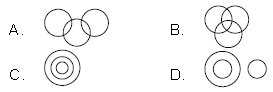
Question. Which of the following Venn diagrams best represents the relationship amongst, “Poet, Niece, Father”?
Ans.
A
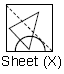
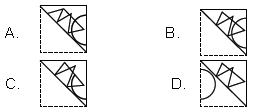
Question. A square transparent Sheet (X) with a pattern and a dotted line on it is shown here. If the sheet is folded along the dotted line, then which pattern would appear from the given options?
Ans.
B
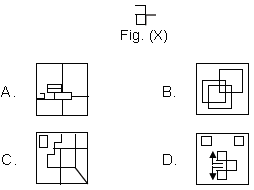
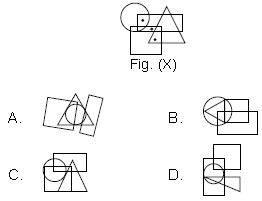
Question. In which of the following figures, Fig. (X) is exactly embedded as one of its parts?
Ans.
D
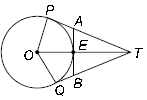
Question. In the given figure, PQR is a tangent to the circle with centre O. OQ is the radius of the circle at the point of contact R and O are joined and produced to the point S on the circle. If ∠QRO = 28°, ∠QOR = x and ∠OQS = y, then find the value of x and y respectively.
A. 31°, 31°
B. 62°, 62°
C. 62°, 31°
D. 90°, 45°
Ans.
C
Question. There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30° and 45°, find the height of the tree.
A. 35.3 m
B. 35.6 m
C. 35 m
D. 36.60 m
Ans.
D
Question. In an A.P., if S5 + S7 = 167 and S10 = 235, then find the A.P., where Sn denotes the sum of its first n terms.
A. 1, 6, 11, 16, 21,……….
B. 1, 5, 9, 13, 17,……….
C. 2, 8, 14, 20, 26,……….
D. 2, 5, 8, 11, 14,……….
Ans.
A
Question. The roots of the quadratic equation1/a + b + x = a/a + 1/b + 1/x, a + b ≠ 0 are ______.
A. a, b
B. – a, b
C. a, – b
D. – a, – b
Ans.
D
Question. Read the statements carefully and select the CORRECT option.
Statement I : TF is a tower with F on the ground. The angle of elevation of T from A is x such that tan x = 2/5 and AF = 200 m. The angle of elevation of T from a nearer point B is y with BF = 80 m. The value of y is 45°.
Statement II : The angles of elevation of the top of a tower from two points P and Q at distances m2 and n2 respectively, from the base and in the same straight line with
it are complementary. The height of the tower is m/n.
A. Both Statement I and Statement II are true.
B. Statement I is true but Statement II is false.
C. Statement I is false but Statement II is true.
D. Both Statement I and Statement II are false.
Ans.
B
Question. From a pack of 52 cards, a card is chosen at random. Find the probability that the chosen card is :
(i) A black king.
(ii) Neither a heart nor a king.
(i) (ii)
A. 1/26 7/13
B. 1/13 9/13
C. 1/13 7/13
D. 1/26 9/13
Ans.
D
Question. In the given figure (not drawn to scale), ABCD is a trapezium with AB||DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure
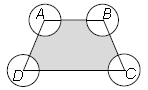
A. 196 cm2
B. 225 cm2
C. 350 cm2
D. 154 cm2
Ans.
A
Question. There is a certain relationship between figures (i) and (ii). Establish a similar relationship between figures (iii) and (iv) by selecting a suitable figure from the options which will replace the (?) in figure (iii).
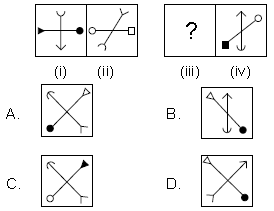
Ans.
A
Question. A point P divides the line joining the points (2, 1) and (5, –8) in ratio 1 : 2. Also, the point P lies on the line 2x – y + k = 0. Find the value of k.
A. 8
B. –8
C. –6
D. 6
Ans.
B
Question. If a and b are the zeroes of the polynomial x2 + 4x + 3, then find the polynomial whose zeroes are 1+β/α and 1+ α/β.
A. x2 + 16x + 16
B. x2 – 16x + 16
C. 3x2 – 16x + 16
D. 3x2 + 16x + 16
Ans.
C
Question. The decimal representation of 3/215 × 510 will terminate after how many places of decimals?
A. 15
B. 10
C. 5
D. None of these
Ans.
A
Question. Find the values of m and n respectively so that the following system of linear equations have infinite number of solutions.
(2m – 1)x + 3y – 5 = 0
3x + (n – 1)y – 2 = 0.
A. 11/2, 17/2
B. 17/5, 11/5
C. 17/4, 11/5
D. 17/4, 11/2
Ans.
C
Question. In a trapezium ABCD, AB||DC, DC = 2AB and EF||AB, where E and F lie on BC and AD respectively such that BE/EC = 4/3. If diagonal DB intersects EF at G, then 7EF = kAB. Find the value of k.
A. 7
B. 9
C. 10
D. 11
Ans.
D
Question. The side of solid metallic cube is 50 cm. The cube is melted and recast into 8000 equal solid cubical dice. Determine the side of the dice.
A. 2.8 cm
B. 3 cm
C. 8 cm
D. 2.5 cm
Ans.
D
Question. If 15 tan2 q + 4sec2 q = 23, then find the value of (sec q + cosec q)2 – sin2 q.
A. 13/√2
B. 13/2
C. 15/2
D. 15/√2
Ans.
C
Question. If the median for the following frequency distribution is 28.5, then find the values of x and y respectively
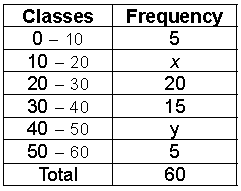
A. 8, 7
B. 7, 8
C. 9, 6
D. 6, 9
Ans.
A
Question. Evaluate [4(sin2 30° + cos4 60°) – 3(cos2 45° – sin2 90°)]
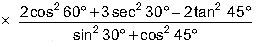
A. 55/6
B. 0
C. 1
D. 32/3
Ans.
A
Question. O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm. TP a n d TQ a r e tangents to the circle and OT intersects the circle at E.
AB is tangent to the circle at E intersecting TP and TQ at A and B respectively. Find the length of AB.
A. 6 (2/5)cm
B. 6 (2/3)cm
C. 6 (2/9)cm
D. 3 (1/3)cm
Ans.
B
Question. If the centroid of the triangle formed by the points A(a, b), B(b, c) and C(c, a) is at the origin, then what is the value of a2/bc + b2/ca + c2/ab ?
A. 0
B. a + b + c
C. 3
D. a3 + b3 + c3
Ans.
C
Question. Find the positive value of k for which quadratic equations x2 + kx + 64 = 0 and x2 – 8x + k = 0 will have real roots.
A. 16
B. –16
C. 12
D. –12
Ans.
A
Question. A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
A. 2440 m
B. 2560 m
C. 4480 m
D. 3280 m
Ans.
C
Question. What should be added in the polynomial x3 – 6x2 + 11x + 8 so that it is completely divisible by x2 – 3x + 2?
A. 2
B. –2
C. 14
D. –14
Ans.
D
Question. Which of the following statements is CORRECT?
A. A tangent to a circle is perpendicular to the radius through the point of contact.
B. A line which intersects a circle in two distinct points is called a secant of the circle.
C. The lengths of the two tangents drawn from an external point to a circle are equal.
D. All of these
Ans.
D
Question. Mohit and Rohit each have certain number of oranges. Mohit says to Rohit, ‘‘if you give me 10 of your oranges, I will have twice the number of oranges left with you’’. Rohit replies, “if you give me 10 of your oranges, I will have the same number of oranges as left with you.’’ Find the number of oranges with Mohit and Rohit respectively.
A. 50, 70
B. 70, 50
C. 60, 60
D. 80, 40
Ans.
B
Question. A shopkeeper sold an air-conditioner for ₹25935 with a discount of 9% and earned a profit of 3.74%. What would have been the percentage of profit if no discount were offered?
A. 12.3%
B. 15.6%
C. 16%
D. None of these
Ans.
D
Question. Amita, Suneha and Raghav start preparing cards for all the persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together?
A. 40 minutes
B. 50 minutes
C. 60 minutes
D. 80 minutes
Ans.
D
Question. Raghav buys a shop for ₹1,20,000. He pays half of the amount in cash and agrees to pay the balance in 12 annual instalments of ₹ 5000 each. If the rate of interest is 12% and he pays with the instalment the interest due on the unpaid amount, find the total cost of the shop.
A. ₹ 1,60,800
B. ₹ 1,66,800
C. ₹ 1,68,800
D. ₹ 1,60,000
Ans.
B
Question. A shopkeeper buys a number of books for ₹ 80. If he had bought 4 more books for the same amount, each book would have cost ₹ 1 less. How many books did he buy?
A. 16
B. 20
C. 18
D. 22
Ans.
A
Question. A child has a block in the shape of a cube with one letter written on each face as shown here:

The cube is thrown once. What is the probability of getting a vowel?
A. 5/6
B. 1
C. 1/3
D. 1/6
Ans.
C
Question. Select a figure from the options which satisfies the same conditions of placement of the dots as in Fig.(X).
Ans.
C
Question. Aditya has a clock on the wall of his home. The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
A. 1901.85 cm
B. 1940.85 cm
C. 1910.85 cm
D. 1900 cm
Ans.
C
Question. State ‘T’ for true and ‘F’ for false and select the CORRECT option.
I. If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeroes are coincident.
II. If a quadratic polynomial f(x) is not factorisable into linear factors, then it has no real zero.
III. If graph of quadratic polynomial ax2 + bx + c cuts positive direction of y-axis, then the sign of c is positive.
IV. If fourth degree polynomial is divided by a quadratic polynomial, then the degree of the remainder is 2.
I II III IV
A. F F T T
B. T T T F
C. F T T F
D. T T T T
Ans.
B
Question. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp is 3.6 m above the ground, then find the length of her shadow after 4 seconds.
A. 0.6 m
B. 2.6 m
C. 1.4 m
D. 1.6 m
Ans.
D
Question. Group the given figures into three classes on the basis of their identical properties by using each figure only once

A. 1, 2, 3; 4, 5, 8; 6, 7, 9
B. 1, 5, 6; 2, 3, 4; 7, 8, 9
C. 1, 3, 5; 2, 4, 8; 6, 7, 9
D. 1, 4, 7; 2, 5, 8; 3, 6, 9
Ans.
B
Question. Match the following.
Column-I Column-II
P. I f p o i n t s ( k , 3 ) ,(6, –2) and (–3, 4) are (i) –4
collinear, then the value of k is
Q. If the points A(7, –2), B(5, 1) and C(3, 2k) (ii) 8/3
are collinear, then the value of k is
R. If the point P(m, 3) lies on the line segment (iii) 2
joining the points A − (2/5, 6) and B(2, 8),
then the value of m is
S. The value of a for which the area of the (iv) – 3/2
triangle formed by the points A(a, 2a), B(–2, 6) and C(3,1) is 10 square units is
A. (P)→(iv), (Q)→(iii), (R)→(i), (S)→(ii)
B. (P)→(i), (Q)→(iv), (R)→(iii), (S)→(ii)
C. (P)→(i), (Q)→(iv), (R)→(ii), (S)→(iii)
D. (P)→(iv), (Q)→(iii), (R)→(ii), (S)→(i)
Ans.
A
Question. A circus tent is cylindrical upto a height of 3 m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53 m, find the total canvas used in making the tent.
A. 9735 m2
B. 9755 m2
C. 9753 m2
D. 9537 m2
Ans.
A
Question. V1, V2, V3 and V4 are the volumes of four cubes of side lengths x cm, 2x cm, 3x cm and 4x cm respectively. Some statements regarding these volumes are shown here.
(1) V1 + V2 + 2V3 < V4
(2) V1 + 4V2 + V3 < V4
(3) 2(V1 + V3) + V2 = V4
Which of the given statements is correct?
A. (1) and (2) only
B. (2) and (3) only
C. (1) and (3) only
D. (1), (2) and (3)
Ans.
D
Question. Fill in the blanks and select the CORRECT option. If D is the midpoint of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, then
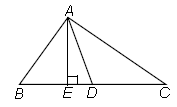
(i) b2 = p2 + P + a2/4
(ii) c2 – p2 + ax = Q
(iii) b2 + c2 = R + a2/2
P Q R
A. a2x a2/2 2p2
B. ax a2/4 4p2
C. ax a2/4 2p2
D. a2x a2/2 2p
Ans.
C


