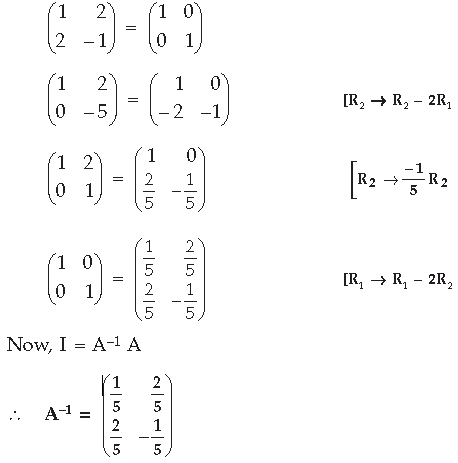Students can read the important questions given below for Matrices Class 12 Mathematics. All Matrices Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Matrices Class 12
Very Short Answer Type Questions
Question. Find the value of x from the following :
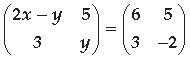
Answer.
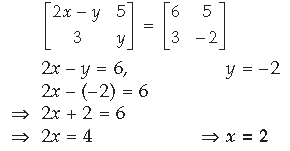
Question. Find the value of
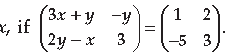
Answer.
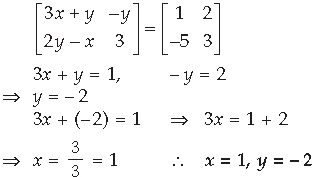
Question. If matrix A = (1 2 3), write AA′, where A′ is the transpose of matrix A.
Answer.
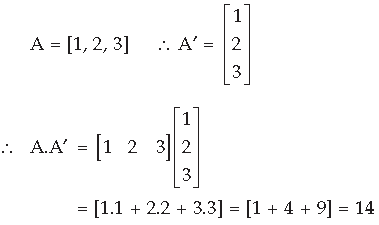
Question.
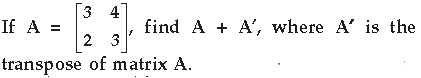
Answer.
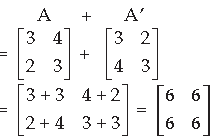
Question.
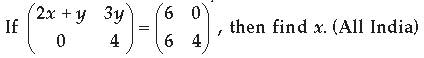
Answer.
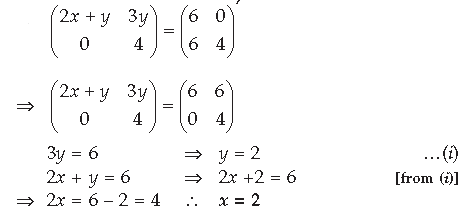
Question.
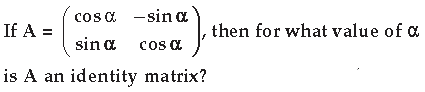
Answer. A is an identity matrix
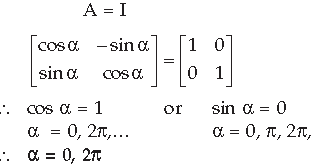
Question.
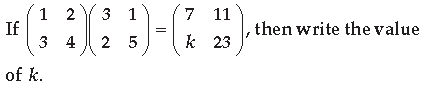
Answer.
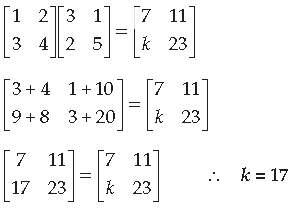
Question.
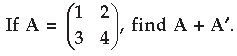
Answer. A + A′
Question. If A is a matrix of order 3 × 4 and B is a matrix of order 4 × 3, find the order of the matrix (AB).
Answer. The order of matrix A = (3 × 4)
The order of matrix B = (4 × 3)
∴ Order of matrix (AB ) = (3 × 3).
Question. Write the adjoint of the following matrix :
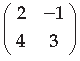
Answer.
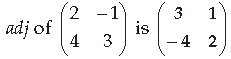
Question.

Answer.
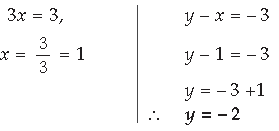
Question. If a matrix has 5 elements, write all possible orders it can have.
Answer. All possible orders are 5 × 1 and 1 × 5.
Question.
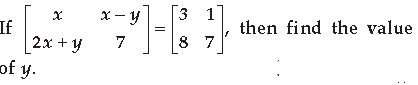
Answer.
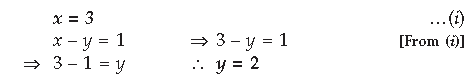
Question.
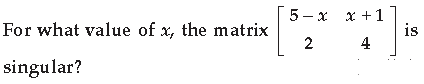
Answer.
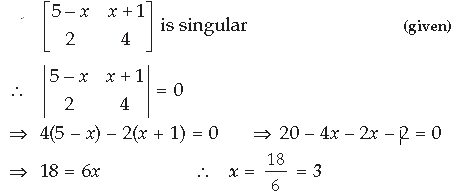
Question. Write the values of x – y + z from the following
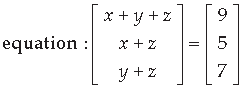
Answer. x + y + z = 9
x + z = 5 …(i)
y + z = 7
(x + z) + y = 9
5 + y = 9 [from (ii)]
y = 9 – 5 = 4 …(ii)
Now, x – y + z = (x + z) – y
= 5 – 4 = 1 [from (iii)]
Question.
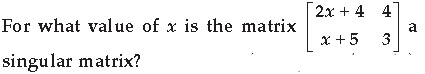
Answer.
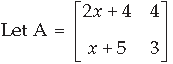
⇒ |A| = 0 [ ∴ A is a singular matrix]
⇒ 3(2x + 4) – 4(x + 5) = 0
⇒ 6x + 12 – 4x – 20 = 0
⇒ 2x = 8 ∴ x = 4
Question.
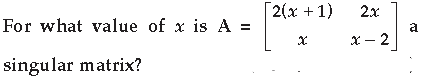
Answer.
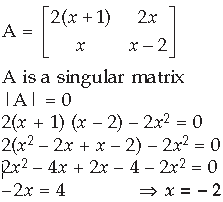
Question. For what value of y is the matrix
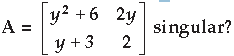
Answer.
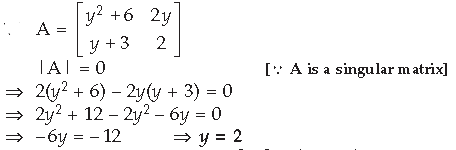
Question. For a 2×2 matrix, A = [aij], whose elements are given by aij = i/j, write the value of a12
Answer.
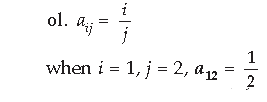
Question. Write the order of the product matrix :
Answer.
Question.
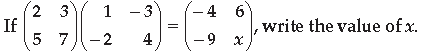
Answer.
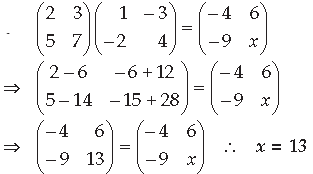
Question. Find the value of x + y from the following equation :
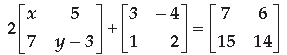
Answer.
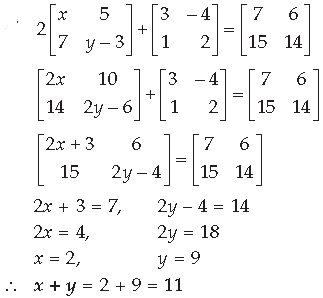
Question. Find the value of x + y from the following equation :
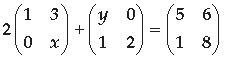
Answer.
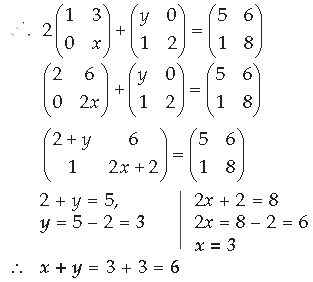
Question.
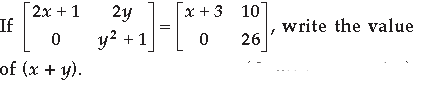
Answer.
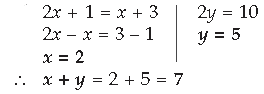
Question. Simplify :
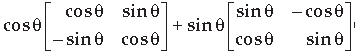
Answer.
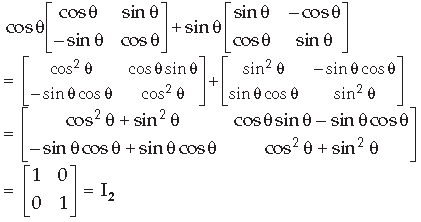
Question.
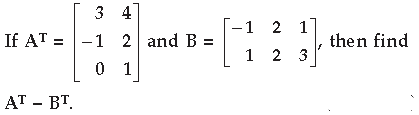
Answer.
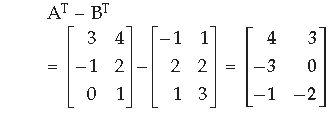
Question. For a 2×2 matrix A = [aij], whose elements are
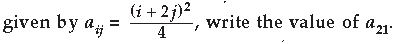
Answer.
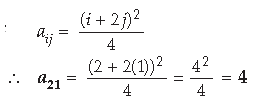
Question.
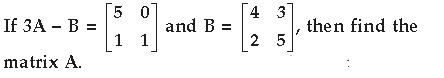
Answer.
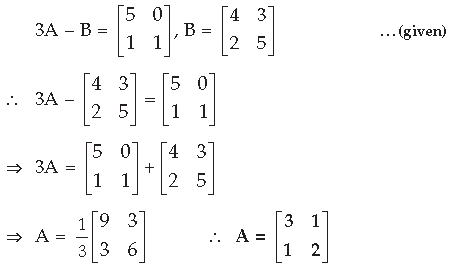
Question. Find the value of a if
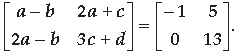
Answer. a – b = –1 ⇒ a + 1 = b …(i)
2a – b = 0
⇒ 2a – (a + 1) = 0 [From (ii)]
⇒ 2a– a – 1 = 0 ∴ a = 1
Question. For what value of x, is the matrix
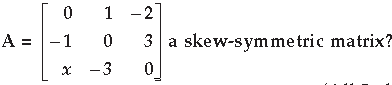
Answer. A is a skew-symmetric matrix
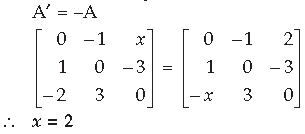
Question.
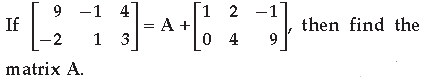
Answer.
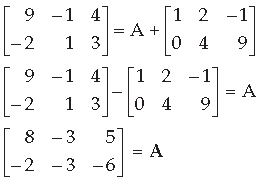
Question. For what value of x, the given matrix
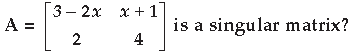
Answer.
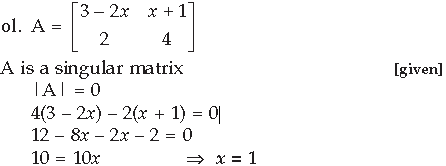
Question.
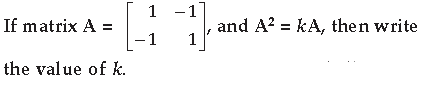
Answer. A2 = KA
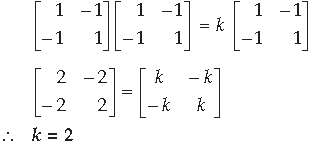
Question.
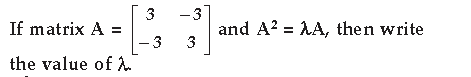
Answer. A2 = λA
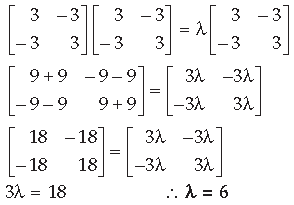
Question.
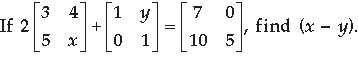
Answer.
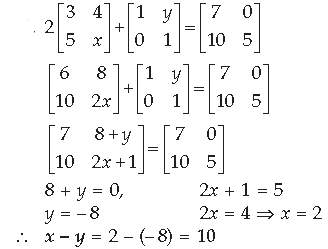
Question. Solve the following matrix equation for x :
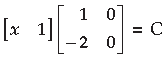
Answer.
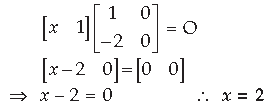
Question. If A is a square matrix such that A2 = A, then write the value of 7A – (I + A)3, where I is an identity matrix. (All India)
Answer. 7A – (I + A)3
= 7A – (I + A) (I + A) (I + A)
= 7A – (I2 + IA + AI + A2) (I + A)
= 7A – (I + A + A + A) (I + A)
[ ∵ IA = AI = A, I2 = I, A2 = A]
= 7A – (I + 3A) ( I + A)
= 7A – (I2 + IA + 3AI + 3A2)
= 7A – (I + A + 3A + 3A)
= 7A – (I + 7A)
= 7A – I – 7A = – I
Question. Write a 2×2 matrix which is both symmetric and skew-symmetric.
Answer. A matrix which is both symmetric as well as skew symmetric is a null matrix.
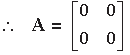
Question.
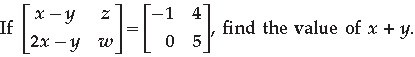
Answer.
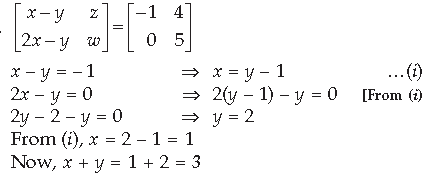
Question.
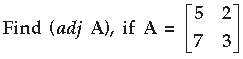
Answer.
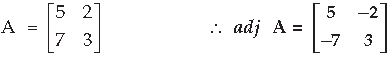
Question. The elements aij of a 3 × 3 matrix are given by aij
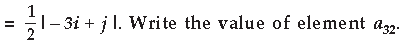
Answer.
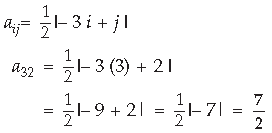
Question.
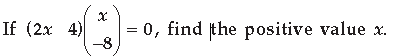
Answer.
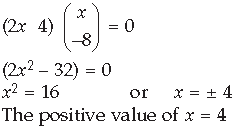
Question. Write the element a23 of a 3×3 matrix A = (aij) whose elements aij are given by aij = |i − j|/2
Answer.
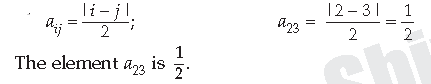
Question. In the interval π/2 < x < π, find the value of x for
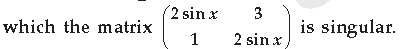
Answer.
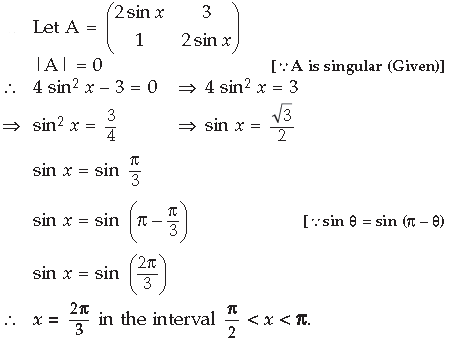
Question. If A is a square matrix such that A2 = I, then find the simplified value of (A – I)3 + (A + I)3 – 7A.
Answer. (A – I)3 + (A + I)3 – 7A
= A3 – I3 – 3A2I + 3AI2 + A3 + I3 + 3A2I + 3AI2 – 7A
…[ ∵ (a – b)3 = a3 + b3 – 3a2b + 3ab2
= 2A3 + 6AI2 – 7A
= 2A2.A + 6AI.I – 7A = 2I.A + 6A.I – 7A
= 2A + 6A – 7A = A
Question.
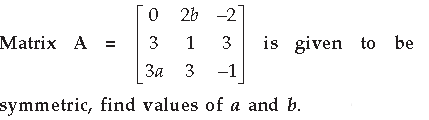
Answer. A is a symmetric matrix
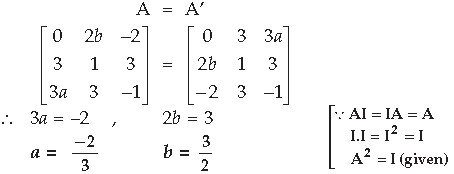
Question. Use elementary column operation C2 → C2 + 2C1 in the following matrix equation
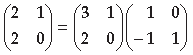
Answer.
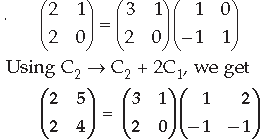
Question. Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3.
Answer. Number of possible matrices = 34 = 81.
Question.
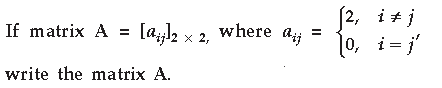
Answer.
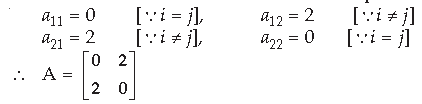
Question.
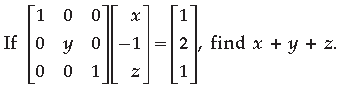
Answer.
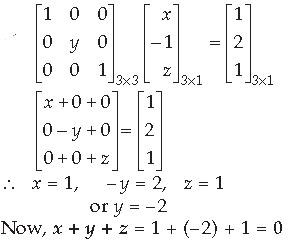
Question.
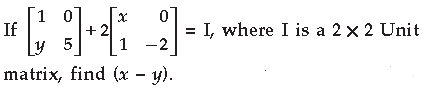
Answer.
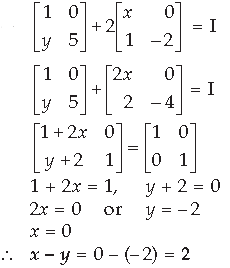
Question. Let A and B be the matrices of order 3 × 2 and 2 × 4 respectively. Write the order of matrix (AB).
Answer. The order of matrix (AB) is 3 × 4.
Short Answer Type Questions-I
Question. Show that all the diagonal elements of a skew symmetric matrix are zero.
Answer. Let A = [aij] be a skew-symmetric matrix.
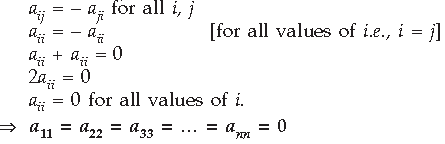
Question. In the following matrix equation use elementary operation R2 → R2 + R1 and write the equation thus obtained.
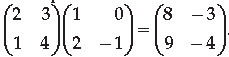
Answer.
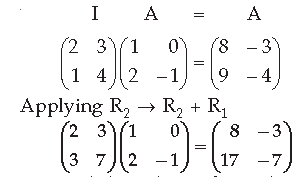
Question. Find the values of x and y from the following matrix equation :
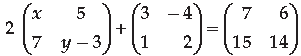
Answer.
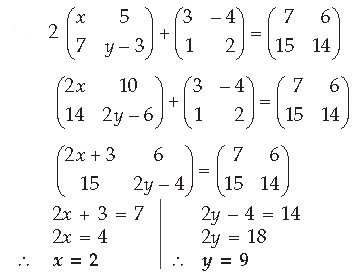
Short Answer Type Questions-II
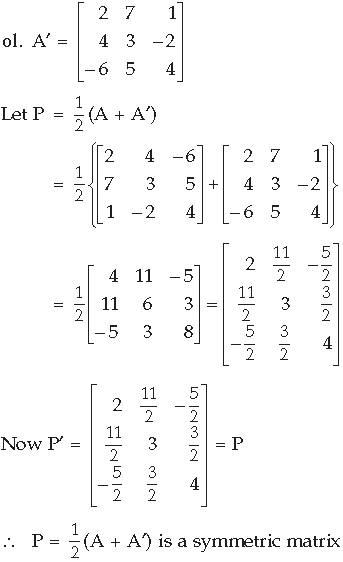
Question. Express the following matrix as the sum of a symmetric and skew symmetric matrix, and verify
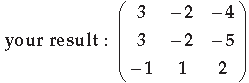
Answer.
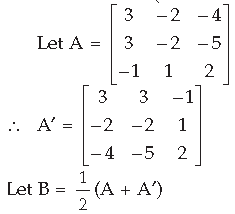


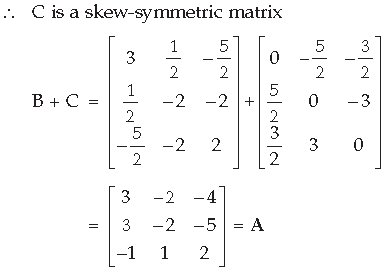
Question.
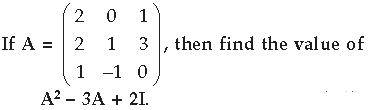
Answer.

Question. Using elementary row operations, find the inverse of the following matrix :
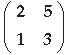
Answer.
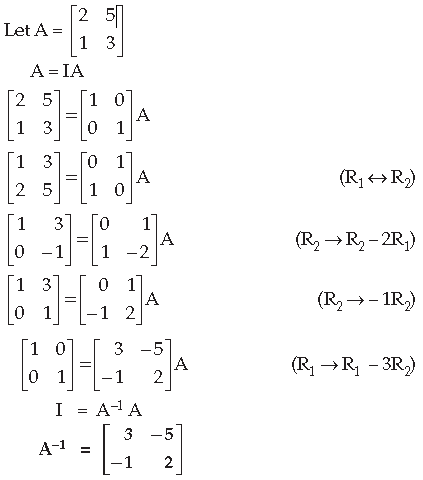
Question. For the following matrices A and B, verify that
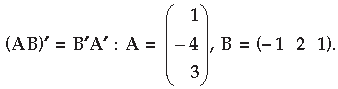
Answer.
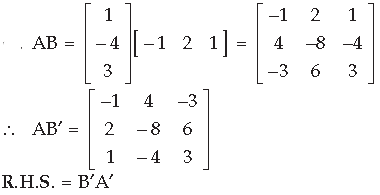
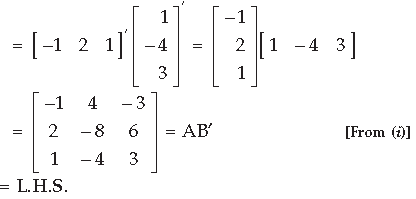
Question. Three schools A, B and C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of ₹25, ₹ 100 and ₹ 50 each. The number of articles sold are given below :
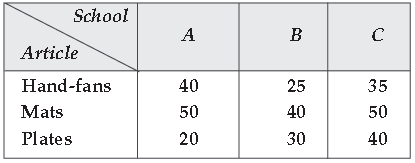
Find the funds collected by each school separately by selling the above articles. Also find the total funds collected for the purpose.
Answer. They sold handmade fans, mats and plates, at a cost of ₹25, ₹ 100 and ₹ 50 each

Question. To promote the making of toilets for women, an organisation tried to generate awareness through (i) house calls (ii) letters, and (iii) announcements. The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z are given below:
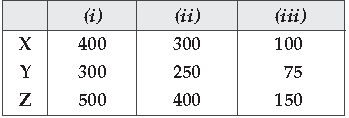
Find the total cost incurred by the organisation for the three villages separately, using matrices.
Answer. The number of attempts made in 3 villages X, Y, Z is written in Row matrix

Total cost incurred by the ogranisation for village X = ₹ 30,000
Total cost incurred by the ogranisation for village Y = ₹ 23,000
Total cost incurred by the ogranisation for village Z = ₹ 39,000
Question.
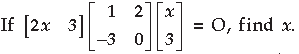
Answer.
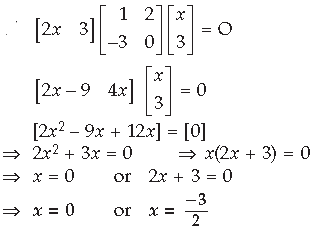
Question.
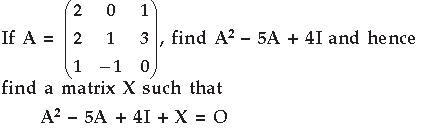
Answer. A2 – 5A + 4I
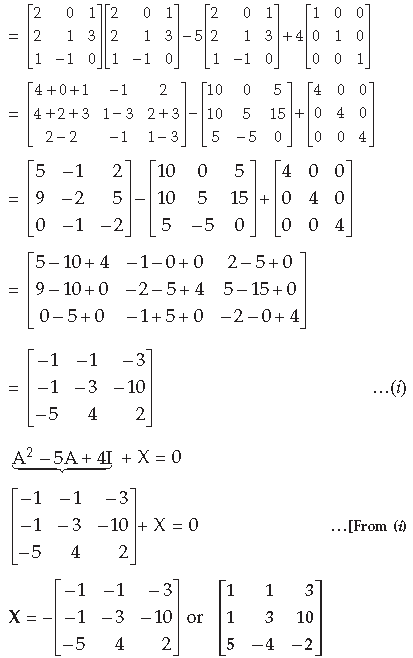
Question.
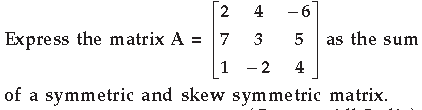
Answer.
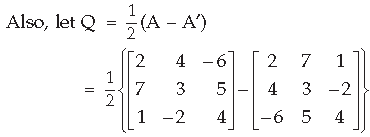

Question. Using elementary transformations, find the
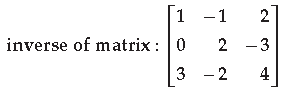
Answer.

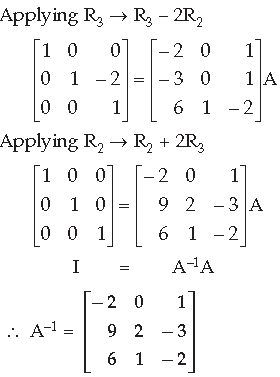
Question. A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to an orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Using matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
Answer. Let investment in first type of bonds be ₹ x and second type of bonds be ₹(35,000 – x).
Let A be the 1 × 2 matrix representing these two types

Question. To raise money for an orphanage, students of three schools A, B and C organized an exhibition in their locality, where they sold paper bags, scrap-books and pastel-sheets made by them using recycled paper at the rate of ₹ 20, ₹ 15 and ₹ 10 per unit respectively. School A sold 25 paper bags, 10 scrap-books and 30 pastel sheets. School B sold 20 paper bags, 15 scrapbooks and 30 pastel-sheets. While school C sold 25 paper bags, 18 scrap-books and 35 pastel sheets. Using matrices, find the total amount raised by each school.
Answer.

Amount raised by School A = ₹950
Amount raised by School B = ₹925
Amount raised by School C = ₹1125
Question. Two farmers X and Y cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale in rupees of these varieties of rice by both the farmers in the months of September and October are given by the following matrices A and B.
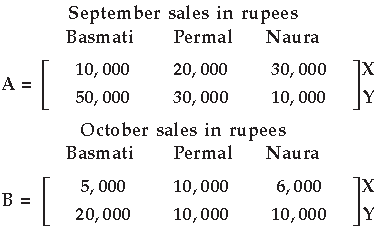
Find :
(i) What were the combined sales in September and October for each farmer in each variety?
(ii) If both farmers decided to donate 2% of the gross rupees sales in October, for the welfare of their workers, compute the total amount paid by each farmer for the welfare of the workers.
Answer.

Farmer X
Combined sales of Basmati = ₹ 15,000
Combined sales of Permal = ₹ 30,000
Combined sales of Naura = ₹ 36,000
Farmer Y
Combined sales of Basmati = ₹ 70,000
Combined sales of Permal = ₹ 40,000
Combined sales of Naura = ₹ 20,000
(ii) Donate amount
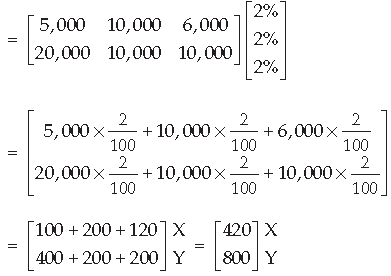
Total amount donated by X = ₹ 420
Total amount donated by Y = ₹ 800
Question.
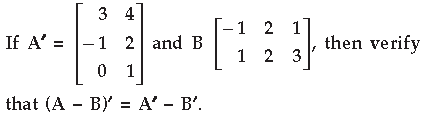
Answer.
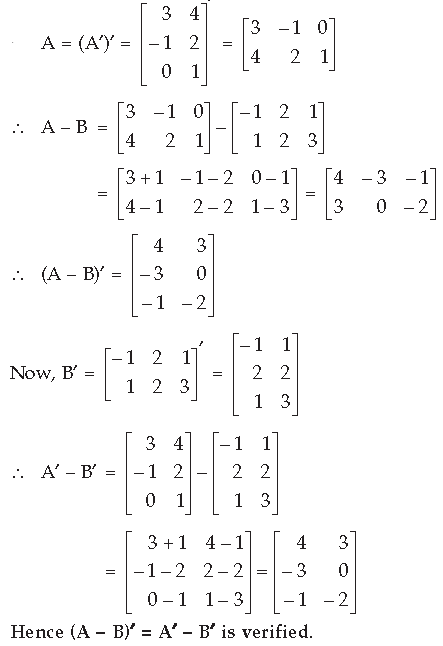
Question. Find matrix A such that
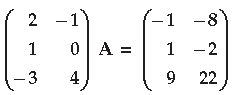
Answer.
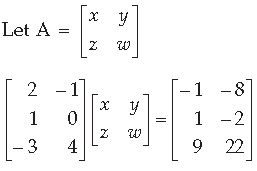
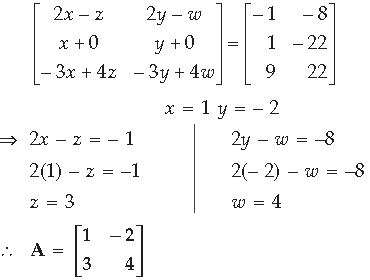
Question. Using elementary operations, find the inverse of the following matrix A
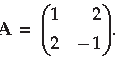
Answer.