Check the below NCERT MCQ Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Inverse Trigonometric Functions Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Inverse Trigonometric Functions Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions with solutions. Solve questions and compare with the answers provided below
Multiple Choice Questions (MCQs)
Question. Value of sin
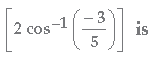
(a) − 6/5
(b) –6
(c) 24/25
(d) − 24/25
Answer
D
Question:
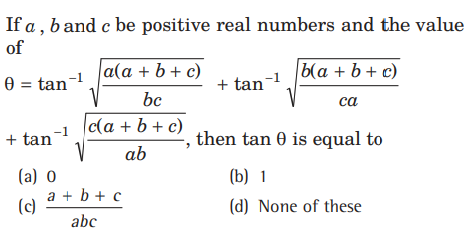
Answer
A
Question: if 3 sin-1 2x/1+x2 -4cos-1 1-x2/1+x2 +2 tan-1 2x/1-x2=π/3, then value of x is
(a) √3
(b) 1/√3
(c) 1
(d) None of these
Answer
B
Question: The sum of the infinite series cot -1 2+cot-1 8+cot-1 18+ cot-1 32+…is
(a) π
(b) π/2
(c) π/4
(d) None of these
Answer
C
Question: The value of cos ( 2cos-1 x+ sin-1x) at x =1/5 is
(a) 1
(b) 3
(c) 0
(d) -2√6/5
Answer
D
Question:
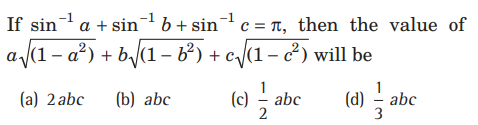
Answer
A
Question:
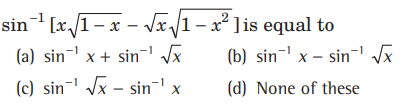
Answer
B
Question: If co-1 x+cos-1 y + cos-1 z= π, then
(a) x2 + y2 = z2
(b) x2 + y2 + z2 = 0
(c) x2 + y2 + z2 = 1-2xyz
(d) None of these
Answer
C
Question:
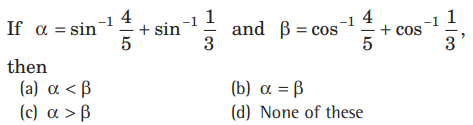
Answer
A
Question:
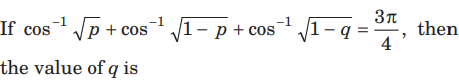
(a) 1
(b) 1/√2
(c) 1/3
(d) 1/2
Answer
D
Question:
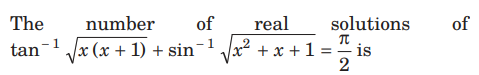
(a) 0
(b) 1
(c) 2
(d) ∞
Answer
C
Question: 4 tan -1 1/5- tan -1 1/239 is equal to
(a) π
(b) π/2
(c) π/3
(d) π/4
Answer
D
Question:
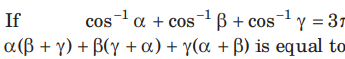
(a) 0
(b) 1
(c) 6
(d) 12
Answer
C
Question:
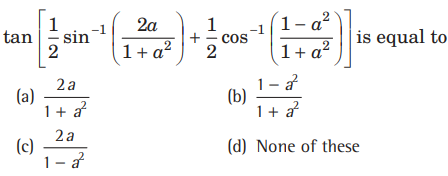
Answer
C
Question:
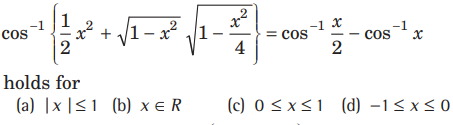
Answer
A
Question:
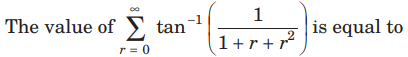
(a) π/2
(b) 3π/4
(c) π/4
(d) None of these
Answer
A
Question:
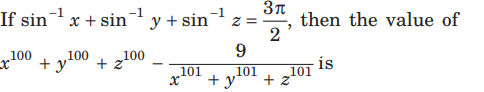
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question: If tan-1(a/x)+ tan-1(b/x)=π/2,then x is equal to
(a) √ab
(b) √2ab
(c) 2ab
(d) ab
Answer
A
Question: The value of the expression tan(1/2 cos -1 2/√5) is
(a) 2 √5
(b) √5-2
(c) √5+2
(d) 5+√2
Answer
B
Question:
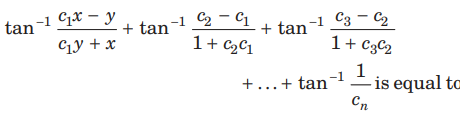

Answer
C
Question:
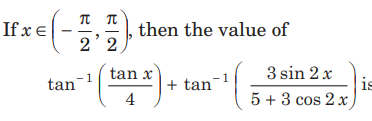
(a) x/2
(b) 2x
(c) 3x
(d) x
Answer
D
Question: If tan-1(x-1/x+2)+ tan-1 (x+1/x+2)=π/4, then x is equal to
(a) 1/√2
(b) -1/√2
(c) ±√5/2
(d) ±1/2
Answer
C
Question: If tan θ +tan (π/3+θ) +tan (-π/3+θ )=a tan 3θ,then a is equal to
(a) 1/3
(b) 1
(c) 3
(d) None of these
Answer
C
Question: The value of cot-1(xy+1/x-y) +cot-1(yz+1/y-z)+cot-1(zx+1/z-x) is
(a) 0
(b) 1
(c) cot-1 x+cot-1y +cot-1 z
(d) None of the above
Answer
A
Question: The value of the expression sin(2 tan-1 1/3) + cos (tan-1 2√2)
a) 13/15
(b) 14/15
(c) 11/15
(d) None of these
Answer
B
Question: If in a Δ ABC, ∠A =tan -12 and ∠B= tan -13, then ∠C is equal to
(a) π/2
(b) π/3
(c) π/4
(d) None of these
Answer
C
Question:

(a) 0
(b) 1
(c) 2
(d) infinite
Answer
A
Question: If 2 tan-1 (cos x) = tan-1 (2cosec x), then the value of x is
(a) 3π/4
(b) π/4
(c) π/3
(d) None of these
Answer
B
Question. If tan–1 x + tan–1 y = 4π/5, then cot–1 x + cot–1 y equals
(a) π/5
(b) 2π/5
(c) 3π/5
(d) p
Answer
A
Question.

Answer
A
Question. The principle value of the expression cos–1[cos(–680°)] is
(a) 2π/9
(b) − 2π/9
(c) 34π/9
(d) π/9
Answer
A
Question. The value of tan–1 3 – sec–1 (–2) is

Answer
C
Question.

Answer
B
Question. The value of


Answer
C
Question.

Answer
B
Case Based Questions
The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. ‘A’ is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby, Ram Robert and Rahim suggested to the film to place the hoarding board at three different locations namely C, D and E. ‘C’ is at the height of 10 metres from the ground level. For the viewer ‘A’, the angle of elevation of ‘D’ is double the angle of elevation of ‘C’. The angle of elevation of ‘E’ is triple the angle of elevation of ‘C’ for the same viewer.
Look at the figure given and based on the above information answer the following:

Question. Measure of ∠EAB
(a) tan–1 (11)
(b) tan–1 (3)
(c) tan–1 (2/11)
(d) tan–1 (11/2)
Answer
D
Question. Measure of ∠CAB =
(a) tan–1 (2)
(b) tan–1 (1/2)
(c) tan–1 (1)
(d) tan–1 (3)
Answer
B
Question. Measure of ∠DAB =
(a) tan–1 3/4
(b) tan–1(3)
(c) tan–1 (4/3)
(d) tan–1(4)
Answer
C
Question. A’ is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between ∠CAB and ∠CA’B is
(a) tan–1 (1/12)
(b) tan–1 (2/8
(c) tan–1 (2/5)
(d) tan–1 (11/25)
Answer
A
Question. Domain and Range of tan–1 x =

Answer
C
Two men on either side of a temple of 30 meters high observe its top at the angles of elevation a and β respectively (as shown in the given figure). The distance between the two men is 40√3 meters and the distance between the first person A and the temple is 30√3 meters.
Based on the above information answer the following:

Question. ∠CAB = a =

Answer
B
Question. ∠CAB = a =

Answer
C
Question. ∠BCA = β =
(a) tan–1 (1/2)
(b) tan–1 (2)
(c) tan–1(1/√3)
(d) tan–1 (√3)
Answer
D
Question. ∠ABC =
(a) π/4
(b) π/6
(c) π/2
(d) π/3
Answer
C
Question. Domain and Range of cos–1 x =
(a) (1, 1), (0, p)
(b) [–1, –1], [0, p]
(c) [–1, 1], [0, p]

Answer
C
If f (x) = sin–1 x
Based on the above function answer the following question:
Question. If function is f(–x) then equal to
(a) –f(x)
(b) f(x)
(c) cos f(–x)
(d) None of these
Answer
A
Question. If λ(x) = 2x/2+x2, then f [λ(x)] is equal to

Answer
B
Question. f(x) is equal x to
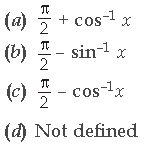
Answer
C
Question. f(x) is
(a) Odd
(b) Even
(c) Neither odd nor even
(d) not defined
Answer
A

Based on the above function answer the following question:
Question. f(x) is equal to

Answer
D
Question. Maximum value of f(x)
(a) [–1, 1]
(b) [0, ∞)
(c) (–∞, 0]
(d) not maxima
Sol. (d) not maxima
Answer
D
Question. f(x) is equal to

Answer
C
Question. f(x) is equal to

Answer
C
Question. f(x) is equal to

Answer
B
Question. Which of the following is the principal value branch of cosec-1 x?
(a) (−π/2, π/2)
(b) (0, π) – {π/2}
(c) [−π/2, π/2]
(d) [−π/2, π/2] – [0]
Answer
D
Question. If 3 tan-1 x + cot-1 x = π, then x equals
(a) 0
(b) 1
(c) -1
(d) 12
Answer
B
Question. The value of cos-1[cos(33π/5)] is
(a) 3π/5
(b) −3π/5
(c) π/10
(d) –π/10
Answer
A
Question. The domain of the function cos-1 (2x – 1) is
(a) [0, 1]
(b) [-1, 1]
(c) [-1, -1]
(d) [0, π]
Answer
A
Question. The domain of the function defined by f (x) = sin-1 √(x−1) is
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) None of these
Answer
Question. If cos(sin-12/5 + cos-1 x) = 0 then x is equal to
(a) 1/5
(b) 2/5
(c) 0
(d) 1
Answer
B
Question. The value of sin (2 tan-1 (0.75)) is equal to
(a) 0.75
(b) 1.5
(c) 0.96
(d) sin (1.5)
Answer
C
Question. The value of cos-1 (cos3π/2) is equal to
(a) π/2
(b) 3π/2
(c) 5π/2
(d) –7π/2
Answer
A
Question. The value of expression 2 sec-1 (2) + sin-1 (1/2) is
(a) π/6
(b) 5π/6
(c) 7π/6
(d) 1
Answer
B
Question. If sin-1(2a/1+a2) + cos-1(1−a2/1+a2) = tan-1(2x/1−x2) where a, x ∈ |0, 1| then the value of x is
(a) 0
(b) a2
(c) a
(d) 2a/1−a2
Answer
D
Question. The value of sin [cos-1(7/25)] is
(a) 25/24
(b) 25/7
(c) 24/25
(d) 7/24
Answer
C
Question. sin-1(−1/2)
(a) π/3
(b) –π/3
(c) π/6
(d) –π/6
Answer
D
Question. sec-1(−2/√3)
(a) π/6
(b) π/3
(c) 5π/6
(d) –2π/3
Answer
C
Question. cos-1(1/2)
(a) –π/3
(b) π/3
(c) π/2
(d) 2π/3
Answer
Question. cosec-1(−2/√3)
(a) –π/3
(b) π/3
(c) π/2
(d) –π/2
Answer
A
Question. cot-1(1)
(a) π/3
(b) π/4
(c) π/2
(d) 0
Answer
B
Question. cos-1(√3/2)
(a) 5π/6
(b) π/6
(c) 4π/9
(d) 2π/3
Answer
A
Question. cosec-1(2)
(a) π/6
(b) 2π/3
(c) 5π/6
(d) 0
Answer
A
Question. sec-1(2)
(a) π/6
(b) π/3
(c) 2π/3
(d) 5π/6
Answer
B
Question. tan-1(√3)
(a) π/6
(b) π/3
(c) 2π/3
(d) 5π/6
Answer
B
Question. cot-1(-√3)
(a) 5π/6
(b) π/3
(c) π/2
(d) π/4
Answer
A
Question. tan-1 (√3) + sec-1 (-2) – cosec-1(2/√3)
(a) 5π/6
(b) 2π/3
(c) π/3
(d) 0
Answer
D
Question. cos-1 (−1/2) + 2sin-1 (−1/2)
(a) π/3
(b) 2π/3
(c) 3π/4
(d) 5π/8
Answer
A