Check the below NCERT MCQ Class 12 Mathematics Chapter 3 Matrices with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Matrices Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Matrices Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 3 Matrices with solutions. Solve questions and compare with the answers provided below
Case Based Question
In a city there are two factories A and B. Each factory produces sports clothes for boys and girls. There are three types of clothes produced in both the factories type I, II and III. For boys the number of units of types I, II and III respectively are 80, 70 and 65 in factory A and 85, 65 and 72 are in factory B. For girls the number of units of types I, II and III respectively are 80, 75, 90 in factory A and 50, 55, 80 are in factory B.

Based on the above information, answer the following questions:
Question. If Q represents the matrix of number of units of each type produced by factory B for both boys and girls, then Q is given by

Answer
A
Question. If P represents the matrix of number of units of each type produced by factory A for both boys and girls, then P is given by

Answer
D
Question. The total production of sports clothes of each type for boys is given by the matrix

Answer
C
Question. Let R be a 3 × 2 matrix that represent the total production of sports clothes of each type for boys and girls, then transpose of R is

Answer
A
Question. The total production of sports clothes of each type for girls is given by the matrix __ .

Answer
A
A trust fund has `35,000 that must be invested in two different types of bonds, say X and Y. The first bond pays 10% interest p.a. which will be given to an old age home and second one pays 8% interest p.a. which will be given to WWA (Women Welfare Assocation). Let A be a 1 × 2 matrix and B be a 2 × 1 matrix, representing the investment and interest rate on each bond respectively.

Based on the above information, answer the following questions:
Question. If ₹15,000 is invested in bond X, then

Answer
B
Question. The total amount of interest on both bonds is given by
(a) AB
(b) A’B
(c) B′A
(b) None of these
Answer
A
Question. If ₹15,000 is invested in bond X, then total amount of interest received on both bonds is
(a) ₹2,000
(b) ₹2,100
(c) ₹3,100
(d) ₹4,000
Answer
C
Question. If the amount of interest given to Old age home is ₹500, then the amount of investment in bond Y is
(a) ₹20,000
(b) ₹30,000
(c) ₹15,000
(b) ₹25,000
Answer
B
Question. If the trust fund obtains an annual total interest of ₹3,200, then the investment in two bonds is
(a) ₹15,000 in X, ₹20,000 in Y
(b) ₹17,000 in X, ₹18,000 in Y
(c) ₹20,000 in X, ₹15,000 in Y
(d) ₹18,000 in X, ₹17,000 in Y
Answer
C
Two farmers Shyam and Balwan cultivate only varieties of pulses namely Urad, Masoor and Mung. The sale (in `) of these varieties of pulses by both the farmers in the month of September and October are given by the following matrices A and B.

Using algebra of matrices, answer the following questions.
Question. The combined sales of Masoor in September and October, for farmer Balwan singh, is
(a) ₹80,000
(b) ₹90,000
(c) ₹40,000
(d) ₹1,35,000
Answer
C
Question. Find the decrease in sales of Mung from September to October, for the farmer Shyam is
(a) ₹24,000
(b) ₹10,000
(c) ₹30,000
(d) No change
Answer
A
Question. The combined sales of Urad in September and October, for farmer Shyam is
(a) ₹20,000
(b) ₹30,000
(c) ₹36,000
(d) ₹15,000
Answer
D
Question. Which variety of pulse has the highest selling value in the month of September for the farmer Balwan Singh?
(a) Urad
(b) Masoor
(c) Mung
(d) All of these have the same price
Answer
A
Question. If both farmers receive 2% profit on gross sales, compute the profit for each farmer and for each variety sold in October.
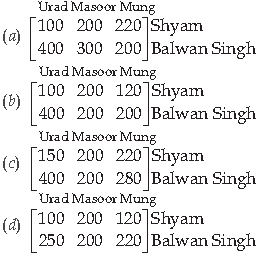
Answer
B
If A = [aij]m × n and B = [bij]m × n are two matrices, then A ± B is of order m × n and is defined as (A ± B)ij = aij + bij, where i = 1, 2,…, m and j = 1, 2, …., n If A = [aij]m × n and B = [bjk]n × p are two matrices, then AB is of order m × p and is defined as
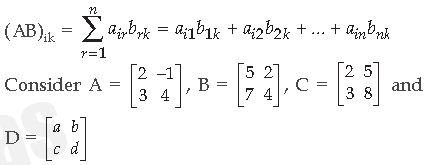
Using the concept of matrices answer the following questions:
Question. Find the product AB.
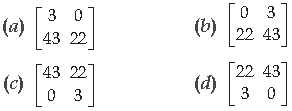
Answer
A
Question. Find the values of a and c in the matrix D such than CD – AB = 0.
(a) a = 77, c = –191
(b) a = –191, c = 77
(c) a = 191, c = 77
(d) a = 91, c = 70
Answer
B
Question. If A and B are any other two matrices such that AB exists, then
(a) BA does not exist
(b) BA will be equal to AB
(c) BA may or may not exist
(d) None of these
Answer
C
Question. Find B + D.

Answer
D
Question. Find the values of b and d in the matrix D such that CD – AB = 0.
(a) b = 44, d = –110 (
b) b = –110, d = –44
(c) b = –110, d = 44
(d) b = –44, d = 110
Answer
C
Three shopkeepers A, B and C go to a store to buy stationary. A purchase 12 dozen notebooks, 5 dozen pens and 6 dozen pencils. B purchases 10 dozen notebooks, 6 dozen pens and 7 dozen pencils. C purchases 11 dozen notebooks, 13 dozen pens and 8 dozen pencils. A notebook costs ₹40, a pen costs ₹12 and a pencil costs ₹3.

Based on the above information, answer the following questions:
Question. If Y represents the matrix formed by the cost of each item, then XY equals

Answer
B
Question. The number of items purchased by shopkeepers A, B and C represented in matrix form as

Answer
A
Question. Bill of A is equal to
(a) ₹6740
(b) ₹8140
(c) ₹3740
(d) ₹6696
Answer
D
Question. If A and B are 3 × matrices such that A2 – B2 = (A – B) (A + B), then
(a) either A or B is zero matrix
(b) either A or B is unit matrix
(c) A – B
(d) AB = BA
Answer
D
Question. If A2 = A, then (A + I)3 – 7A =
(a) A
(b) A – I
(c) I
(d) A + I
Answer
C
A manufacture produces three stationery products—Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below:

If the unit Sale price of Pencil, Eraser and Sharpener are ₹2.50, ₹1.50 and ₹1.00 respectively, and unit cost of the above three commodities are ₹2.00, ₹1.00 and ₹0.50 respectively, then
Based on the above information answer the following:
Question. Total Revenue of Market A
(a) ₹64,000
(b) ₹60,400
(c) ₹46,000
(d) ₹40,600
Answer
C
Question. Gross Profit in both markets
(a) ₹23,000
(b) ₹20,300
(c) ₹32,000
(d) ₹30,200
Answer
C
Question. Total Revenue of Market B
(a) ₹35,000
(b) ₹53,000
(c) ₹50,300
(d) ₹30,500
Answer
B
Question. Profit in Market A and B respectively are
(a) ₹15,000, ₹17,000
(b) ₹17,000, ₹15,000
(c) ₹51,000, ₹71,000
(d) ₹10,000, ₹20,000
Answer
A
Question. Cost incurred in Market A
(a) ₹13,000
(b) ₹30,100
(c) ₹10,300
(d) ₹31,000
Answer
D
Amit, Biraj and Chirag were given the task of creating a square matrix of order 2. Below are the matrices created by them. A, B, C are the matrices created by Amit, Biraj and Chirag respectively.

If a = 4 and b = –2, based on the above information answer the following

Question. Sum of the matrices A, B and C, A + (B + C) is

Answer
C
Question. AC – BC is equal to
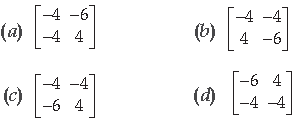
Answer
C
Question. (AT)T is equal to

Answer
A
Question. (a + b) B is equal to

Answer
C
Question. (bA)T is equal to
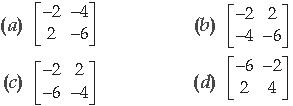
Answer
B
Three schools DPS, CVC and KVS decided to organise a fair for collecting money for helping the flood victims. They sold handmade fans, mats and plates from recycled material at a cost of ₹25, ₹100 and ₹50 each respectively. The numbers of articles sold are given as

Based on the information given above, answer the following questions:
Question. What is the total money (in ₹) collected by the school DPS?
(a) 700
(b) 7,000
(c) 6,125
(d) 7,875
Answer
B
Question. If the number of handmade fans and plates are interchanged for all the schools, then what is the total money collected by all schools?
(a) ₹18000
(b) ₹6,750
(c) ₹5000
(d) ₹21,250
Answer
D
Question. What is the total amount of money collected by all three schools DPS, CVC and KVS?
(a) ₹15,775
(b) ₹14,000
(c) ₹21,000
(d) ₹17,125
Answer
C
Question. How many articles (in total) are sold by three schools
(a) 230
(b) 130
(c) 430
(d) 330
Answer
D
Question. What is the total amount of money (in ₹) collected by schools CVC and KVS?
(a) 14,000
(b) 15,725
(c) 21,000
(d) 13,125
Answer
A
On her birthday, Seema decided to donate some money to children of an orphanage home. If there were 8 children less, everyone would have got ₹10 more. However, if there were 16 children more, everyone would have got ₹10 less. Let the number of children be x and the amount distributed by Seema for one child be y (in ₹).

Based on the given information, answer the following questions:
Question. How much amount is given to each child by Seema?
(a) ₹32
(b) ₹30
(c) ₹62
(d) ₹26
Answer
B
Question. The equations in terms x and y are
(a) 5x – 4y = 40
5x – 8y = –80
(b) 5x – 4y = 40
5x – 8y = 80
(c) 5x – 4y = 40
5x + 8y = –80
(d) 5x + 4y = 40
5x + 8y = –80
Answer
A
Question. The number of children who were given some money by Seema, is
(a) 30
(b) 40
(c) 23
(d) 32
Answer
D
Question. How much amount Seema spends in distributing the money to all the students of the Orphanage?
(a) ₹609
(b) ₹960
(c) ₹906
(d) ₹690
Answer
B
Question. Which of the following matrix equations represent the given information?

Answer
C
Two farmers Ramakishan and Gurucharan Singh cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale (in ₹) of these varieties of rice by both the farmers in the month of September and October are given by the following matrices A and B.

Question. If Gurucharan receives 2% profit on gross sales, compute his profit for each variety sold in September.
(a) ₹100, ₹200 and ₹120
(b) ₹1000, ₹600 and ₹200
(c) ₹400, ₹200 and ₹120
(d) ₹1200, ₹200 and ₹120
Answer
B
Question. What is the value of A23?
(a) 10,000
(b) 20,000
(c) 30,000
(b) 40,000
Answer
A
Question. The decrease in sales from September to October is given by _______
(a) A + B
(b) A – B
(c) A > B
(d) A < B
Answer
B
Question. The total sales in September and October for each farmer in each variety can be represented as _______
(a) A + B
(b) A – B
(c) A > B
(b) A < B
Answer
A
Question. If Ramakishan receives 2% profit on gross sales, compute his profit for each variety sold in October.
(a) ₹100, ₹200 and ₹120
(b) ₹100, ₹200 and ₹130
(c) ₹100, ₹220 and ₹120
(d) ₹110, ₹200 and ₹120
Answer
A
Manjit wants to donate a rectangular plot of land for a school in his village. When he was asked to give dimensions of the plot, he told that if its length is decreased by 50 m and breadth is increased by 50 m, then its area will remain same, but if length is decreased by 10 m and breadth is decreased by 20 m, then its area will decrease by 5300 m2.
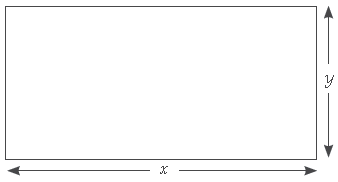
Based on the information given above, answer the following questions:
Question. Which of the following matrix equation is represented by the given information.

Answer
A
Question. The equations in terms of x and y are
(a) x – y = 50, 2x – y = 550
(b) x – 10y = 50, 2x + y = 550
(c) x + y = 50, 2x + y = 550
(d) x + y = 50, 2x + y = 550
Answer
B
Question. How much is the area of rectangular field?
(a) 60,000 sq. m.
(b) 30,000 sq. m.
(c) 30,000 m
(d) 3,000 m.
Answer
B
Question. The value of x (length of rectangular field) is.
(a) 150 m
(b) 400 m
(c) 200 m
(d) 320 m
Answer
C
Question. The value of y (breadth of rectangular field) is.
(a) 150 m
(b) 200 m
(c) 430 m
(d) 350 m
Answer
A


