MCQ Question for Class 12 Mathematics Chapter 6 Application of Derivatives

Check the below NCERT MCQ Class 12 Mathematics Chapter 6 Application of Derivatives with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Application of Derivatives Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams

Application of Derivatives Class 12 Mathematics MCQ Questions with Answers

Refer below for MCQ Class 12 Mathematics Chapter 6 Application of Derivatives with solutions. Solve questions and compare with the answers provided below

Question. A particle moves along the curve 6y = x³ + 2. The point ‘P’ on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate, are (4, 11) and (-4 , -31/3) .
(a) x-coordinates at the point P are ± 4
(b) y-coordinates at the point P are 11 and -31/3
(c) Both (a) and (b)
(d) None of the above

Question. The difference between the greatest and least values of the function f(x) = sin²x – x, on [-π/2 , π/2] is
(a) π/2
(b) π
(c) 3π
(d) π/4 

Question. The slope of the normal to the curve
(a) x = a cos³θ, y = a sin³θ at θ = π/4 is 0
(b) x = 1 – a sinθ, y = b cos²θ at θ = π/2 is a/2b
(c) Both (a) and (b) are true
(d) Both (a) and (b) are not true

Question. The two curves x³ – 3xy² + 2 = 0 and 3x²y – y³ – 2 = 0 intersect at an angle of
(a) π/4
(b) π/3
(c) π/2
(d) π/6

Question. The maximum area of rectangle inscribed in a circle of diameter R is
(a) R²
(b) R²/2
(c) R²/4
(d) R²/8

Question. If I be an open interval contained in the domain of a real valued function f and if x₁ < x₂ in I, then which of the following statements is true?
(a) f is said to be increasing on I, if f(x₁) ≤ f(x₂) for all x₁, x₂ < I
(b) f is said to be strictly increasing on I, if f(x₁) < f(x₂) for all x₁, x₂ < I
(c) Both (a) and (b) are true
(d) Both (a) and (b) are false

Question. If sum of two numbers is 3, the maximum value of the product of first and the square of second is
(a) 4
(b) 3
(c) 2
(d) 1

Question. If f(x) = x³ – 7x² + 15, then the approximate value of f(5.001) is
(a) 34.995
(b) – 30.995
(c) 24.875
(d) None of these

Question. If the error committed in measuring the radius of sphere, then … will be the percentage error in the surface area.
(a) 1%
(b) 2%
(c) 3%
(d) 4%

Question. If f be a function defined on an interval I and there exists a point c in I such that f(c) > f(x), for all x ∈ I, then
(a) function ‘f’ is said to have a maximum value in I
(b) the number f(c) is called the maximum value of f in I
(c) the point c is called a point of maximum value of f in I
(d) All the above are true

Question. What is the interval in which the function f (x) = √9-x² is increasing? (f (x)>0)
(a) 0 < x < 3
(b) – 3 < x < 0
(c) 0 < x < 9
(d) – 3 < x < 3

Question. Test to examine local maxima and local minima of a given function is/are
(a) first derivative test
(b) second derivative test
(c) Both (a) and (b)
(d) None of these

Question. If at x = 1, the function x4 – 62x² + ax + 9 attains its maximum value on the interval [0, 2], then the value of a is
(a) 110
(b) 10
(c) 55
(d) None of these

Question. The maximum value of In x/x in (2 , ∞) is
(a) 1
(b) e
(c) 2/e
(d) 1/e

Question. The maximum value of (1/x)x is
(a) e
(b) e^e
(c) e^1/e
(d) (1/e)1/e

Question. The angle of intersection to the curve y = x², 6y = 7 – x³ at (1, 1) is :
(a) π/2 
(b) π/4
(c) π/3
(d) π

Question. If for a function f (x), f ‘(a) = 0, f “(a) = 0, f ”'(a) > 0, then at x = a, f (x) is
(a) Minimum
(b) Maximum
(c) Not an extreme point
(d) Extreme point

Question. The normal to a given curve is parallel to x-axis if
(a) dy/dx = 0
(b) dy/dx = 1
(c) dy/dx = 0
(d) dy/dx = 1

Question. If y = (4x – 5) is a tangent to the curve y² = px³ + q at (2, 3), then
(a) p = – 2, q = – 7
(b) p = – 2, q = 7
(c) p = 2, q = – 7
(d) p = 2, q = 7

Question. The radius of a sphere initially at zero increases at the rate of 5 cm/sec. Then its volume after 1 sec is increasing at the rate of :
(a) 50 π
(b) 5 π
(c) 500 π
(d) None of these

Question. The interval in which the function f(x) = 4×2 + 1/x is decreasing is :
(a) (-1/2 , 1/2)
(b) [-1/2 , 1/2]
(c) (–1, 1)
(d) [–1, 1]

Question. The function f (x) = x² –2x is strictly increasing in the interval:
(a) (–2, –1)
(b) (–1, 0)
(c) (0, 1)
(d) (1, 2)

Question. The slope of the tangent to the curve x = 3t² + 1, y= t³ –1 at x = 1 is:
(a) 1/2
(b) 0
(c) –2
(d) ∞

Question. The volume V and depth x of water in a vessel are connected by the relation V = 5x – x²/6 and the volume of water is increasing , at the rate of 5 cm3/sec, when x = 2 cm. The rate at which the depth of water is increasing, is
(a) 5/18 cm / sec
(b) 1/4 cm / sec
(c) 5/16 cm / sec
(d) None of these

Question. The curve given by x + y = exy has a tangent parallel to the Y-axis at the point
(a) (0, 1)
(b) (1, 0)
(c) (1, 1)
(d) None of these

Question. What is the x-coordinate of the point on the curve f (x) = √x (7x – 6), where the tangent is parallel to x-axis?
(a) -1/3
(b) 2/7
(c) 6/7
(d) 1/2

Question. The radius of a cylinder is increasing at the rate of 3 m/s and its altitude is decreasing at the rate of 4 m/s. The rate of change of volume when radius is 4 m and altitude is 6m, is
(a) 20 π m³/s
(b) 40 π m³/s
(c) 60 π m³/s
(d) None of these

Question. The straight line x/a + y/b = 2 touches the curve (x/a)n + (y/b)n = 2 at the point (a, b) for
(a) n = 1, 2
(b) n = 3, 4, –5
(c) n = 1, 2, 3
(d) any value of n

Question. Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
(a) 2a/3
(b) 2a/√3
(c) a/3
(d) a/5

Question. A right circular cylinder which is open at the top and has a given surface area, will have the greatest volume if its height h and radius r are related by
(a) 2h = r
(b) h = 4r
(c) h = 2r
(d) h = r

Case Based Questions

Megha wants to prepare ahandmade gift box for her friend’s birthday at home. For making lower part of box, she takes a square piece of cardboard of side 20 cm. 
Based on the above information, answer the following questions

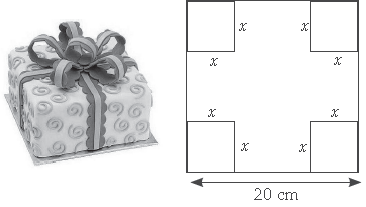
Question. Volume of the open box formed by folding up the cutting corner can be expressed as
(a) V = x(20 – 2x)²
(b) V = x/2(20 + x)(20 + x)
(c) V = x/3(20 – 2x) (20 + 2x)
(d) V = x(20 – 2x)(20 – x)

Question. If x cm be the length of each side of the square cardboard which is to be cut off from corners of the square piece of side 20 cm, then possible value of x will be given by the interval
(a) [0, 20]
(b) [0, 10]
(c) [0, 3]
(d) None of these

Question. Megha is interested in maximising the volume of the box. So, what should be the side of the square to be cut off so that the volume of the box is maximum?
(a) 12 cm
(b) 8 cm
(c) (10/3) cm
(d) 2 cm

Question. The values of x for which dV/dx = 0, are

Question. The maximum value of the volume is

Shobhit′s father wants to construct a rectangular garden using a brick will on one side of the garden and wire fencing for the other three sides as shown in figure. He has 200 ft. of wire fencing.

Based on the above information, answer the following questions:

Question. If x denotes the length of side of garden perpendicular to brick wall and y denotes the length of side parallel to brick wall, then find the relation representing total amount of fencing wire.
(a) x + 2y = 150
(b) x + 2y = 50
(c) y + 2x = 200
(d) y + 2x = 100

Question. To construct a garden using 200 ft. of fencing, we need to maximise its
(a) volume
(b) area
(c) perimeter
(d) length of the side

Question. Maximum value of A(x) occurs at x equals
(a) 50 ft.
(b) 30 ft.
(c) 26 ft.
(d) 31 ft.

Question. Area of the garden as a function of x, say A(x), can be represented as
(a) 200 + 2x²
(b) x – 2x²
(c) 200x – 2x²
(d) 200 – x²

Question. Maximum area of garden will be
(a) 2500 sq. ft
(b) 4000 sq. ft
(c) 5000 sq. ft
(d) 6000 sq. ft

The government declare that farmers can get ₹300 per quintal for their onions on 1st July and after that the price will be dropped by ₹3 per quintal per extra day. Shyam’s father has 80 quintal of onions in the field on 1st July and he estimates that crop is increasing at the rate of 1 quintal per day.

Based on the given information, answer the following questions:

Question. Revenue R as a function of x can be represented as
(a) R(x) = 3x² – 60x – 24000
(b) R(x) = –3x² + 60x + 24000
(c) R(x) = 3x² + 40x + 16000
(d) R(x) = 3x² – 60x – 14000

Question. If x is the number of days after 1st July, then price and quantity of onion respectively can be expressed as
(a) ₹(300 – 3x), (80 + x) quintals
(b) ₹(300 – 3x), (80 – x) quintals
(c) ₹(300 + x), 80 quintals
(d) None of these

Question. On which day should Shyam’s father harvest the onions to maximise his revenue?
(a) 11^th July
(b) 20^th July
(c) 12^th July
(d) 22^nd July

Question. Find the number of days after 1^st July, when Shyam’s father attain maximum revenue.
(a) 10
(b) 20
(c) 12
(d) 22

Question. Maximum revenue is equal to
(a) ₹20,000
(b) ₹24,000
(c) ₹24,300
(d) ₹24,700

An owner of an electric bike rental company have determined that if they charge customers ₹x per day to rent a bike, where 50 ≤ x ≤ 200, then number of bikes (n), they rent per day can be shown by linear function n(x) = 2000 – 10x. If they charge ₹50 per day or less, they will rent all their bikes. If they charge ₹200 or more per day, they will not rent any bike.

Based on the above information, answer the following questions:

Question. If R(x) denote the revenue, then maximum value of R(x) occur when x equals
(a) 10
(b) 100
(c) 1000
(d) 50

Question. Total revenue R as a function of x can be represented as
(a) 2000x – 10x²
(b) 2000x + 10x²
(c) 2000 – 10x
(d) 2000 – 5x²

Question. The number of bikes rented per day, if x = 105 is
(a) 850
(b) 900
(c) 950
(d) 1000

Question. At x = 260, the revenue collected by the company is
(a) ₹10
(b) ₹500
(c) ₹0
(d) ₹1000

Question. Maximum revenue collected by company is
(a) ₹40,000
(b) ₹50,000
(c) ₹75,000
(d) ₹1,00,000

Mr. Sahil is the owner of a high rise residential society having 50 apartments. When he set rent at ₹10,000/month, all apartments are rented. If he increases rent by ₹250/ month, one fewer apartment is rented. The maintenance cost for each occupied units is ₹500 month.

Based on the above information answer the following questions:

Question. If x represents the number of apartments which are not rented, then the profit expressed as a function of x is
(a) (50 – x) (38 + x)
(b) (50 + x) (38 – x)
(c) 250(50 – x)(38 + x)
(d) 250(50 + x) (38 – x)

Question. If P is the rent price per apartment and N is the number of rented apartment, then profit is given by
(a) NP
(b) (N – 500)P
(c) N(P – 500)
(d) none of these

Question. If P = 11,000 then the profit is
(a) ₹4,83,000
(b) ₹5,00,000
(c) ₹5,05,000
(d) ₹6,50,000

Question. If P = 10,500 then N =
(a) 47
(b) 48
(c) 49
(d) 50

Question. The rent that maximises the total amount of profit is
(a) ₹11,000
(b) ₹11,500
(c) ₹15,800
(d) ₹16,500

The shape of a toy is given as f(x) = 6(2x⁴ – x²). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Question. Find the slope of the normal based on the position of the stick.
(a) 360
(b) –360
(c) 1/360
(d) −1/360

Question. Which value from the following may be abscissa of critical point?

Question. Find the second order derivative of the function at x = 5.
(a) 598
(b) 1,176
(c) 3,588
(d) 3312

Question. What will be the equation of the tangent at the critical point if it passes though (2, 3)?
(a) x + 360y = 1082
(b) y = 360x – 717
(c) x = 717y + 360
(d) none

Question. At which of the following intervals will f(x) be increasing?
(a) (–∞, –1/2) ∪ (1/2, ∞)
(b) (–1/2, 0) ∪ (1/2, ∞)
(c) (0, 1/2) ∪ (1/2, ∞)
(d) (–∞, –1/2) ∪ (0, ∞)

The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – (1/2)x² where x is the number of days exposed to sunlight.

Question. What is the number of days it will take for the plant to grow to the maximum height?
(a) 4
(b) 6
(c) 7
(b) 10

Question. The rate of growth of the plant with respect to sunlight is _

Question. What will be the height of the plant after 2 days?
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm

Question. What is the maximum height of the plant?
(a) 12 cm
(b) 10 cm
(c) 8 cm
(d) 6 cm

Question. If the height of the plant is 7/2 cm, the number of days it has been exposed to the sunlight is
(a) 2
(b) 3
(c) 4
(d) 1

P(x) = –5x² + 125x + 37500 is the total profit function of a company, where x is the production of the company

Question. What will be the maximum profit?
(a) ₹38,28,125
(b) ₹38,281.25
(c) ₹39,000
(d) None

Question. What will be the production when the profit is maximum?
(a) 37,500
(b) 12.5
(c) – 12.5
(d) – 37,500

Question. When the production is 2 units what will be the profit of the company?
(a) 37,500
(b) 37,730
(c) 37,770
(d) None

Question. Check in which interval the profit is strictly increasing.
(a) (12.5, ∞)
(b) for all real numbers
(c) for all positive real numbers
(d) (0, 12.5)

Question. What will be production of the company when the profit is ₹38,250?
(a) 15
(b) 30
(c) 2
(d) data is not sufficient to find