Please refer to Class 12 Mathematics Sample Paper Term 1 With Solutions Set A provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Term 1 Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
Term 1 Sample Paper for Class 12 Mathematics With Solutions Set A
SECTION-A
In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.
1. What is the principal value branch of cosec–1 x ?
(A) (–1, 1)
(B) [–1, 1]
(C) [-π/2 , π/2]- {0}
(D) [–π/2 , π/2]
Answer
C
2. Find the value of k if derivative of the function exists f(3) = 4, f(x) = kx3/3
(A) k =4/5
(B) k = 4/7
(C) k = 4/9
(D) k = 4/9
Answer
C
3. The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(A) 9
(B) 28
(C) 512
(D) 64
Answer
C
4. Calculate the determinant of the given matrix
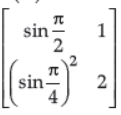
(A) 1/2
(B) -1/2
(C) 3/2
(D) None of the above
Answer
C
5. Which of the following is satisfied by the function, f (x)= 2 sin x−x+1 in the interval (0,π/2)
(A) Function has local minimum at x = π/3
(B) Function has local maximum at x = π/3
(C) Function has no critical points in the given interval
(D) Function is increasing in the given interval
Answer
B
6. If
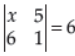
= then the value of x is:
(A) –6
(B) –36
(C) 6
(D) 36
Answer
D
7. If the set A contains 3 elements and the set B contains 6 elements, then the number of bijective mappings from A to B is:
(A) 520
(B) 10
(C) 0
(D) None of these
Answer
C
8. If A =
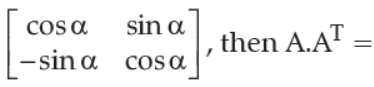
(A) Null Matrix
(B) I
(C) A
(D) –A
Answer
B
9. The normal to curve y = 7x2 – x4 at x=2 passes through
(A) (30,4)
(B) (20,4)
(C) (10,5)
(D) (5,20)
Answer
B
10. What is the domain of the sin–1 x ?
(A) [–∞, ∞]
(B) (–∞, ∞)
(C) (–1, 1)
(D) [–1, 1]
Answer
D
11. Let f : R → R be defined as f (x) = 5x. Choose the correct answer.
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
Answer
A
12. Find dy/dx where y = cosec x log x.
(A) y = – cosecx cot x logx + cosec x/x
(B) y = cosecx cot x logx + cosec x – cot x/x
(C) y = – cosecx cot x logx + cosec x – cot x/x
(D) y = cosecx cot x logx + cot x/x
Answer
A
13. The value of x for the given determinant
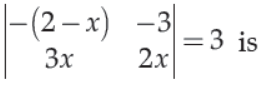
(A) ± 3
(B) 3,1/2
(C) 0
(D) – 3,1/2
Answer
D
14. What is second derivative of the function, y = log(√1-x2).
(A) -1-x2/(1-x2)2
(B) 1-x2/(1-x2)2
(C) -1+x2/(1-x2)2
(D) 1+x2/(1-x2)2
Answer
A
15. Skew symmetric matrix is also called:
(A) symmetric
(B) identical matrix
(C) square matrix
(D) anti symmetric
Answer
D
16. What are the local maximum and minimum for the function 3x4 −54x2 −108x+4x3 in the interval [–5 5]
(A) x =−1, 3,−3
(B) x =−1, 3,−2
(C) x =−1, 4,−4
(D) x = 2, 3,−3
Answer
A
17. Matrix A=
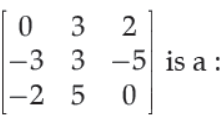
(A) Skew-symmetric matrix
(B) Symmetric matrix
(C) Scalar matrix
(D) None of these
Answer
D
18. Find dy/dx where y = e−sin -1 x
(A) -1/√1-x2
(B) -y/√1+x2
(C) -esin -1x/√1-x2
(D) -y/√1- x
Answer
A
19. For the constraints of a LPP problem given by x1 + 2x2 ≤ 2000, x1 + x2 ≤ 1500, x2 ≤ 600 and x1, x2 ≥ 0, the points does not lie in the positive bounded region.
(A) (1000,0)
(B) (0, 500)
(C) (2, 0)
(D) (2000,0)
Answer
D
20. If y = f (x)= sin(log x) ,then dy/dx =
(A) cos(log x)/x
(B) sin(log x)/x
(C) log x/x
(D) cos x/x
Answer
A
SECTION-B
In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.
21. Let T be the set of all triangles in a plane with R is a relation in T given by R = {(T1, T2) : T1 is congruent to T2}. Then R is
(A) Non commutative relation
(B) A universal relation
(C) An equivalence relation
(D) An empty relation
Answer
C
22. Consider the function 3x4 +20x3 −36x2 +44 in the interval [−5,10] , function is maximum at
(A) 1
(B) 0
(C) 2
(D) 3
Answer
B
23. The graph of x ≤ 2 and y ≥ 2 will be situated in quadrants.
(A) I only
(B) II only
(C) III only
(D) I and II
Answer
D
24. What is the value of l in the function
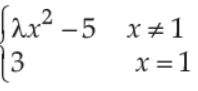
provided function is continuous at x = 1?
(A) 2
(B) 4
(C) 8
(D) 16
Answer
C
25. If A is a 3 × 3 matrix such that |A| = 8, then |3A| equals
(A) 8
(B) 24
(C) 72
(D) 216
Answer
D
26. The function f(x) = tan x – x
(A) always increases
(B) always decreases
(C) never increases
(D) sometimes increases and sometimes decreases
Answer
A
27. What is the domain of the cot–1 x ?
(A) [–∞, ∞]
(B) (–∞, ∞)
(C) (–∞, –1] ∪ [1, ∞)
(D) [–1,1]
Answer
B
28. If A is skew symmetric matrix of order 3, then the value of |A| is
(A) 3
(B) 0
(C) 9
(D) 27
Answer
B
29. The function f(x) = 4sin3x – 6 sin2 x + 12 sinx + 100 is strictly

Answer
B
30. If A = {1, 2}, B = {3,4, 5} and f = {(1, 3), (2, 5)} is a function from A to B, then f(x) is
(A) onto
(B) bijective
(C) one-one
(D) None of these
Answer
C
31. The function f(x) = e|x| is
(A) continuous everywhere but not differentiable at x = 0
(B) continuous and differentiable everywhere
(C) not continuous at x = 0
(D) none of these
Answer
A
32. The matrix
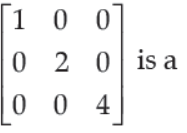
(A) identity matrix
(B) symmetric matrix
(C) skew-symmetric matrix
(D) None of these
Answer
B
33. Z = 7x + y, subject to 5x + y £ 5, x + y ³ 3, x ³ 0, y ≥ 0. Maximum value of Z occurs at
(A) (3, 0)
(B) (1/2 , 5/2)
(C) (7, 0)
(D) (0, 5)
Answer
C
34. Which of the following functions is decreasing on (0 , π/2) .
(A) sin 2x
(B) tan x
(C) cos x
(D) cos 3x
Answer
C
35. If A and B are symmetric matrices of same order, then AB – BA is a:
(A) Skew-symmetric matrix
(B) Symmetric matrix
(C) Zero matrix
(D) Identity matrix
Answer
A
36. The principal value of cos-1 (√3/2) is
(A) 3π/4
(B) π/4
(C) π/2
(D) π/6
Answer
D
37. The domain of sin–1 x is :
(A) [0, 1]
(B) [–1, ∞]
(C) (– ∞, ∞)
(D) [–1, 1]
Answer
D
38. If
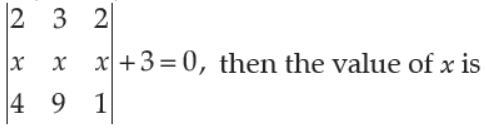
(A) 3
(B) 0
(C) – 1
(D) 1
Answer
C
39. The contentment obtained after eating x units of a new dish at a trial function is given by the function f(x) = x3 + 6x2 + 5x + 3. The marginal contentment when 3 units of dish are consumed is ____________.
(A) 60
(B) 68
(C) 24
(D) 48
Answer
B
40. The matrix
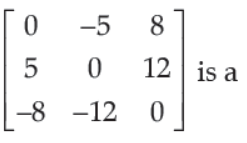
(A) diagonal matrix
(B) symmetric matrix
(C) skew symmetric matrix
(D) scalar matrix
Answer
C
SECTION-C
In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.
41. The optimal value of the objective function is attained at the points.
(A) X-axis only
(B) Y-axis only
(C) Corner points of feasible region
(D) Origin only
Answer
C
42. For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then at x = 3 the slope of curve is changing at ________ units/sec.
(A) –72
(B) –36
(C) 24
(D) 48
Answer
A
43. y = x(x – 3)2 decreases for the values of x given by :
(A) 1 < x < 3
(B) x < 0
(C) x > 0
(D) 0 < x < 3/2
Answer
A
44. For the constraints of linear optimizing function Z = x1 + x2 given by x1 + x2 ≤ 1, 3x1 + x2 ≥ 1, there is feasible region
(A) Yes
(B) No
(C) Can’t be determined
(D) None of these
Answer
B
45. Let A =
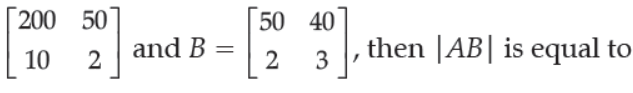
(A) 460
(B) 2000
(C) 3000
(D) – 7000
Answer
D
CASE-STUDY
A manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below
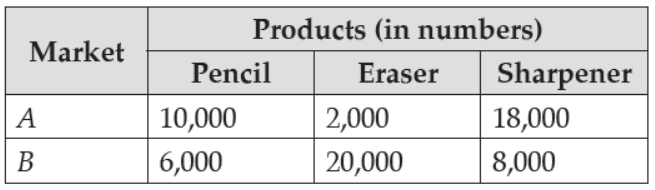

If the unit Sale price of Pencil, Eraser and Sharpener are ₹ 2.50, ₹ 1.50 and `₹ 1.00 respectively, and unit cost of the above three commodities are ₹ 2.00, ₹ 1.00 and ₹ 0.50 respectively, then, Based on the given information, answer the following questions.
46. Total revenue of market A
(A) ₹ 64,000
(B) ₹ 60,400
(C) ₹ 46,000
(D) ₹ 40600
Answer
C
47. Total revenue of market B
(A) ₹ 35,000
(B) ₹ 53,000
(C) ₹ 50,300
(D) ₹ 30,500
Answer
B
48. Cost incurred in market A
(A) ₹ 13,000
(B) ₹ 30,100
(C) ₹ 10,300
(D) ₹ 31,000
Answer
D
49. Profits in market A and B respectively are
(A) (₹ 15,000, ₹ 17,000)
(B) (₹ 17,000, ₹ 15,000)
(C) (₹ 51,000, ₹ 71,000)
(D) (₹ 10,000, ₹ 20,000)
Answer
A
50. Gross profit in both markets
(A) ₹ 23,000
(B) ₹ 20,300
(C) ₹ 32,000
(D) ₹ 30,200
Answer
C
