Check the below NCERT MCQ Class 12 Mathematics Chapter 9 Differential Equations with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Differential Equations Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Differential Equations Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 9 Differential Equations with solutions. Solve questions and compare with the answers provided below
Question. The degree of the differential equation (d3y/dx3)4 + (d2y/dx2)5 + dy/dx + y = 0 is
(a) 2
(b) 4
(c) 6
(d) 8
Answer
B
Question. Differential equation of all straight lines which are at a constant distance from the origin is
(a) (y + xy1)2 = p2(1+y12)
(b) (y – xy1)2 = p2(1-y12)
(c) (y – xy1)2 = p2(1+y12)
(d) None of these
Answer
C
Question. The orthogonal trajectories of the family of curve an-1 y=xn are given by (a is the arbitrary constant)
(a) xn +n2y = constant
(b) ny2 + x2 = constanat
(c) n2x+yn = constant
(d) n2x- yn = constant
Answer
B
Question. The degree of the differential equation satisfying the relation
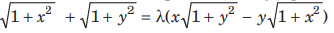
is
(a) 1
(b) 2
(c) 3
(d) None of these
Answer
A
Question. A tangent to the curve y=f (x) cuts the line y = x at a point which is at a distance of 1 unit from y-axis. The equation of the curve is
(a) x-1/y-1=C
(b) x/y= C
(c) xy = C
(d) None of these
Answer
A
Question. A curve passes through the point (0,1) and the gradient at(x ,y )on it is y( xy-1). The equation of the curve is
(a) y(x-1)=1
(b) y(x+1)=1
(c)x(y+1)=1
(d) x(y-1)=1
Answer
B
Question. The integrating factor of the differentiable equation (xy-1)dy/dx+y2=0 is
(a) 1/x
(b) 1/y
(c) 1/xy
(d) xy
Answer
B
Question. The equation of a curve passing through (2,7/2) and having gradient 1-1/x2 at (x,y) is
(a) y =x2+x+1
(b) xy =x2+x+1
(c) xy=x+1
(d) None of these
Answer
B
Question. A function y =f (x) has a second order derivative f ‘(x)=6(x-1). If is its graph passes through the point (2,1) and at the point the tangent to the graph is y= 3x-5, then the function
(a) (x+1)3
(b) (x-1)3
(c) (x+1)3
(d) (x-1)2
Answer
B
Question. An inverted conical tank of 2 m radius and 4 m height is initially full of water has an outlet at bottom. The outlet is opened at some instant. The rate of flow through the outlet at any time t is 6 h 3/2,where h is height of water level above the outlet at time t.Then, the time it takes to empty the tank, is
(a) 2π/9unit
(b) π/9 unit
(c) 2π/8unit
(d) None of these
Answer
A
Question. The solution of the differential equation
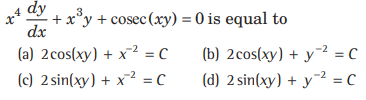
Answer
A
Question. The solution of the differential equation
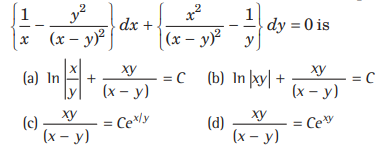
Answer
A
Question. The differential equation of the family of curves for which the length of the normal is equal to a constant k, is given by
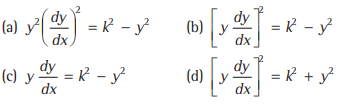
Answer
B
Question. The equation of the curve for which the square of the ordinate is twice the rectangle contained by the abscissa and the intercept of the normal on x-axis and passing through (2,1) is
(a) x2+y2-x=0
(b) 4x2+ 2y2-9y=0
(c) 2x2+4y2-9x=0
(d) 4x2+2y2-9x=0
Answer
D
Question. A curve y = f(x) passes through the point P(1,1) The normal to the curve at point P is a (y-1) + (x-1)=0. If the slope of the tangent at any point on the curve is proportional to the ordinate at that point, then the equation of the curve is
(a)y=eax-1
(b) y=eax+1
(c)y=eax+a
(d) y=ea(x-1)
Answer
D
Question. The differential equation representing all lines at a distance p from the origin is
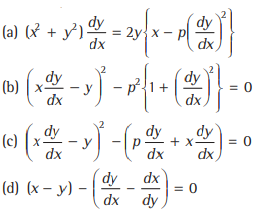
Answer
B
Question. The equation of the curve in which the portion of y-axis cut off between the origin and the tangent varies as the cube of the abscissa of the point of contact is
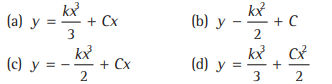
Answer
C
Question. A tangent and a normal to curve at any point P meet the x and y axes at A, B and C, D, respectively. If the centre of circle through O,C, P and B lies on the line y =x (O is the origin), then the differential equation of all such curves is
(a) dy/dx = y-x/y+x
(b) dy/dx=y2-x2/y2+x2
(c) dy/dx=x-y/xy
(d) dy/dx = xy/y+x
Answer
A
Question. Let y f x = (x) be a curve passing through (e ,ee), which satisfy the differential equation
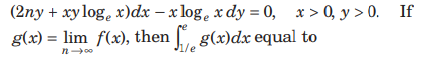
(a) e
(b) 1
(c) 0
(d) 2
Answer
C
Question. Solution of the differential equation
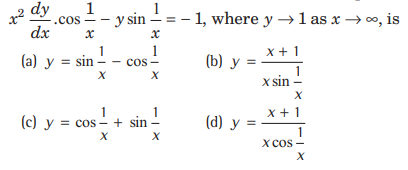
Answer
A
Question. A particle of mass m is moving in straight line is acted on by an attrctive force mk2 a2/x2 for x ≥ a and 2mk2x/a for x<a. If the particle starts from rest at the point x= 2a then it will reach the point x = 0 with a speed
(a) k√a
(b)k√2a
(c) k√a3
(d) 1/k√a
Answer
C
Question.
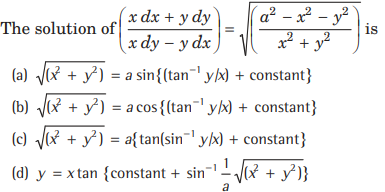
Answer
(A,B)
Question. A curve is such that the portion of the x-axis cut off between the origin and tangent at a point is twice the abscissa and which passes through the point (1,2) The equation of the curve is
(a) xy = 1
(b) xy = 2
(c) xy = 3
(d) xy = 0
Answer
B
Question.
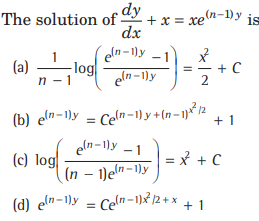
Answer
(A,B)
Question.
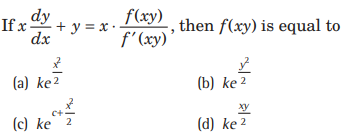
Answer
(A,C)
Question. The solution of the differential equation
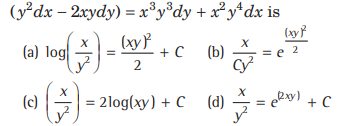
Answer
(A,B)
Question.
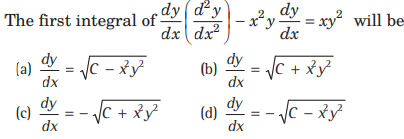
Answer
(B,C)
Directions (Q. Nos. 26-29) Let y f x = ( ) and y g x = ( ) be the pair of curves such that(i) the tangents at point with equal abscissae intersect on y-axis.
(ii) the normal drawn at points with equal abscissae intersect on x-axis and
(iii) one curve passes through (1, 1) and the other one passes through (2, 3), then
Question. The curve g (x) is given by
(a) x-1/x
(b) x+2/x
(c) x2-1/x2
(d) x2+1/x2
Answer
B
Question. The number of positive integral solutions for f (x) =g(x), are
(a) 4
(b) 5
(c) 6
(d) None of these
Answer
D
Question. The curve f x) is given by
(a) 2/x-x
(b) 2x2-1/x
(c) 2/2×2-x
(d) 2/x-x2
Answer
A
Question. The value of
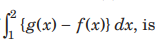
(a) 2
(b) 3
(c) 4
(d) 5
Answer
B
Question. Solution of differential equation (x2 – 2x + 2y2) dx + 2xy dy = 0 is
(a) y2 = 2x – 1/4 x2 + c/x2
(b) y2 = 2/3 x – x2 + c/x2
(c) y2 = 2/3 x – x2/4 + c/x2
(d) None of these
Answer
C
Question. The solution of x3 dy/dx + 4x2 tan y = ex sec y satisfying y (1) = 0 is :
(a) tan y = (x – 2) ex log x
(b) sin y = ex (x -1)x-4
(c) tan y=(x -1)exx-3
(d) sin y = ex (x -1) x-3
Answer
B
Question. The order and degree of the differential equation d2y/dx2 + (dy/dx)1/4 + x1/5 = 0 , respectively, are
(a) 2 and not defined
(b) 2 and 2
(c) 2 and 3
(d) 3 and 3
Answer
A
Question. tan–1 x + tan–1 y = c is the general solution of the differential equation
(a) dy/dx = 1+y2/1+x2
(b) dy/dx = 1 + x2/1+y2
(c) (1 + x2) dy + (1 + y2) dx = 0
(d) (1 + x2) dx + (1 + y2) dy = 0
Answer
C
Question. The differential equation obtained by eliminating the arbitrary constants a and b from xy = aex + be–x is
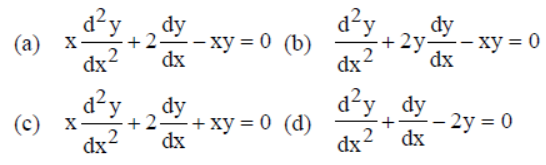
Answer
A
Question. To solve first order linear differential equation, we use following steps
I. Write the solution of the given differential equation as y (IF) = ∫(Qx IF)dx + C
II. Write the given differential equation in the from dy/dx + Py = Q , where P and Q are constants or functions of x only.
III. Find the integrating factor (IF) e∫ P dx The correct order of the above steps is
(a) II, III, I
(b) II, I, III
(c) III, I, II
(d) I, III, II
Answer
A
Question. The order of the differential equation whose solution is :
y = a cos x + b sin x + ce–x is :
(a) 3
(b) 2
(c) 1
(d) None of these
Answer
A
Question. The elimination of constants A, B and C from y = A + Bx – Ce–x leads the differential equation:
(a) y” + y”‘ = 0
(b) y” – y”‘ = 0
(c) y’ + ex = 0
(d) y” + ex = 0
Answer
A
Question. Which of the following equation has y = c1 ex + c2 e–x as the general solution?
(a) d2y/dx2 + y = 0
(b) d2y/dx2 – y = 0
(c) d2y/dx2 + 1 = 0
(d) d2y/dx2 – 1 = 0
Answer
B
Question. The order and degree of the differential equation whose solution is y = cx +c2 – 3c3/2 + 2 , where c is a parameter, is
(a) order = 4, degree = 4
(b) order = 4, degree = 1
(c) order = 1, degree = 4
(d) None of these
Answer
C
Question. A first order-first degree differential equation is of the form
(a) d2y/dx2 = F (x, y)
(b) d3y/dx2 = F (x, y)
(c) (dy/dx)2 = F (x, y)
(d) dy/dx = F (x, y)
Answer
D
Question. A steam boat is moving at velocity V when steam is shut off.
Given that the retardation at any subsequent time is equal to the magnitude of the velocity at that time. The velocity v in time t after steam is shut off is
(a) v = Vt
(b) v = Vt – V
(c) v = Vet
(d) v = Ve–t
Answer
D
Question. A family of curves is given by the equation x2/a2 + y2/b2 = 1 . The differential equation representing this family of curves is given by xy d2y/dx2 + Ax (dy/dx)2 – y dy/dx = 0 .
The value of A is
(a) 0
(b) 1
(c) 3
(d) 5
Answer
B
Question. The solution of the differential equation y’= y/x + φ(y/x)/φ'(y/x) is
(a) x φ (y/x) = k
(b) φ (y/x) = kx
(c) y φ (y/x) = k
(d) φ (y/x) = ky
Answer
B
Question. The equation of a curve whose tangent at any point on it different from origin has slope y + y/x , is
(a) y = ex
(b) y = kx. ex
(c) y = kx
(d) y = k. ex2
Answer
B
Question. The solution of the differential equation (1+ex/y) dx + ex/y (1+x/y) dy = 0
(a) yex + x = C
(b) xey + y = C
(c) yey/x + y = C
(d) yex/y + y = C
Answer
D
Question. The solution of the differential equation ydx – xdy + 3x2 y2 ex3 dx = 0
(a) x/y + ex3 = c
(b) x/y – ex3 = c
(c) y/x + ex3 = c
(d) y/x – ex3 = c
Answer
A
Question. The differential equation of the form dy/dx + Py = Q
where, P and Q are constants or functions of x only, is known as a
(a) first order differential equation
(b) linear differential equation
(c) first order linear differential equation
(d) None of the above
Answer
C
Question. Which of the following is/are first order linear differential equation?
(a) dy/dx + y = sin x
(b) dy/dx + (1/x) y = ex
(c) dy/dx + (y/x log x) = 1/x
(d) All the above
Answer
D
Question. If p and q are the order and degree of the differential equation y dy/dx + x3 d2y/dx2 + xy = cos x, then
(a) p < q
(b) p = q
(c) p > q
(d) None of these
Answer
C
Question. The differential equation obtained by eliminating arbitrary constants from y = aebx is
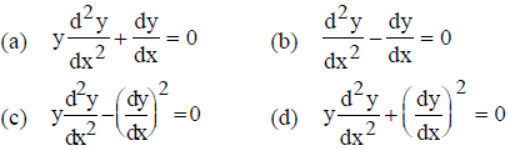
Answer
C
Question. The degree of the differential equation y32/3 + 2 + 3y2 + y1 = 0 is :
(a) 1
(b) 2
(c) 3
(d) None of these
Answer
B
Question. For the differential equation d2y/dx2 + y = 0 , if there is a function y = φ (x) that will satisfy it, then the function y = φ (x) is called
(a) solution curve only
(b) integral curve only
(c) solution curve or integral curve
(d) None of the above
Answer
C
Question.
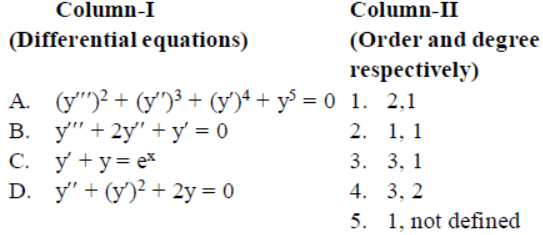
Codes
A B C D
(a) 5 4 1 3
(b) 2 4 1 3
(c) 4 2 3 1
(d) 4 3 2 1
Answer
D
Question. The degree of the equation ex d2y/dx2 + sin (dy/dx) = 3 is
(a) 2
(b) 0
(c) not defined
(d) 1
Answer
C
Question. The equation of the curve satisfying the differential equation y2 (x2 + 1) = 2 xy, passing through the point (0, 1) and having slope of tangent at x = 0 as 3, is
(a) y = x3 + 3x + 1
(b) y = x2 + 3x + 1
(c) y = x3 + 3x
(d) y = x3 + 1
Answer
A
Question. The degree of the differential equation satisfied by the curve √1+ x – a √1+ y = 1, is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
Question. The female-male ratio of a village decreases continuously at the rate proportional to their ratio at any time. If the ratio of female : male of the villages was 980 : 1000 in 2001 and 920 : 1000 in 2011. What will be the ratio in 2021 ?
(a) 864 : 1000
(b) 864 : 100
(c) 1000 : 864
(d) 100 : 864
Answer
A
Question. An equation which involves variables as well as derivative of the dependent variable with respect to independent variable, is known as
(a) differential equation
(b) integral equation
(c) linear equation
(d) quadratic equation
Answer
A
Question. If y = (x+√1+x2)n , then (1 + x2) d2y/dx2 + x dy/dx is
(a) n2y
(b) –n2y
(c) 0 – y
(d) 2x2y
Answer
A
Question. For y = cos kx to be a solution of differential equation d2y/dx2 + 4y = 0, the value of k is
(a) 2
(b) 4
(c) 6
(d) 8
Answer
A
Question. The integrating factor of the differential equation x dy/dx – y = 2x2 is
(a) e–x
(b) e–y
(c) 1/x
(d) x
Answer
C
Question. In a bank, principal increases continuously at the rate of 5% per year. In how many years ₹ 1000 double itself?
(a) 2
(b) 20
(c) 20 loge2
(d) 2 loge20
Answer
C
Question. The equation of curve through the point (1, 0), if the slope of the tangent to the curve at any point (x, y) is y-1/x2+x , is
(a) (y + 1) (x – 1) + 2x = 0
(b) (y + 1) (x – 1) – 2x = 0
(c) (y – 1) (x – 1) + 2x = 0
(d) (y – 1) (x + 1) + 2x = 0
Answer
D
Question. The general solution of the homogeneous differential equation of the type.
dy/dx = F(x, y) = g (y/x) , when y = v : x is
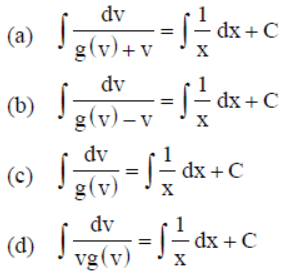
Answer
B
Question. In order to solve the differential equation x cos x dy/dx + y(xsin x cos x) = 1 the integrating factor is:
(a) x cos x
(b) x sec x
(c) x sin x
(d) x cosec x
Answer
B
Question. The diffrerential equation dy/dx + 1/x sin 2y = x3 cos2 y represents a family of curves given by the equation
(a) x6 + 6x2 = Ctan y
(b) 6x2 tan y = x6 + C
(c) sin 2y = x3 cos2 y + C
(d) none of these
Answer
B
Question.

Codes
A B C D E F
(a) 2 2 4 3 1 1
(b) 1 1 1 1 2 3
(c) 3 4 1 1 2 3
(d) 1 1 1 3 4 2
Answer
B
Assertion and Reason type Questions :
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion : dy/dx + x2y = 5 is a first order linear differential equation.
Reason: If P and Q are functions of x only or constant then differential equation of the form dy/dx + Py = Q is a first order linear differential equation.
Answer
A
Question. Assertion: Order of the differential equation whose solution is y = c1e x + c2 + c3e x + c4 is 4.
Reason: Order of the differential equation is equal to the number of independent arbitrary constant mentioned in the solution of differential equation.
Answer
D
Question. Assertion: The differential equation y3 dy + (x + y2) dx = 0 becomes homogeneous if we put y2 = t.
Reason: All differential equation of first order first degree becomes homogeneous if we put y = tx.
Answer
C
Question. Assertion: The differential equation of all circles in a plane must be of order 3.
Reason: If three points are non-collinear, then only one circle always passing through these points.
Answer
B
Question. Assertion : The differential equation dy/dx + x = cos y and dy/dx + -2x/y = y2 e-y are first order linear differential equations.
Reason : The differential equation of the form dy/dx + P1x = Q1 where, P1 and Q1 are constants or functions of y only, is called first order linear differential equation.
Answer
A


