Students can read the important questions given below for Mechanical Properties of Fluids Class 11 Physics. All Mechanical Properties of Fluids Class 11 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 11 Physics Important Questions provided for all chapters to get better marks in examinations. Physics Question Bank Class 11 is available on our website for free download in PDF.
Important Questions of Mechanical Properties of Fluids Class 11
Very Short Answer Type Questions :
Question. What is the effect of temperature on surface tension?
Answer : Surface tension decreases when temperature of the liquid increases because cohesive forces decrease with an increase of molecular thermal activity.
Question. It is painful to walk barefooted on the ground covered with edged pebbles. Why?
Answer : While walking, when entire weight of our body gets supported on the sharp edge of any pebble, it will exert a large pressure on our feet due to reaction. This causes consid-erable pain on our feet.
Question. When air is blown between two balls suspended close to each other they are attracted towards each other. Why?
Answer : When air is blown between the two balls, the velocity is increased and hence pressure is decreased (as per the Bernoulli’s principle). On the outer sides of the balls, the pressure is high and hence the two balls get attracted.
Question. What is reciprocal of viscosity known as?
Answer : Fluidity is the reciprocal of viscosity.
Question. What is the net weight of a body when it falls with terminal velocity through a viscous medium?
Answer : Zero, because when the body attains terminal velocity then the net force acting on the body is zero.
Question. Why does velocity increase when water flowing in a broad pipe enters a narrow pipe?
Answer : When water enters into a narrow pipe, the area of cross-section (A) decreases and consequently velocity (v) increases as Av = constant.
Question. The diameter of ball A is half of that of ball B. What will be the ratio of their terminal velocities in water if all the factors remain same?
Answer : As, terminal velocity, v ∝ r2 ∝ d2.
Therefore, ratio of terminal velocities of balls A and B is

Question. Why two ships moving in parallel directions close to each other get attracted?
Answer : According to Bernoulli’s theorem for horizontal flow P + 1/2 pv2 = constant.
As speed of water between the ships is more than outside the pressure between them gets reduced and pressure outside is more so the excess pressure pushes the ships close to each
other therefore they get attracted.
Question. Two soap bubbles have radii in the ratio 2 : 3. Find the ratio of the work done in blowing these bubbles.
Answer : Given : rA : rB = 2 : 3
As work done in blowing a soap bubble is given by
W = T × 2 × 4π2
where T is surface tension of the soap solution.
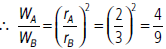
Question. Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
Answer : No, it does not matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation, provided the atmospheric pressure at the two points where Bernoulli’s equation is applied are significantly different.
Short Answer Type Questions :
Question. Explain, why a fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel?
Answer : When a fluid is flowing out of a small hole in a vessel, it acquires a large velocity and hence possesses large momentum. Since no external force is acting on the system, a backward velocity must be attained by the vessel (according to the law of conservation of momentum). As a result of it, backward thrust is experienced by the vessel.
Question. A bubble having surface tension S and radius R is formed on a ring of radius b (b<<R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. Calculate the radius at which the bubble separates from the ring.
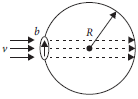
Answer : The bubble will separate from the ring when 2πb × 2σ sin θ = rAv2
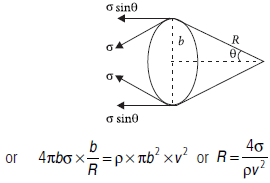
Question. (a) The three vessels shown in the given figure are filled with water. The three vessels have same base area.
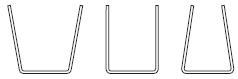
In which vessel, will the force on the base be minimum if,
(i) the vessels are filled to the same height.
(ii) the vessels are filled with equal volumes of water.
Give reason for your answer.
(b) An air bubble at the bottom of a lake rises to the sea level. What happens to its radius? Give reasons :
Answer :
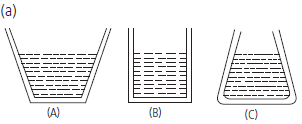
(i) Pressure depends upon the depth (h), nature of liquid (r) and acceleration due to gravity (g) while it is independent of the shape or cross-sectional area of the container. So, if the vessels of different shapes are filled to same height, the pressure at the base in each vessel will be the same
♦ PA = PB = PC
(ii) If the vessels are filled with equal volumes of water, each vessel may attain different height (h) of water due to different shapes of the vessels. The vessel with least height will have minimum pressure on its base . Therefore vessel A will have minimum pressure.
(b) The fluids moves from higher pressure to lower pressure and fluid pressure increases with depth. Hence, pressure at the top is less than that at the bottom so the air bubble will rise from bottom to sea level. When bubble moves from bottom to top, pressure decreases and in accordance with Boyle’s law volume V will increase i.e., the radius of the bubble increases.
Question. (a) What is the largest average velocity of blood flow in an artery of radius 2 × 10–3 m if the flow must remain laminar?
(b) What is the corresponding flow rate? (Take viscosity of blood to be 2.084 × 10–3 Pa s and density of blood is 1.06 × 103 kg/m3).
Answer :
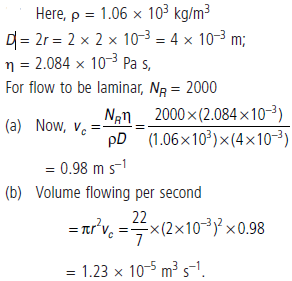
Question. Explain why, when we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers?
Answer : This can be explained from the equation of continuity i.e. a1v1 = a2v2. As we try to close a water tap with our fingers, the area of cross-section of the outlet of water jet is reduced considerably as the openings between our fingers provide constriction (i.e., regions of smaller area).
Thus velocity of water increases greatly and fast jets of water come through the openings between our fingers.
Question. An air bubble of diameter 2 mm rises steadily through a solution of density 1750 kg m–3 at the rate of 0.35 cm s–1. Calculate the coefficient of viscosity of the solution. The density of air is negligible.
Answer : The force of buoyancy B is equal to the weight of the displaced liquid. Thus, B = 4/3 πr3 σg
This force is upward. The viscous force acting downward is F = 6πηrv.
The weight of the air bubble may be neglected as the density of air is small. For uniform velocity, F = B
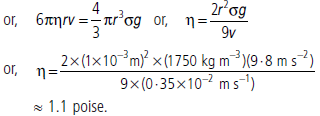
Question. The excess pressure inside a soap bubble is thrice the excess pressure inside a second soap bubble. What is the ratio between the volume of the first and the second bubble?
Answer : Given : P1 = 3P2
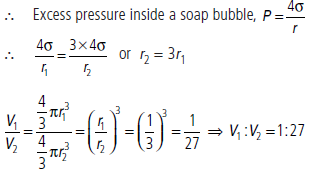
Question. In streamline flow, water entering a pipe having diameter of 2 cm and the speed of water is 1.0 m s–1. Eventually, the pipe tapers to a diameter of 1 cm. Calculate the speed of water where diameter of pipe is 1 cm.
Answer :
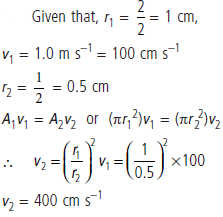
Question. A frame made of metallic wire enclosing a surface area A is covered with a soap film. If the area of the frame of metallic wire is reduced by 50%. What will be the change in the energy of the soap film?
Answer : Surface energy = surface tension × surface area,
E = S × 2A (… Soap film has two surfaces)
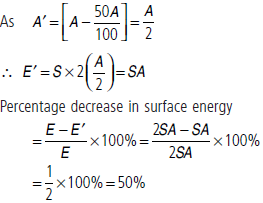
Question. Why the passengers are advised to remove the ink from their pens while going up in an aeroplane?
Answer : We know that atmospheric pressure decreases with height. Since ink inside the pen is filled at the atmospheric pressure existing on the surface of earth, it tends to come out to equalise the pressure. This can spoil the clothes of the passengers, so they are advised to remove the ink from the pen.
Question. A Venturimeter introduces a constriction of cross-sectional area A2 in a pipe of crosssectional area A1. The meter records the difference in pressure, P1–P2, between the ordinary fluid pressure, P1 and the pressure at the constriction, P2. From this, find the fluid speed in the unconstricted pipe.
Answer :
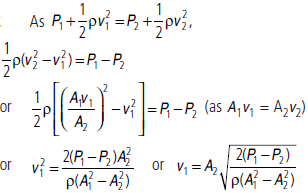
Question. What is the importance of Reynold’s number?
Answer : (i) If Reynold’s number Re lies between 0 and 2000, the liquid flow is streamlined or laminar.
(ii) If Re > 3000, the liquid flow is turbulent.
(iii) If 2000 < Re < 3000, the flow is unstable.
Question. A 50 kg girl wearing high heel shoes balanceson on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer :
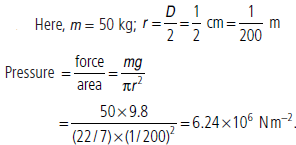
Question. The drop of liquid of density r is floating with 1/4 th inside the liquid A of density p1 and remaining in the liquid B of density p2. Then, find the relation between the densities of liquid A and B.
Answer :

Question. Why two streamlines cannot intersect each other?
Answer : The tangent to a streamline at any point gives the direction of flow of a liquid at that point. If two streamlines cross each other at a point, then two tangents can be drawn on that point, one to each streamline. This means that at that point, the liquid has two velocities of flow which is not possible in a streamline flow of a liquid. Hence, two streamlines cannot cross each other.
Question. On what principle working of hydraulic brakes are based? State that principle.
Answer : Hydraulic brakes are based on the principle of Pascal’s law. It states that if gravity effect is neglected, the pressure in a fluid at rest is same at all points.
Question. A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer : Here, depth of water column,
h = 3 km = 3 × 103 m
density of water, r = 103 kg m–3
If P be the pressure exerted by this water column at this depth, then
P = hrg = 3 × 103 × 103 × 9.8
= 29.4 × 106 Pa = 30 × 106 Pa = 3 × 107 Pa
As the structure is put on the sea, sea water will exert upward thrust of 3 × 107 Pa.
Maximum stress which the vertical off-shore structure can withstand = 109 Pa. (Given)
Then 3 × 107 Pa < 109 Pa
Thus we conclude that the structure is suitable as the stress applied by it is much lesser than the maximum stress it can withstand.
Question. A vessel having area of cross-section A contains a liquid upto a height h. At the bottom of the vessel, there is a small hole having area of cross-section a. Then what is the time taken for the liquid level to fall from height H1 to H2?
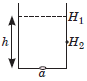
Answer : The velocity of efflux from the hole, v = √2gh Using equation of continuity, A1v1 = A2v2
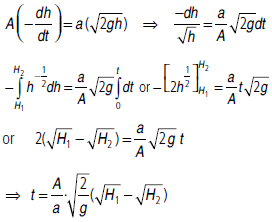
Question. Show that the Reynold’s number represents the ratio of the inertial force per unit area to the viscous force per unit area.
Answer : Consider a narrow tube having a cross-sectional area A. Suppose a fluid flows through it with a velocity v for a time interval Δt.
Length of the fluid = Velocity × time = v Δt
Volume of the fluid flowing through the tube in time Δt = Av Δt
Mass of the fluid,
Δm = Volume × density = Av Δt × r
Inertial force acting per unit area of the fluid
Question. Show that the Reynold’s number represents the ratio of the inertial force per unit area to the viscous force per unit area.
Answer : Consider a narrow tube having a cross-sectional area A. Suppose a fluid flows through it with a velocity v for a time interval Δt.
Length of the fluid = Velocity × time = v Δt
Volume of the fluid flowing through the tube in time Δt = Av Δt
Mass of the fluid,
Δm = Volume × density = Av Δt × r
Inertial force acting per unit area of the fluid
Question. Show that the Reynold’s number represents the ratio of the inertial force per unit area to the viscous force per unit area.
Answer : Consider a narrow tube having a cross-sectional area A. Suppose a fluid flows through it with a velocity v for a time interval Δt.
Length of the fluid = Velocity × time = v Δt
Volume of the fluid flowing through the tube in time Δt = Av Δt
Mass of the fluid,
Δm = Volume × density = Av Δt × r
Inertial force acting per unit area of the fluid

Thus Reynold’s number represents the ratio of the inertial force per unit area to the viscous force per unit area.
Question. Water from a tap emerges vertically downwards with an initial velocity v0. Assume pressure is constant throughout the stream of water and the flow is steady, find the distance from the tap at which cross-sectional area of stream is half of the cross-sectional area of stream at the tap.
Answer :
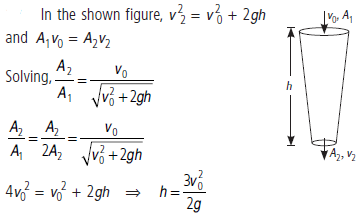
Question. The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 N m–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Answer :
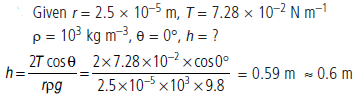
Which is the maximum height of rise of water in capillary action.
Many trees have heights much greater than 0.6 m so only this action is not sufficient for supply of water to the top of such long tree.
Question. Derive an expression for the pressure difference across the soap bubble.
Answer :
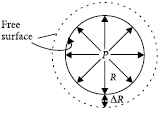
Excess pressure inside a soap bubble : Let us consider a liquid bubble (say a soap bubble) of radius R and let S be the surface tension of the liquid. We know that there is an excess pressure (P) inside the bubble and it acts normally outwards. Let the excess pressure increase the radius of the bubble from R to (R + ΔR) as shown.
Work done by the excess pressure, i.e.,
W = force × distance
= excess pressure × surface area × distance
= P × 4πR2 × ΔR
i.e., W = 4πPR2 × ΔR …(i)
The soap bubble has two free surfaces, one inside the bubble the other outside it.
Total increase in the surface area of the bubble, i.e.,
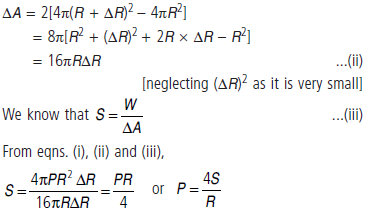
Since the excess pressure is inversely proportional to the radius of the bubble, it means smaller the bubble, greater the excess pressure inside it.
Question. A vessel filled with water is kept on a weighing pan and the scale adjusted to zero. A block of mass M and density ρ is suspended by a massless spring of spring constant k. This block is submerged inside the water in the vessel. What is the reading of the scale?
Answer : Let x be the compression on the spring.
As the block is in equilibrium
Mg – (kx + ρWVg) = 0
where ρW is the density of water and V is the volume of the block. The reading in the pan is the force applied by the water on the pan i.e.,
mvessel + mwater + ρwVg.
Since the scale has been adjusted to zero without the block, the new reading is ρwVg.

Long Answer Type Questions :
Question. Derive the ascent formula for rise of liquid in capillary tube. What will happen, if the length of the capillary tube is smaller than the height to which the liquid rises. Explain.
Answer : Ascent formula : Consider a capillary tube of radius r dipped in a liquid of surface tension T and density p. Suppose the liquid wets the sides of the tube. Then its meniscus will be concave. The shape of the meniscus of water will be nearly spherical if the capillary tube is of sufficiently narrow bore.
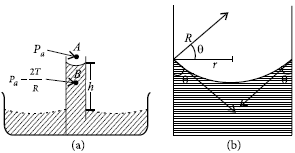
As the pressure is greater on the concave side of a liquid surface, so excess of pressure at a point A just above the meniscus compared to point B just below the meniscus is P = 2T/R, where R = radius of curvature of the concave meniscus. If θ is the angle of contact, then from the right angled triangle shown in figure (b), we have
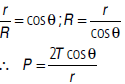
Due to this excess pressure P, the liquid rises in the capillary tube to height h when the hydrostatic pressure exerted by the liquid column becomes equal to the excess pressure P. Therefore, at equilibrium we have
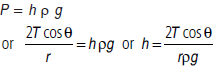
This is the ascent formula for the rise of liquid in a capillary tube. If we take into account the volume of the liquid
contained in the meniscus, then the above formula gets modified as
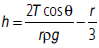
However, the factor r/3 can be neglected for a narrow tube.
(i) inversely proportional to the radius of the tube.
(ii) inversely proportional to the density of the liquid
(iii) directly proportional to the surface tension of the liquid.
Hence a liquid rises more in a narrower tube than in wider tube.
Rise of liquid in a tube of insufficient height: The height to which a liquid rises in a capillary tube is given by
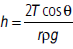
The radius r of the capillary tube and radius of curvature R of the liquid meniscus are related by r = R cos θ. Therefore
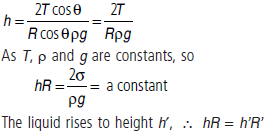
where R’ is the radius of curvature of the new meniscus at a height h’. As h’ < h, so R’ > R
Hence in a capillary tube of insufficient height, the liquid rises to the top and spreads out to a new radius of curvature R’ given by, R′ = hR/h′
But the liquid will not overflow.
Question. What is a tube of flow? Obtain a relation between the area of cross-section and the velocity of liquid at any point in a tube of flow. What conclusion do you draw from it?
Answer : Tube of flow : A bundle of streamlines forming a tubular region is called a tube of flow.
Relation between the area of cross-section and the velocity is given by equation of continuity of flow of incompressible fluids.
Equation of continuity : av = constant
Derivation :Consider a non-viscous and incompressible liquid flowing steadily between the sections A and B of a pipe of varying cross-section. Let a1 be the area of cross-section, v1 fluid velocity, p1 fluid density at section A; and the values of corresponding quantities at section B be a2, v2 and p2.
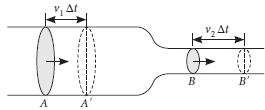
As m = volume × density = Area of cross-section × length × density
♦ Mass of fluid that flows through section A in time Δt, m1 = a1v1 Δtp1
Mass of fluid that flows through section B in time Δt, m2 = a2v2 Δtp2
By conservation of mass, m1 = m2
or a1v1 Δtp1 = a2v2 Δtp2
As the fluid is incompressible, so p1 = p2, and hence a1v1 = a2v2 or av = constant.
This is the equation of continuity.
Conclusion:
(i) When a fluid is in motion, it must move in such a wayvthat mass is conserved
(ii) For a steady flow through a control volume with many inlets and outlets, the net mass flow must be zero.
(iii) The liquid velocity at any section of the pipe is inversely proportional to the area of cross-section of the pipe at that section.
(iv) Velocity of flow decreases when the area of cross-section increases and vice versa.
Question. (a) Show that the pressure exerted by a liquid column is proportional to its height.
(b) State Pascal’s law.
Answer : (a) Consider a vessel of height h and cross-sectional area A filled with a liquid of density p. The weight of the liquid column exerts a downward thrust on the bottom of the vessel and the liquid exerts pressure. Weight of liquid column,
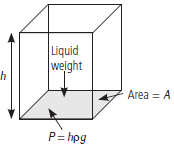
W = Mass of liquid × g = Volume × density × g
= Ah × r × g = Ahrg
Pressure exerted by the liquid column on the bottom of the vessel is

Thus, the pressure exerted by a liquid column at rest is proportional to (i) height of the liquid column and (ii) density of the liquid.
(b) Pascal’s law : If gravity effect is neglected, the pressure in a fluid at rest is same at all points.
Question. Explain how a small spherical rigid body attains terminal velocity while falling through a viscous liquid. Hence derive an expression for the terminal speed.
Answer : Terminal velocity : It is the maximum constant velocity acquired by the drop while falling in a viscous medium.
Expression for terminal velocity : Consider a spherical body of radius r falling through a viscous liquid of density s and coefficient of viscosity h. Let r be the density of the body. As the body falls, the various forces acting on the body are as shown in figure. These are

Clearly, the force of viscosity increases as the velocity of the body increases. A stage is reached, when the weight of the body becomes just equal to the sum of the upthrust and the viscous force. Then the body begins to fall with a constant maximum velocity, called terminal velocity.
When the body attains terminal velocity v, U + F = W
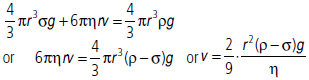
Thus, the value of terminal velocity v depends upon r, p, σ and η.


