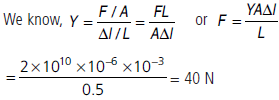Students can read the important questions given below for Mechanical Properties of Solids Class 11 Physics. All Mechanical Properties of Solids Class 11 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 11 Physics Important Questions provided for all chapters to get better marks in examinations. Physics Question Bank Class 11 is available on our website for free download in PDF.
Important Questions of Mechanical Properties of Solids Class 11
Very Short Answer Type Questions :
Question. Arrange the value of bulk modulus of elasticity of solids, liquids and gases according to their magnitude. Give reason.
Answer : Under constant stress, magnitude of bulk modulus of elasticity of material is inversely proportional to volumetric strain.
B ∝ 1 / Δ V/V
Since, gases has higher compressibility than liquid and solids have the least, therefore Bs > Bl > Bg.
Question. What is elastic fatigue?
Answer : The property of an elastic body by virtue of which its behaviour becomes less elastic under the action of repeated alternating deforming force is called elastic fatigue.
Question. Give the relation between bulk modulus and compressibility.
Answer : Compressibility is the reciprocal of bulk modulus.
k = 1/B
Question. What is the value of bulk modulus for an incompressible liquid?
Answer : Infinity.
Question. What does the slope of stress versus strain graph give?
Answer : The slope of stress-strain graph gives modulus of elasticity.
Question. Stress and pressure are both force per unit area. Then in what respect does stress differ from pressure?
Answer : Pressure is the external force per unit area, while stress is the internal restoring force which comes into play in a deformed body acting transversely, per unit area of the body.
Question. What is the value of compressibility for an incompressible liquid ?
Answer : Zero.
Question. Write dimensional formula of Young’s modulus.
Answer : Dimensional formula of, [Y] = [ML–1T–1].
Question. The ratio stress/strain remains constant for small deformation. What will be the effect on this ratio when the deformation made is very large?
Answer : When the deforming force is applied beyond elastic limit, the strain produced is more than that has been observed within elastic limit. Due to which the ratio stress/strain will decrease.
Question. What do you mean by ‘permanent set’ in a body?
Answer : Permanent set is the amount by which a material is stressed beyond its yield point and if the load is removed the material does not come back to its original shape or size.
Short Answer Type Questions :
Question. Why does modulus of elasticity of most of the materials decrease with the increase of temperature?
Answer : As the temperature increases, the interatomic forces of attraction become weaker. For given stress, a larger strain or deformation is produced at a higher temperature. Hence the modulus of elasticity (stress/strain) decreases with the increase of temperature.
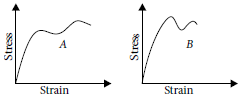
Question. The stress-strain graphs for materials A and B are shown in figure.
The graphs are drawn to the same scale.
(a) Which is more brittle?
(b) Which of the two is the stronger material?
Answer : (a) Material B is more brittle than A, because its plastic range of extension is very small.
(b) Material A is the stronger of the two materials. It is because, it can bear greater stress before the wire of this material breaks.
Question. Define the term stress. Give its units and dimensions. Describe the different types of stress.
Answer : When a body is subjected to a deforming force the restoring force developed per unit area is known as stress.
The magnitude of stress, S = F/A .
Its SI unit is N m2 and dimension is [ML–1 T1]. Different types of stress are
Longitudinal stress : The restoring force acting per unit area along the length of the body is called longitudinal stress.
Tensile stress : When a cylinder is stretched by two equal forces applied normal to its cross-sectional area, the restoring force per unit area developed in this case is called tensile stress.
Compressive stress : When a cylinder compressed under the action of deforming force, the restoring force per unit area is called compressive stress.
Question. A structural steel rod has a radius of 10 mm and a length of 1 m. A 100 kN force F stretches it along its length. Calculate (a) the stress, (b) elongation, and (c) strain on the rod. Given that the Young’s modulus of the structural steel is 2.0 × 1011 N m–2.
Answer : Here, r = 10 mm = 0.01 m, l = 1 m,
F = 100 kN = 105 N, Y = 2.0 × 1011 N m–2
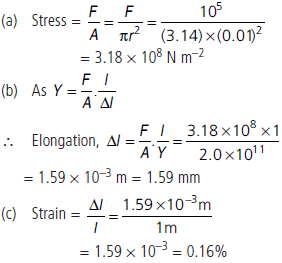
Question. (a) Is it possible to double the length of a metallic wire by applying a force over it?
(b) Is elastic limit a property of the material of the wire?
Answer : (a) No; it is not possible because within elastic limit strain is only of the order of 10–3. Wires actually break much before it is stretched to double the length.
(b) No; it also depends on the radius of the wire.
Question. Stress strain curve for two wires of material A and B are as shown in figure.
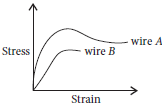
(a) Which material in more ductile?
(b) Which of the two is stronger material?
(c) Which material is more brittle?
Answer : (a) Wire of material A with larger plastic region is more ductile.
(b) For given strain, larger stress is required for A than that for B.
A is stronger than B.
(c) Material with smaller plastic region is more brittle, therefore B is more brittle than A.
Question. What is the percentage increase in the length of a wire of diameter 2.5 mm stretched by a force of 100 kgf? Young’s modulus of elasticity of the wire is 12.5 × 1011 dyne cm–2.
Answer : r = 1.25 mm = 0.125 cm,
F = 100 × 9.8 N = 980 N = 98 × 106 dyne
Y = 12.5 × 1011 dyne cm–2
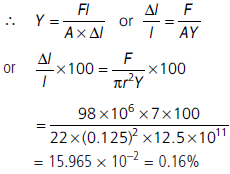
Question. Define the term strain. Why it has no units and dimensions? What are different types of strain?
Answer : The relative change in configuration of a body on applying deforming force is called strain of the body. Different types of strain are
Longitudinal strain : The ratio of change in length to the original length of the body is called longitudinal strain.
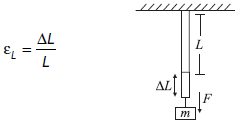
Tangential strain or Shearing strain : The ratio of relative displacement between the opposite faces of the cylinder to the separation between two faces of the cylinder is called tangential strain or shearing strain.
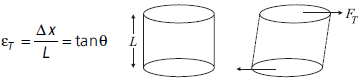
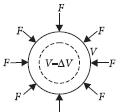
Volumetric strain :
The ratio of change in volume per unit original volume of the body on applying the normal deforming force to surface is called the volumetric strain.
εv = ΔV/V
Question. What is a perfectly plastic body? Give an example.
Answer : If, on removal of deforming force, a body does not regain its original configuration even a little then it is said to be perfectly plastic. For example, putty.
Question. A wire stretches by a certain amount under a load. If the load and radius are both increased to four times, find the stretch caused in the wire.
Answer : Young’s modulus,
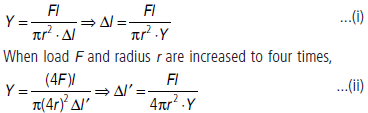
Clearly, if the load and radius are increased to four times, the final elongation will be 1/4th of the initial elongation.
Question. A cable is replaced by another cable of the same length and material but twice the diameter. How will this affect the elongation under a given load?
Answer : Let Y be the Young’s modulus of the material of the wire, L the length and D the diameter. Let the wire be loaded with a mass M. If Δl is the elongation, we can write,
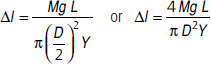
When the diameter is doubled for the same length (L) and mass (M), the elongation is given by,
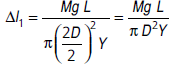
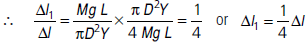
Therefore, the elongation is one-fourth the elongation with the diameter D of the wire.
Question. Compute the bulk modulus of water from the following data : Initial volume = 100.0 litre, pressure increase = 100.0 atm (1 atm = 1.013 × 105 Pa), final volume = 100.5 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
Answer : P = 100 atm = 100 × 1.013 × 105 Pa
Initial volume, V = 100 litre = 100 × 10–3 m3
Final volume, V1 = 100.5 litre = 100.5 × 10–3 m3
ΔV = change in volume = V1 – V
= (100.5 – 100) × 10–3 m3 = 0.5 × 10–3 m3
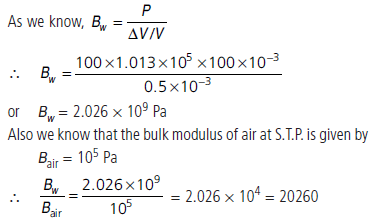
The ratio is too large. It means gases are highly compressible whereas liquids are almost incompressible.
Question. No material is perfectly elastic. Why?
Answer : All materials undergo a change in their original state, howsoever small it may be, after the removal of deforming force. Hence, there is no such material which is perfectly elastic.
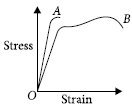
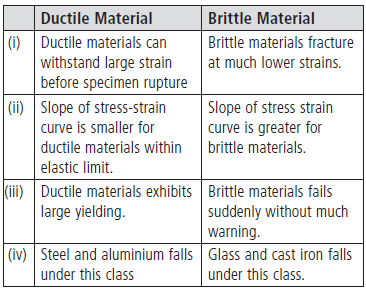
Question. On the basis of stress-strain curves, distinguish between ductile and brittle materials.
Answer : Stress-strain curve of a brittle and ductile materials can be shown in the given figure. In the figure curve A represents brittle material and B represents ductile material. Difference between ductile and brittle materials are :
Question. A cable is replaced by another cable of the same length and material but of half the diameter.
(a) How does this affect its elongation under a given load?
(b) How many times will be the maximum load it can now support without exceeding the elastic limit?
Answer : (a) Young’s modulus,
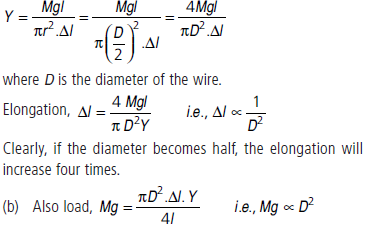
Question. State Hooke’s law. Calculate the fractional compression, DV/V, of water at the bottom of the ocean having depth 3000 m. The bulk modulus of water is 2.2 × 109 N m–2. (Take g = 10 m s–2)
Answer : Hooke’s law : For small deformations the stress developed in the body is directly proportional to the strain of the body.
i.e., Stress ∝ Strain
Stress = K Strain
K = Stress/Strain
where, K = a constant, called modulus of elasticity
Excess pressure at the bottom layer by water column of height h is
P = hpg = 3000 × 1000 × 10
or P = 3 × 107 N m–2 = stress
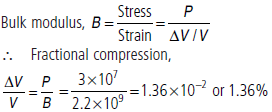
Question. Define modulus of elasticity. Name its three components.
Answer : The ratio of stress and strain is called modulus of elasticity. Modulus of elasticity has three components.
(a) Young’s modulus
(b) Shear modulus
(c) Bulk modulus
Long Answer Type Questions :
Question. Two different types of rubber are found to have the stress-strain curves as shown in figure
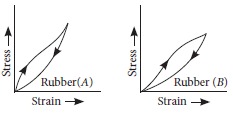
(a) In which significant ways do these curves shown in figure differ from the stress-strain curve of a metal wire ?
(b) A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubber A and B would you prefer to use for this purpose? Why?
(c) Which of the two rubber materials would you choose for a car tyre?
Answer : (a) The stress-strain curves for rubber differ from the stress-strain curve for a metal in following respects:
(i) Hooke’s law is not obeyed even for small stresses.
(ii) There is no permanent set (residual strain) even for large stresses.
(iii) There is large elastic regain for both types of rubber.
(iv) Neither material retraces the curve during unloading.
Thus both materials exhibit elastic hysteresis.
(b) The area of the hysteresis loop is proportional to the energy dissipated by the material as heat when the material undergoes loading and unloading. A material for which the hysteresis loop has larger area would absorb more energy when subjected to vibrations. Therefore to absorb vibrations, we would prefer rubber B.
(c) In car tyre, the energy dissipation must be minimised to avoid excessive heating of the car tyre. As rubber A has smaller hysteresis loop area (and hence smaller energy loss), so it is preferred over B for a car tyre.
Question. A rod of length negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2 respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires?
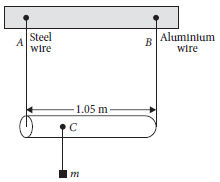
Answer : Suppose the mass m is suspended at distance x from the wire A. Let T1 and T2 be the tensions in the steel and aluminium wires respectively.
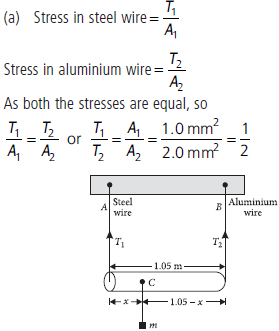
Now the moments about point C are equal because the system is in equilibrium.

Question. (a) A wire 50 cm long and 1 mm2 in cross section has the Young’s modulus, Y = 2 × 1010 N m–2. How much work is done in stretching the wire through 1 mm?
(b) What is the length of a wire that breaks under its own weight when suspended vertically?
Breaking stress = 5 × 107 N m–2
Density of the material of the wire = 3 × 103 kg/m3
Answer : (a) Y = 2 × 1010 N m–2, L = 50 cm = 0.5 m A = 1 mm2 = 10–6 m2
Extension, Δl = 1 mm = 10–3 m,