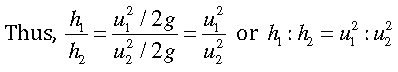Students can read the important questions given below for Motion Class 9 Science. All Motion Class 9 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 9 Science Important Questions provided for all chapters to get better marks in examinations. Science Question Bank Class 9 is available on our website for free download in PDF.
Important Questions of Motion Class 9
Question. A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,
(a) u/g
(b) u2/2g
(c) u2/g
(d) u/2g
Answer
B
Question. If the displacement of an object is proportional to square of time, then the object moves with
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration
Answer
B
Question. A particle is moving in a circular path of radius r. The displacement after half a circle would be:
(a) Zero
(b) πr
(c) 2r
(d) 2πr
Answer
C
Question. In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on straight road
(b) If the car is moving in circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun
Answer
A
Question. Area under a v – t graph represents a physical quantity which has the unit
(a) m2
(b) m
(c) m3
(d) ms–1
Answer
B
Question. Which of the following figures (Fig. 8.3) represents uniform motion of a moving object correctly?
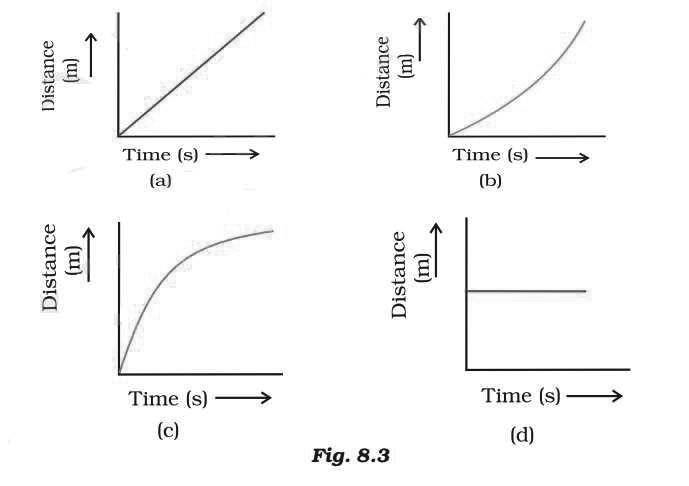
Answer
A
Question. The numerical ratio of displacement to distance for a moving object is
(a) always less than 1
(b) always equal to 1
(c) always more than 1
(d) equal or less than 1
Answer
D
Question. Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 ms–1. It implies that the boy is
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity
Answer
C
Question. Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in Fig. 8.2. Choose the correct statement
(a) Car A is faster than car D.
(b) Car B is the slowest.
(c) Car D is faster than car C.
(d) Car C is the slowest.
Answer
B
Question. Slope of a velocity – time graph gives
(a) the distance
(b) the displacement
(c) the acceleration
(d) the speed
Answer
C
Question. From the given v – t graph (Fig. 8.1), it can be inferred that the object is
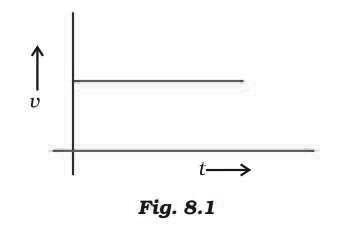
(a) in uniform motion
(b) at rest
(c) in non-uniform motion
(d) moving with uniform acceleration
Answer
A
12. The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero? Justify you answer.
Answer. When the displacement is zero, it does not mean that distance is also zero. Displacement can be zero when the moving object comes back to its original position. Displacement is either equal to or less than distance but distance travelled is always more than zero.
13. How will the equations of motion for an object moving with a uniform velocity change?
Answer. When the object is moving with a uniform velocity, then n = μ and a = 0. In this situation, equation for distance would be as follows:
s = ut and v2 −μ2 = 0
14. A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement–time graph is shown in Fig. 8.4. Plot a velocity–time graph for the same.
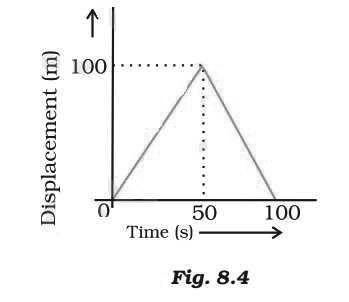
Answer. For the initial 50 second, velocity is 2 m/s. After that, velocity drops of zero; as shown by vertical line in graph.
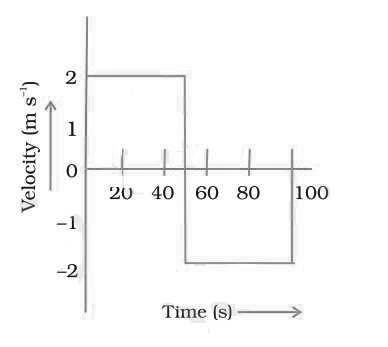
For the next 50 second, velocity is taken in negative because displacement is becoming zero.
15. A car starts from rest and moves along the x-axis with constant acceleration 5 ms–2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest?
Answer. The distance travelled in first 8 s, x1 = 0 + 1/2 (5)(8)2 = 160m.
At this point the velocity v = u+ at= 0 + (5×8) = 40 m s–1
Therefore, the distance covered in last four seconds, x2 = (40×4) m = 160 m
Thus, the total distance x = x1 + x2 = (160 + 160) m = 320 m
16. A motorcyclist drives from A to B with a uniform speed of 30 km h-1 and returns back with a speed of 20 km h-1. Find its average speed.
Answer. Let AB = x, So t1 =, x/30 and t2 = x/20
Total time = t1 + t2 = (5x/60)h
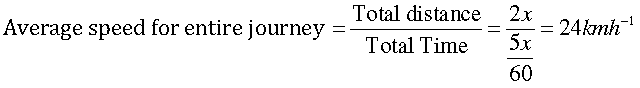
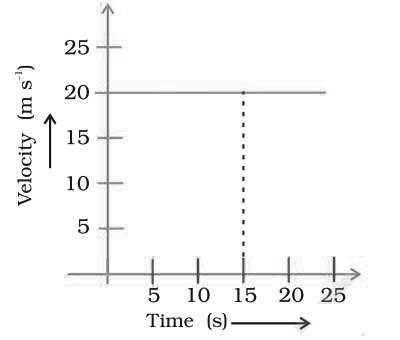
17. The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.
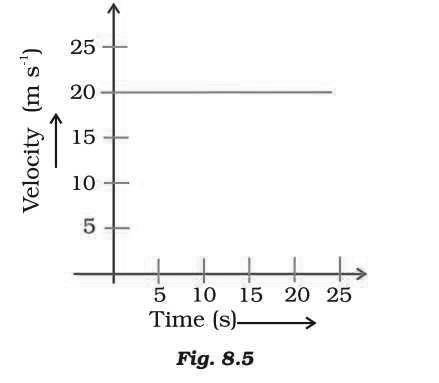
Answer. (i) Since velocity is not changing, acceleration is equal to zero.
(ii) Reading the graph, velocity = 20 ms-1
(iii) Distance covered in 15 seconds, s= u × t= 20 × 15 = 300 m
18. Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height.
Answer.
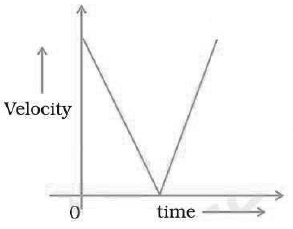
When a stone is thrown upward, its velocity is at maximum. The velocity begins to drops as the stone attains height. Once the stone attains the maximum height, velocity becomes zero. After that, stone begins to fall down. At this points, velocity beings to rise. Velocity is at its maximum when the stone hits the ground.
19. An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height 100 m. What is the difference in their heights after 2 s if both the objects drop with same accelerations? How does the difference in heights vary with time?
Answer. Initial difference in height = (150–100) m = 50 m
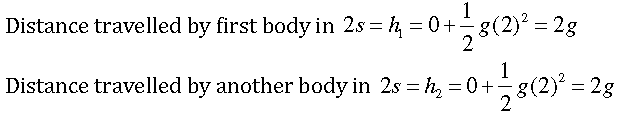
After 2s, height at which the first body will be = h1’=150 – 2g
After 2s, height at which the second body will be = h2’ = 100 – 2g
Thus, after 2s, difference in height = 150 – 2 g – (100 – 2g)
= 50 m = initial difference in height
Thus, difference in height does not vary with time.
20. An object starting from rest travels 20 m in first 2 s and 160 m in next 4 s. What will be the velocity after 7 s from the start?
Answer.
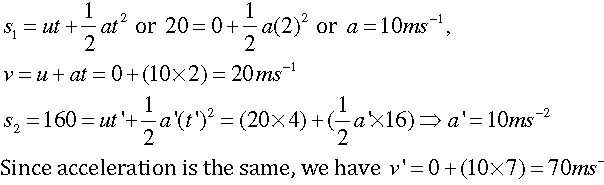
21. Using following data, draw time-displacement graph for a moving object:

Use this graph to find average velocity for first 4 s, for next 4 s and for last 6 s.
Answer.
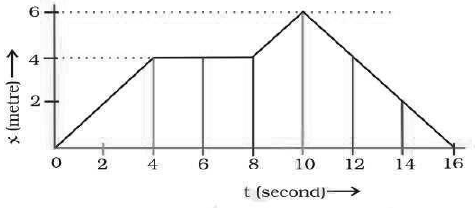
Average velocity for first 4s.
Average velocity = change in displacement / Total time taken
u = 4 – 0 / 4 – 0 = 4 / 4 = lms-1
For next 4s, u = 4 – 4 / 8 – 4 = 0/4 = 0ms-1
(or as x remains the same from 4 to 8 seconds, velocity is zero)
For last 6s, u = 0 – 6 / 16 – 10 = – lms-1
22. An electron moving with a velocity of 5× 104 ms-1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time?
Answer. Given initial velocity, a = 5 x 104 ms−1
And acceleration, a = 104 ms−1
(i) final velocity = u = 2u = 5 x 104 ms-1 = 10 x 104 ms-1
To find t, use u = u + at
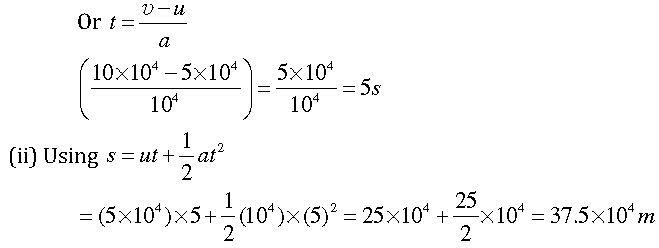
23. Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds.
Answer. Using the equation of motion s = ut + 1/2 at2
Distance travelled in 5s s = u x 5 + (1/2) a x 52
Or s = 5u + 25/2 a — — — — — — — — (i)
Similarly, distance travelled in 4s, s = 4u + 16/2 a — — — — — — — — (ii)
Distance travelled in the interval between 4th and 5th second
= ( s – s ) = (u + 9/2 a) m
24. Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of u21 : u22 (Assume upward acceleration is -g and downward acceleration to be +g.
Answer. We know for upward motion, u2 = u2 – 2gh or h = u2 – u2 / 2g
But at highest point u = 0
Therefore, h = u2 / 2g
For first ball, h1 = u21 / 2g
And for second ball, = u22 / 2g