Please refer to Number System Class 9 Computer Science notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Computer Science books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Computer Science Number System Notes and Questions
Question: What is a numbers system?
Answer: In mathematics, a ‘number system’ is a set of numbers, together with one or more operations, such as addition or multiplication.
A number system is a way of counting things. It’s a way of identifying the quantity of something.
Question: What is expansion method?
Answer: There are a number of ways to convert a number in one base (radix) to the equivalent number in another base. The standard techniques are all variations on three basic methods.
The most straightforward technique is the expansion method. Suppose we wish to convert the binary number 10101.1 to decimal. We may write
10101.12 =1 x 24 + 0 x 23 + 1 x 22 + 0 x 21 + 1 x 20 + 1 x 2-1
= 16 + 0 + 4 + 0 + 1 + 0.5
= 21.510
Question: What is decimal number system? Convert from any base to decimal.
Answer: The Decimal Number System uses base 10. It includes the digits from 0 through 9. It is a positional number system.
Convert from Any Base to Decimal
Let’s think more carefully what a decimal number means. For example, 1234 means that there are four boxes (digits); and there are 4 one’s in the right-most box (least significant digit), 3 ten’s in the next box, 2 hundred’s in the next box, and finally 1 thousand’s in the left-most box (most significant digit). The total is 1234:

Thus, each digit has a value: 10^0=1 for the least significant digit, increasing to 10^1=10, 10^2=100, 10^3=1000, and so forth.
Question: What is positional number system?
Answer: Positional number systems
Our decimal number system is known as a positional number system, because the value of the number depends on the position of the digits. For example, the number 123 has a very different value than the number 321, although the same digits are used in both numbers.
Converting from other number bases to decimal
Other number systems use different bases. The binary number system uses base 2, so the place values of the digits of a binary number correspond to powers of 2. For example, the value of the binary number10011 is determined by computing the place value of each of the digits of the number:
1 0 0 1 1 the binary number
2^4 2^3 2^2 2^1 2^0 place values
So the binary number 10011 represents the value
(1 * 2^4) + (0 * 2^3) + (0 * 2^2) + (1 * 2^1) + (1 * 2^0)
= 16 + 0 + 0 + 2 + 1
= 19
The same principle applies to any number base. For example, the number 2132 base 5 corresponds to
2 1 3 2 number in base 5
5^3 5^2 5^1 5^0 place values
Converting from decimal to other number bases
In order to convert a decimal number into its representation in a different number base, we have to be able to express the number in terms of powers of the other base. For example, if we wish to convert the decimal number 100 to base 4, we must figure out how to express 100 as the sum of powers of 4.
100 = (1 * 64) + (2 * 16) + (1 * 4) + (0 * 1)
= (1 * 4^3) + (2 * 4^2) + (1 * 4^1) + (0 * 4^0)
Then we use the coefficients of the powers of 4 to form the number as represented in base 4:
100 = 1 2 1 0 base 4
Repeated Division Method:
One way to do this is to repeatedly divide the decimal number by the base in which it is to be converted, until the quotient becomes zero. As the number is divided, the remainders – in reverse order – form the digits of the number in the other base.
Example: Convert the decimal number 82 to base 6:
82/6 = 13 remainder 4
13/6 = 2 remainder 1
2/6 = 0 remainder 2
The answer is formed by taking the remainders in reverse order: 2 1 4 base 6
Question: What is Binary number system?
Answer: The binary number system works like the decimal number system except the Binary Number System:
uses base 2
includes only the digits 0 and 1
Number Base Conversion
Binary to Decimal
It is very easy to convert from a binary number to a decimal number. Just like the decimal system, we multiply each digit by its weighted position, and add each of the weighted values together. For example, the binary value 1100 1010 represents:
1*2^7 + 1*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 =
1 * 128 + 1 * 64 + 0 * 32 + 0 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 0 * 1 =
128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 =202
Decimal to Binary
To convert decimal to binary is slightly more difficult. There are two methods, that may be used to convert from decimal to binary.
1. Repeated division by 2,
2. Repeated subtraction by the weighted position value.
Repeated Division By 2
For this method, divide the decimal number by 2, if the remainder is 0, on the side write down a 0. If the remainder is 1, write down a 1. This process is continued by dividing the quotient by 2 and dropping the previous remainder until the quotient is 0.
When performing the division, the remainders which will represent the binary equivalent of the decimal number are written beginning at the least significant digit (right) and each new digit is written to more significant digit (the left) of the previous digit. Consider the number 2671.
Octal Number System
The Octal Number Base System
Although this was once a popular number base but it is rarely used today. The Octal system is based on the binary system with a 3-bit boundary. The Octal Number System:
uses base 8
includes only the digits 0 through 7
(any other digit would make the number an invalid octal number)
Binary to Octal Conversion
It is easy to convert from an integer binary number to octal. This is accomplished by: Break the binary number into 3-bit sections from the LSB to the MSB.
Convert the 3-bit binary number to its octal equivalent.
For example, the binary value 1010111110110010 will be written:

Octal to Binary Conversion
It is also easy to convert from an integer octal number to binary. This is accomplished by:
Convert the decimal number to its 3-bit binary equivalent.
Combine the 3-bit sections by removing the spaces.
For example, the octal value 127662 will be written:
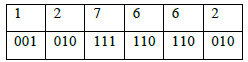
This yields the binary number 001010111110110010 or 00 1010 1111 1011 0010 in our more readable format.
Octal to Decimal Conversion
To convert from Octal to Decimal, multiply the value in each position by its Octal weight and add each value. Using the value from the previous example, 127662, we would expect to obtain the decimal value 44978.

Decimal to Octal Conversion
To convert decimal to octal is slightly more difficult. The typical method to convert from decimal to octal is repeated division by 8.
We may also use repeated subtraction by the weighted position value; it is more difficult for large decimal numbers.
Repeated Division By 8
For this method, divide the decimal number by 8, and write the remainder on the side as the least significant digit.
This process is continued by dividing the quotient by 8 and writing the remainder until the quotient is 0.
When performing the division, the remainders which will represent the octal equivalent of the decimal number are written beginning at the least significant digit (right) and each new digit is written to the next more significant digit (the left) of the previous digit. Consider the number 44978.

The Hexadecimal Number Base System .
The Hexadecimal system is based on the binary system using a Nibble or 4-bit boundary.
The Hexadecimal Number System:
The hexadecimal is base 16 numbering system.
- Uses base
- 16 Includes only the digits 0 through 9 and the letters A, B, C, D, E, and F
Hexadecimal numbers offer the two features:
- Hex numbers are very compact
- It is easy to convert from hex to binary and binary to hex
In the Hexadecimal number system, the hex values greater than 9 carry the following decimal value:

This table provides all the information you’ll ever need to convert from one number base into any other number base for the decimal values from 0 to 16.
Hexadecimal number into a binary number Conversion:
To convert a hexadecimal number into a binary number, simply break the binary number into 4-bit groups beginning with the LSB and substitute the corresponding four bits in binary for each hexadecimal digit in the number.
For example, to convert 0ABCDh into a binary value, simply convert each hexadecimal digit according to the table above. The binary equivalent is:
0ABCDH = 0000 1010 1011 1100 1101
To convert a binary number into hexadecimal format is almost as easy. The first step is to pad the binary number with leading zeros to make sure that the binary number contains multiples of four bits. For example, given the binary number 10 1100 1010, the first step would be to add two bits in the MSB position so that it contains 12 bits. The revised binary value is 0010 1100 1010.
The next step is to separate the binary value into groups of four bits, e.g., 0010 1100 1010. Finally, look up these binary values in the table above and substitute the appropriate hexadecimal digits, e.g., 2CA.
The weighted values for each position is as follows:
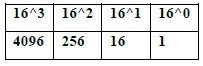
Binary to Hex Conversion:
It is easy to convert from an integer binary number to hex. This is accomplished by:
Break the binary number into 4-bit sections from the LSB to the MSB.
Convert the 4-bit binary number to its Hex equivalent.
For example, the binary value 1010111110110010 will be written:
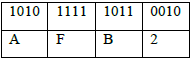
Hex to Binary Conversion:
It is also easy to convert from an integer hex number to binary. This is accomplished by:
Convert the Hex number to its 4-bit binary equivalent.
Combine the 4-bit sections by removing the spaces.
For example, the hex value 0AFB2 will be written:

This yields the binary number 1010111110110010 or 1010 1111 1011 0010 in our more readable format.
Hex to Decimal Conversion:
To convert from Hex to Decimal, multiply the value in each position by its hex weight and add each value. Using the value from the previous example, 0AFB2H, we would expect to obtain the decimal value 44978.

Decimal to Hex Conversion:
To convert decimal to hex is slightly more difficult. The typical method to convert from decimal to hex is repeated division by 16. While we may also use repeated subtraction by the weighted position value, it is more difficult for large decimal numbers.
Repeated Division By 16
For this method, divide the decimal number by 16, and write the remainder on the side as the least significant digit. This process is continued by dividing the quotient by 16 and writing the remainder until the quotient is 0. When performing the division, the remainders which will represent the hex equivalent of the decimal number are written beginning at the least significant digit (right) and each new digit is written to the next more significant digit (the left) of the previous digit. Consider the number 44978.

As you can see, we are back with the original number. That is what we should expect.
Question: Define one’s and two’s complement.
One’s complement:
One‟s complement of a binary number is obtained by changing all 0‟s to 1‟s and all 1‟s to 0‟s.
To negate a number, replace all zeros with ones, and ones with zeros – flip the bits. Thus, 12 would be 00001100, and -12 would be 11110011.
Two’s complement:
Two‟s complement of a binary number is obtained by taking one‟s complement and then adding 1 in the result.
Calculation of 2’s Complement
To calculate the 2’s complement of an integer, invert the binary equivalent of the number by changing all of the ones to zeroes and all of the zeroes to ones (also called 1’s complement), and then add one.
For example,

2’s Complement Addition
Two’s complement addition follows the same rules as binary addition.
For example,

2’s Complement Subtraction
Two’s complement subtraction is the binary addition of the minuend to the 2’s complement of the subtrahend (adding a negative number is the same as subtracting a positive one).
For example,

2’s Complement Multiplication
Two’s complement multiplication follows the same rules as binary multiplication.
For example,

2’s Complement Division
Two’s complement division is repeated 2’s complement subtraction. The 2’s complement of the divisor is calculated, then added to the dividend. For the next subtraction cycle, the quotient replaces the dividend. This repeats until the quotient is too small for subtraction or is zero, then it becomes the remainder. The final answer is the total of subtraction cycles plus the remainder.
For example,
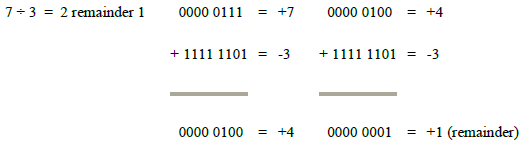
Question: what are main data types used in different computer applications? Explain.
Answer: Data types used in computer application:
Almost all programming languages explicitly include the notion of data type, though different languages may use different terminology. Common data types may include:
Integers: In computer science, the term integer is used to refer to a data type which represents some finite subset of the mathematical integers
Booleans: In computer science, the Boolean or logical data type is a data type, having two values (usually denoted true and false),
characters: In computer and machine-based telecommunications terminology, a character is a unit of information that roughly corresponds to symbol, such as in an alphabet in the written form of a natural language.
Floating-point numbers: In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values.
Alphanumeric Strings: In computer programming, a string is traditionally a sequence of characters,
Question: Define codes. What are the types of codes used in computer?
Answer: Codes
When numbers, letters or words are represented by a special group of symbols, we say they are being encoded and the group of system is called “Code”.
Types of Codes
The codes include Binary code, Binary-coded-decimal code (BCD), and alpha numeric codes. Alphanumeric codes include ASCII and EBCDIC.
ASCII Code
ASCII stands for American Standard Code for Information Interchange. It is a 7-bit code used to handle alphanumeric data. This code allows manufacturers to standardize input/output devices such as keyboard, printers, visual display units etc. An extension of ASCII code uses 8-bits called as ASCII-8 code with an extra 8th-bit as a parity bit to make the total number of 1’s either odd or even.
EBCDIC Code
EBCDIC (Extended Binary Coded Decimal Interchange Code) is an extended form of BCD (Binary Coded Decimal), which can represent only 16 characters because it is a 4-bit code. EBCDIC is an 8-bit code, so it can represent 256 different characters. It was developed by IBM and is used in most IBM models and many other computers.
BCD
“In BCD, a digit is usually represented by four bits which, in general, represent the values/digits/characters 0–9. Other bit combinations are sometimes used for a sign or other indications.”
Basically, BCD is just a representation of a single number using 4 Bits Binary
Example:
9 in BCD = 1001
8 in BCD = 1000
EXPRESSIONS
An expression is a combination of constants and variables linked by arithmetic operators like (+, -, *, /, \). Expressions are used to perform different operations. The expressions are evaluated from left to right but some operators have priority over the others. Parenthesis are evaluated first then multiplication and division have the same priority fr om left to right. Similarly the addition and subtraction are evaluated with equal priorities. If all the operators are used in an expression have the same priority then the expression be executed from left to right.
The expressions can be of three types.
* Arithmetic expressions
* Logical expressions
* Relational expressions.
ARITHMETICAL EXPRESSIONS
In an arithmetic expression the following operators are used in conjunction with the operands. Symbol Meaning
+ Addition
– Subtraction
* Multiplication
/ Division
^ Exponentiation
( Left parenthesis
) Right parenthesis
RELATIONAL EXPRESSION
A Relational expression is composed of operands linked by the relational operators. The relational operators used in the rela tional expression are given.
Symbol Meaning
= equal to
> greater than
< less than
<> not equal to
>= greater than or equal to
<= less than or equal to
Example
A > B
B <> C
LOGICAL EXPRESSIONS
When a selections is based upon one or more condition being true. It is possible to combine the condition together using logical operators and the resulting condition would either be true or false the most commonly used logical operators are AND, OR and NOT.
COMPUTER LANGUAGE
Language is a system for representation and communication of information or data. Like human beings, a language or signal is required to communicate between two persons. Similarly, we cannot obtain any result by computer without langtage. Computer does not understand directly what we are communicating with computer as English or Arabic, it understands only machine language (binary codes 0-1). Computer translates English language into machine codes through interpreter then process instructions and give us the results.
The computer languages can be divided into two main levels.
* Machine language (0-1)
* Symbolic language (A-Z)
Symbolic languages are further divide into two main levels
* High-level language
* Low-level language
Machine Language
Although computers can be programmed to understand many different computer language. There is only one language understood by the computer without using a translation program. This language is called the machine language or the machine codes.
Machine codes are the fundamental language of the computer and is normally written as strings of binary 0-1.
ADVANTAGES AND LIMITATIONS OF MACHINE LANGUAGE Advantages:
Programs written in machine language can be executed very fast by the computer. This is mainly because machine instructions are directly understood by the CPU and no translation of program is required.
Disadvantages:
However, writing a program in machine language has several disadvantage.
Machine Dependent
Because the internal design of every type of computer is different from every other type of computer and needs different electrical signals to operate. The machine language also is different from computer to computer.
Difficult To Program
Although easily used by the computer, machine language is difficult to program. It is necessary for the programmer either to memorize the dozens of code number for the commands in the machine‟s instruction set or to constantly refer to a reference card.
Difficult to Modify
It is difficult to correct or modify machine language programs. Checking machine instructions to locate errors is difficult as writing them initially.
In short, writing a program in machine language is so difficult and time consuming.
Symbolic Languages
In symbolic languages, alphabets are used (a-z). symbolic languages are further divide into two main levels.
* High level languages
* Low level languages
LOW LEVEL LANGUAGE
A language which is one step higher than machine language in human readability is called Assembly Language or a low-level language. In an assembly language binary numbers are replaced by human readable symbols called mnemonics. Thus a low-level language is better in understanding than a machine language for humans and almost has the same efficiency as machine language for computer operation. An assembly language is a combination of mnemonic, operation codes and symbolic codes for addresses. Each computer uses and has a mnemonic code for each instruction, which may vary from computer to computer. Some of the commonly used codes are given in the following table.
COMMAND NAME MNEMONIC
Add – ADD Subtract – SUB
Multiply – MUL
Compare Registry – CR
Compare – COMP
Branch Condition -BC
Code Register -LR
Move Characters -MVE Store Characters -STC Store Accumulator – STA
An assembly language is very efficient but it is difficult to work with and it requires good skills for programming. A program written in an assembly language is translated into a machine language before execution. A computer program which translates any assembly language into its equivalent machine code is known as an assembler.
HIGH – LEVEL LANGUAGE
A language is one step higher than low-level languages in human readability is called high-level language. High – level languages are easy to understand. They are also called English oriented languages in which instruction are given using words. Such as add, subtract, input, print, etc. high level language are very easy for programming, programmer prefer them for software designing that‟s why these languages are also called user‟s friendly languages. Every high level language must be converted into machine language before execution; therefore every high level language has its own separate translating program called compiler or interpreter. That‟s why some time these languages are called compiler languages. COBOL, BASIC, PASCAL, RPG, FORTRAN are some high level languages.
INTERPRETER
An interpreter is a set of programs which translates the high-level language into machine acceptable form. The interpreters are slow in speed as compared to compilers. The interpreter takes a single line of the source code, translates that line into object code and carries it out immediately. The process is repeated line by line until the whole program has been translated and run. If the program loops back to earlier statements, they will be translated afresh each time round. This means that both the source program and the interpreter must remain in the main memory together which may limit the space available for data. Perhaps the biggest drawback of an interpreter is the time it takes to translate and run a program including all the repetition which can be involved.
PROGRAM DEVELOPMENT PROCESS
In order to develop a computer program, a programmer has to go through the following stages:
- DEFINING AND ANALYSING THE PROBLEM
In this step a programmer studies the problem and decides how the problem will be best solved. Studying a problem is necessary because it helps a programmer to decide about:
* The facts and figures to be collected.
* The way in which the program will be designed.
* The language in which the program will be most suitable.
* What is the desired output and in which form it is needed, etc. - DESIGNING THE ALGORITHM
An algorithm is a set of instructions or sequence of steps that must be carried out before a programmer starts preparing his program. The programmer designs an algorithm to help visualize possible alternatives in a program. - FLOWCHARTING
A flow chart is a graphical representation of a program which helps a programmer to decide on various data processing procedures with the help of labeled geometrical diagrams. A flow chart is mainly used to describe the complete data processing system including the hardware devices and media used. It is very necessary for a programmer to know about the available devices before developing a program. - CODING OR WRITING THE PROGRAM
The next job after analyzing the problem is to write the program in a high-level language, usually called coding. This is achieved by translating the flow chart in an appropriate high-level language, of course according to the syntax rules of the language. - TEST EXECUTION
The process of execution of any program to find out for errors or bugs (mistakes) is called test execution. This is very important because it helps a programmer to check the logic of the program and to ensure that the program is error -free and workable. - DEBUGGING
It is a term which is used extensively in programming. Debugging is the process of detecting, locating and correcting the bugs by running the programs again and again. - FINAL DOCUMENTATION
It is written information about any computer software. Final document guides the user about how to use the program in the most efficient way.
MODES OF OPERATION
There are two modes of operation for BASIC. The mode that you are in determines what BASIC will do with the instruction you give it. When you start BASIC you receive the OK prompt. You then have two modes available to you immediately.
DIRECT MODE
In the direct mode BASIC acts like a calculator. No line numbers are required. Direct mode is not of course the main purpose of BASIC, but it is useful at times particularly when you are debugging program or short problems in which you want to perform quick calculation e.g., PRINT 3+4.
INDIRECT MODE
In this mode you first put a line number on each statement. Once you have a program you can run it and get your results. The indirect mode saves your instructions in the computer along with their line number, you can execute the program as many times as you wish simply by typing RUN.
STEPS OF PROGRAMMING
There are five steps in preparing a computer programme which are also called ABCDE of Programming.
ANALYSIS
In this step the system analyst tries to become familiar with the problem. He has to study the problem and prepare some notes upon that problem. He also notes that what is given, what is required and what will computer can do.
BLOCKING
In this step the programmer converts the analyst report to a series of steps through which the computer will give the required result. The steps are commonly known as Algorithm. There are different ways to write those detailed sequential steps. The most common method used is flow charting. A flow chart is symbolic representation of flow of a programme.
CODING
In this step the programmer writes the program in any computer language. This step is known as coding. After this program is fed into the computer and is compiled with the help of a given compiler.
DEBUGGING
Debugging is a step in which a programmer corrects a syntax error which may come after the compilation.
TESTING
Testing is a step where the programmer is finally testing the program for execution (there may be any logical mistake which compiler cannot trace).
EXECUTION
In this step we send the program for execution where company‟s data will be fed and process.
INTRODUCTION TO BASIC
BASIC is a high level language used for purpose of writing a program on a computer. It stands for Beginners All-purpose Symbolic Instruction Code. BASIC is an easy to use “friendly” language where instruction resembles elementary, algebraic formulas and certain English keywords such Let, Read, Print, Goto etc.
HISTORY OF BASIC
The language was developed at Dartmouth College in 1967, under the direction of John Kemeny and Thomas Kurtz. It was quickly discovered and adopted. All the major computer manufacturers offered their own version of BASIC for their particular computers.
In 1978, the American National Standard Institute standardized an essential subset of BASIC in order to promote uniformity from one version of BASIC into another.
In recent years some new version of BASIC have been developed which included a variety of features that are not included in more traditional versions.
Data
The word data is derived from Latin language. It is plural of Datum (But Data is usually used as a singular term.) Datum (singular) – Data (plural). Data is any collection of facts of figures. The data is the raw material to be processed by a computer.
Example
Names of students, marks obtained in the examination, designation of employees, addresses, quantity, rate, sales figures or anything that is input to the computer is data. Even pictures, photographs, drawings, charts and maps can be treated as data. Computer processes the data and produces the output or result.
Types of Data
Mainly Data is divided into two types:
- Numeric Data
- Character Data
Numeric Data
The data which is represented in the form of numbers is known as Numeric Data. This includes 0-9 digits, a decimal point (.), +,/, – sign and the letters “E” or “D”. The numeric data is further divided into two groups:
- Integer Data
- Real Data
Integer Data
Integer Data is in the form of whole numbers. It does not contain a decimal point, however it may be a positive or a negative number.
Example
Population of Pakistan, numbers of passengers traveling in an airplane, number of students in a class, number of computer in a lab etc.
2543, 7, -60, 5555, 0, + 72 etc
Real Data
Real data is in the form of fractional numbers. It contains a decimal point. It can also be positive or negative number. Real Data is further divided into two types.
a. Fixed Point Data
b. Floating Point Data
(a) Fixed Point Data
Fixed point data may include digits (0–9), a decimal point, + / – sign. Example Percentage of marks, weight, quantity temperature etc.
-23.0007, 0.0002, + 9243.9, 17013 etc
(b) Floating Point Data
Floating point data may include digits (0-9), decimal point, + / – sign and letters “D”, “d”, “E”, or “e”. The data, which is in the exponential form, can be represented in the floating point notation.
Example
Speed of light, mass of atomic particles, distance between stars and etc.
1.602 x 10(-19) (Charge of electron in coulomb) – Here -19 = power
The value can be feed into the computer as 1.602 E-19.
Character Data
Character data falls into two groups.
- String Data
- Graphical Data
String Data
String data consists of the sequence of characters. Characters may be English alphabets, numbers or space. The space, which separates two words, is also a character. The string data is further divided into two types.
- Alphabetic Data
- Alphanumeric Data
(a) Alphabetic Data
The data, which is composed of English alphabets, is called alphabetic data. Names of people, names of places, and names of items are considered alphabetic data.
For example : Ahmed, Hyderabad, Chair etc
(b) Alphanumeric Data
The data that consists of alphabets as well as numerals and some special characters is called alphanumeric data. Address, employee’s code, etc are alphanumeric data.
For example: 10/B, Block No 2, E103 etc.
Graphical Data
It is possible that pictures, charts and maps can be treated as data. The scanner is normally used to enter this type of data. The common use of this data is found in the National Identity Card. The photographs and thumb impression are scanned and stored into the computer to identify a person.
Number System
The number system is the system of counting and calculation. Number system is based on some characters called digits. Ea ch number is made up of these characters. The number of digits a system uses is called its base or radix. For example the number system we use in our daily life is called Decimal System. Its base is 10 (As the name ‘Deci’ implies which mean that it uses 10 digits (i.e. 0-9)
Codes
When numbers, letters or words are represented by a special group of symbols, we say they are being encoded and the group of system is called “Code”.
Types of Codes
The codes include Binary code, Binary-coded-decimal code (BCD), and alpha numeric codes. Alphanumeric codes include ASCII and EBCDIC.
ASCII Code
ASCII stands for American Standard Code for Information Interchange. It is a 7-bit code used to handle alphanumeric data. This code allows manufacturers to standardize input/output devices such as keyboard, printers, visual display units etc. An extension of ASCII code uses 8-bits called as ASCII-8 code with an extra 8th-bit as a parity bit to make the total number of 1’s either odd or even.
EBCDIC Code
EBCDIC (Extended Binary Coded Decimal Interchange Code) is an extended form of BCD (Binary Coded Decimal), which can represent only 16 characters because it is a 4-bit code. EBCDIC is an 8-bit code, so it can represent 256 different characters. It was developed by IBM and is used in most IBM models and many other computers.
Machine Language
Machine language is the only language that a compute understands directly without any translation, it is the binary language. It is the language of 0’s and 1’s . It consists of strings of binary numbers.
The binary codes are very difficult to memorize for human beings that is why a machine language is cumbersome for a user.
Difference Between a High-Level Language and Low-Level Language
High-Level Languages
High-Level language are more suitable for human use than machine languages and enable the programmer to write instructions easily using English words and familiar mathematical symbols. These symbolic languages are called High-Level languages. These high-level languages consist of simple English sentences, which are very easy to understand and memorize for human being.
Low-Level Languages
Both the machine and assembly languages are called Low-Level Languages. An assembly language is one step higher than the machine language in human readability. A machine language consists of totally of numbers and is almost impossible for humans to read. In an assembly language, some of these numbers are replaced by human readable symbols called language for humans and almost of the same efficiency as machine language for computer operations. An assembly language is a combination of mnemonic operation codes and symbolic codes for address.
Assembly language is very difficult but it requires good skills for programming. A program written in an assembly language is translated into a machine language before computer can understand and execute it. A computer program, which translates an assembly language program into its equivalent machine language, is called assembler.
A program can be written in much shorter time and much precisely when a high level language is used. A program written in a high level language can be executed in any computer system, which has a compiler for that programming language.


