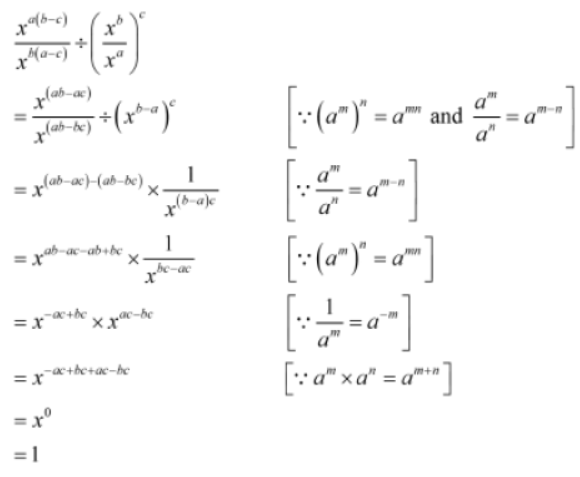Please refer to Number Systems Class 9 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Mathematics Number Systems Notes and Questions
History and Evolution of Irrational Numbers
The existence of irrationality in numbers was accepted by Indian mathematicians as far back as 7th century BC when Manava, an author of the Indian geometric text Sulbasutras, discovered (while finding the hypotenuse of a right-angled triangle) that it is not possible to accurately calculate the square roots of numbers like 2 and 8. It is, however, the Pythagorean school of Greek mathematicians, or the Pythagoreans, who are credited with discovering irrational numbers sometime in 400 BC. In 5th century AD, the great Indian mathematician Aryabhata suggested that the value of π is incommensurable. Later, in the 1700s, a Swiss mathematician named Lambert and a French mathematician named Legendre proved π to be irrational.
In this way, a long line of mathematicians helped shed light on the concept of irrational numbers. These mathematicians questioned the rationality of those numbers that cannot be written in the form of a ratio of integers.The Pythagoreans were the first to actually prove a number to be irrational and this number was √2 . The set of all irrational numbers is denoted by Q.
Go through this lesson to get a basic idea about the irrationality of numbers.
Whiz Kid
Golden ratio
Two quantities are said to be in the golden ratio if the ratio of the sum of those quantities to the larger quantity is the same as the ratio of the larger quantity to the smaller one. Let us understand this concept.
Say a and b are two line segments that are in the golden ratio.
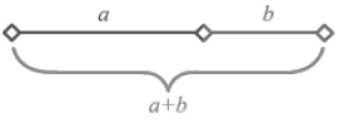
Therefore, a+b/a = a/b
The golden ratio is represented by the Greek letter ‘ Φ ’ (phi), where Φ = 1+√5/2 = 1.61803…. an irrational number.
The golden ratio is also known as ‘the golden mean’ and ‘the golden section’. This ratio is used not only in mathematics but also in biology, art, music, architecture and in various other branches of science.
Did You Know?
Pi is a constant value that is equal to the ratio of the circumference of a circle to its diameter. It is an irrational number represented by the Greek letter ‘π’. This symbol was proposed by a Welsh mathematician named William Jones in 1706. The value of pi is approximately equal to 22/7
The Great Pyramid of Giza was constructed with a perimeter of about 1760 cubits and a height of about 280 cubits. The ratio of the perimeter to the height, i.e., 1760/280 is approximately equal to 6.285, which is almost equal to 2π. This is cited by some as the proof that the people who built the pyramid knew about the special ratio represented by π.
Since π is closely related to the circle, it is found in many geometric and trigonometric formulae. It is also used in many other scientific formulae such as in thermodynamics, the number theory, mechanics and electromagnetism.
Know Your Scientist

Know More
1. No rational number (e.g. 5) is irrational and no irrational number (e.g.√5) is rational as the properties of one are different from those of the other.
2. There are no smallest or largest numbers in the groups of rational and irrational numbers.
Did You Know?
The need for numbers
Initially, humans used to keep count of different things by using pebbles, sticks or fingers.
Later, they began using tally marks for counting purposes. The system of tally marks is not based on the concept of place value. This made the counting and representation of large numbers difficult. Thus grew the need for simpler counting systems and, with the passage of time, the Roman, Hindu-Arabic and other numeral systems came into being.
Solved Examples
Easy
Example 1: Check whether the given numbers are rational or irrational.
i) (7-2√5) + 2√5
ii) 0
iii) √49/81
iv) √289
v) 5.012896896896…
vi) 7.1931931934…
vii) 0.0787887888…
Solution:
i) (7-2√5) + 2√5
= 7-2√5 + 2√5
= 7
= 7/1
This number is of the form p/q , where p = 7 and q = 1 are integers and q ≠ 0.
Hence, (7-2√5) + 2√5 is a rational number.
ii) 0 = o/1
This number is of the form p/q, where p = 0 and q = 1 are integers and q ≠ 0.
Hence, 0 is a rational number.
iii) √49/81 = 7/9
This number is of the form p/q, where p = 7 and q = 9 are integers and q ≠ 0.
Hence, √49/81 is a rational number.
iv) √289 = 17 = 17/1
This number is of the form p/q , where p = 17 and q = 1 are integers and q ≠ 0.
Hence, √289 is a rational number.
v) 5.012896896896…
This decimal number is non-terminating and repeating (i.e., the group of digits 896 repeats after the decimal point). Hence, it is a rational number.
vi) 7.1931931934…
This decimal number appears to be non-terminating and repeating, but it is in fact nonterminating and non-repeating. The group of digits ‘193’ repeats twice after the decimal point and then a new set of digits ‘1934’ can be seen. There is no one digit or group of digits that keeps repeating itself after the decimal point. Hence, this number is irrational.
vii) 0.0787887888…
This decimal number is non-terminating and non-repeating. In it, the 8s between the 7s keep increasing by one. Hence, this number is irrational.
Medium
Example 1:
Consider the given set of numbers.

In set A, there are a rational numbers and b irrational numbers. Show that a2 − b2 = a + b.
Solution:
2.6666… is non-terminating and repeating (i.e., the digit ‘6’ is repeated after the decimal point). Hence, it is a rational number.
2157/625 is of the form p/q, where p = 2157 and q = 625 are integers and q ≠ 0. Hence, it is a rational number.
0.181881888… is non-terminating and non-repeating. In it, the 8s between the 1s keep increasing by one. Hence, it is an irrational number.
35/16 is of the form p/q, where p = 35 and q = 16 are integers and q ≠ 0. Hence, it is a rational number.
0.14201421… is non-terminating and non-repeating. Hence, it is an irrational number.
√2/2√8 = √2/4√2 = 1/4 , which is of the form p/q , where p = 1 and q = 4 are integers and q ≠ 0.
Hence, it is a rational number.
We know that π is an irrational number.
Thus, in set A, we have a = 4 and b = 3.
a2 − b2 = (a + b) (a − b)
⇒ a2 − b2 = (a + b) (4 − 3)
⇒ a2 − b2 = (a + b) (1)
⇒ a2 − b2 = (a + b)
Decimal Expansions of Rational Numbers
The Need for Converting Rational Numbers into Decimals
A carpenter wishes to make a point on the edge of a wooden plank at 95 mm from any end.
He has a centimeter tape, but how can he use that to mark the required point?
Simple! He should convert 95 mm into its corresponding centimeter value, i.e., 9.5 cm and then measure and mark the required length on the wooden plank.
This is just one of the many situations in life when we face the need to convert numbers into decimals. In this lesson, we will learn to convert rational numbers into decimals, observe the types of decimal numbers, and solve a few examples based on this concept.
Two rational numbers a/b and c/d are equal if and only if ad = bc.
Take, for example, the rational numbers 2/4 and 3/6 . Let us see if they are equal or not.
Here, a = 2, b = 4, c = 3 and d = 6
Now, we have:
ad = 2 × 6 = 12
bc = 4 × 3 = 12
Since ad = bc, we obtain 2/4 = 3/6 .
Rational Numbers as Division of Integers
We know that the form p/q represents the division of integer p by the integer q. By solving this division, we can find the decimal equivalent of the rational number p/q . Now, let us convert the numbers 5/8 , 4/3 and 2/7 into decimals using the long division method.

While the remainder is zero in the division of 5 by 8, it is not so in case of the other two divisions. Thus, we can get two different cases in the decimal expansions of rational numbers.
Observing the Decimal Expansions of Rational Numbers
We can get the following two cases in the decimal expansions of rational numbers.
Case I: When the remainder is zero
In this case, the remainder becomes zero and the quotient or decimal expansion terminates after a finite number of digits after the decimal point. For example, in the decimal expansion of 5/8 , we get the remainder as zero and the quotient as 0.625.
Case II: When the remainder is never zero
In this case, the remainder never becomes zero and the corresponding decimal expansion is non-terminating. For example, in the decimal expansions of 4/3 and 2/7 , we see that the remainder never becomes zero and their corresponding quotients are non-terminating decimals.
When we divide 4 by 3 and 2 by 7, we get 1.3333… and 0.285714285714… as the respective quotients. In these decimal numbers, the digit ‘3’ and the group of digits ‘285714’ get repeated. Therefore, we can write 4/3 = 1.3333 …. = 1.3 and 2/7 = 0.285714285714… = —0.285714 . Here, the symbol indicates the digit or group of digits that gets repeated.
Solved Examples
Example 1: Write the decimal expansion of 1237/25 and find if it is terminating or nonterminating and repeating.
Solution: Here is the long division method to find the decimal expansion of 1237/25
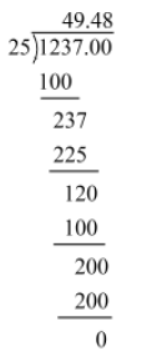
Hence, the decimal expansion of 1237/25 is 49.48. Since the remainder is obtained as zero, the decimal numberis terminating.
Example 2: Write the decimal expansion of 2358/27 and find if it is terminating or non-terminating and repeating.
Solution: Here is the long division method to find the decimal expansion of 2358/27

Hence, the decimal expansion of 2358/27 is 87.33…. Since the remainder 9 is obtained again and again, the decimal numberis non-terminating and repeating. The decimal number can also be written as 87.3 .
Medium
Example 1: Find the decimal expansion of each of the following rational numbers and write the nature of the same.
1. 65/101
2. 923/400
3. 37/99
4. 67/100
Solution:
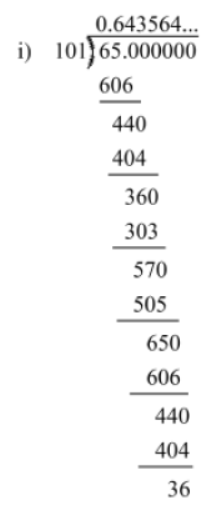
We have 65/101 = 0.64356435… = 0.—6435
The group of digits ‘6435’ repeats after the decimal point. Hence, the decimal expansion of the given rational number is non-terminating and repeating.

We have 923/400 = 2.3075
Hence, the given rational number has a terminating decimal expansion.
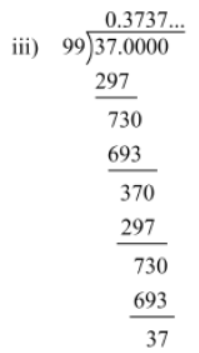
We have 37/99 = 0.3737… = 0.—37
The pair of digits ‘37’ repeats after the decimal point. Hence, the decimal expansion of the given rational number is non-terminating and repeating.

We have 67/100 = 0.67
Hence, the given rational number has a terminating decimal expansion.
Decimal Expansion of Irrational Numbers
Facing Irrational Numbers in Life
Anu has a piece of land in the backyard of her house. She calls a mason and tells him to construct a square-shaped kitchen garden covering an area of 7m2.

After a quick mental calculation, the mason replies that he cannot construct the garden as per Anu’s specification. Why do you think the mason says this?
To answer this question, let us first see the calculation performed by the mason in his head.
Anu wants a square garden with an area of 7m2.
Area of a square = Side × Side
⇒ (Side)2 = 7m2
∴ Side = √7
Now, we can find only an approximate value of √7 as it is an irrational number. We cannot ascertain the exact value of an irrational number as its decimal expansion is nonterminating and non-repeating. This is why the mason says that it is not possible to obtain a square garden as per Anu’s specification.
Let us learn more about irrational numbers and the method to find their decimal expansions.
Did You Know?
In the 1870s, two mathematicians named Cantor and Dedekind stated that every real number is represented by a unique point on the number line and every point on the number line represents a unique real number.
Know Your Scientist


Irrationality of Square Roots of Non Perfect Square Numbers
We know that the decimal expansion of an irrational number is non-terminating and nonrepeating.
Take, for example, the irrational number √2 . Let us find its decimal expansion.

The decimal expansion of √2 is 1.41421…. It is clearly non-terminating and non-repeating.
So, √2 is an irrational number.
Decimal expansions of few more numbers are given below:
√7 = 2.64575…, √10 = 3.16227…., √65 = 8.06225 ….
In all cases, we found an irrational number.
It can be observed that 2, 7, 10 and 65 all are non perfect squares and their square roots are irrational numbers.
So, it can be concluded that the square roots of non perfect square numbers are irrational numbers.
Solved Examples
Easy
Example 1: Prove that √3 is an irrational number.
Solution:

The decimal expansion of √3 is 1.7320508…. It is clearly non-terminating and nonrepeating.
So, √3 is an irrational number.
Irrationality of nth Root of Numbers
Till now we have studied that the square root of a non-perfect square number is irrational.
But what about numbers in which the root is of an order greater than 2? Take, for example, the number 3√6 . In this number, the order of the root is 3. Since it is not possible to find the cube root of 6 as a terminating or repeating decimal number, 3√6 is an irrational number. We can conclude similarly about other numbers like 4√10 and 3√25 .
The irrationality of such numbers can be stated as follows:
The number n√a or a 1/n is irrational if it is not possible to represent a in the form bn, where b is a factor of a.
Know Your Scientist

Solved Examples
Example 1: Among the numbers √5 , √4 , 6√12 and √7 , which is/are irrational?
Solution:
We know that √a is an irrational number when ‘a’ is not a perfect square.
Among the given numbers, 4 is a perfect square. So, √4 is a rational number.
On the other hand, 5 and 7 are not perfect squares. Thus, √5 and √7 are irrational numbers.
6√12 is also irrational as 12 cannot be written in the form b6 where b is a factor of 12.
Representing Rational Numbers in Non-terminating Recurring Decimal Form Rational numbers have terminating decimal expansions, but they can be represented in the form of non-terminating recurring decimal numbers as well.
For example, 5/2 is a rational number as it is written in the form of p/q where q ≠ 0.
Now, 5/2 = 2.5 which is a terminating decimal number. 2.5 can also be written as 2.5000… or 2.50.
Thus, we get non-terminating recurring decimal form for the rational number 5/2.
Similarly, we can represent each rational number in non-terminating recurring decimal form.
Conversely, it can be said that every number in the non-terminating recurring decimal form is a rational number.
Solved Examples
Easy
Example 1: Represent the following rational numbers in non-terminating recurring decimal form.
a. 15/4
b. 2.007
c. 0.02
Solution:
a. The given number is 15/4 . It can be written in the non-terminating recurring decimal form as follows:
15/4 = 3.75 = 3.75000… = 3.750
b. The given number is 2.007. It can be written in the non-terminating recurring decimal form as follows:
2.007 = 2.007000… = 2.0070
c. The given number is 0.02. It can be written in the non-terminating recurring decimal form as follows:
0.02 = 0.02000… = 0.020
Conversion of Decimals into Rational Numbers
The Need for Converting Decimals into Fractions
In daily life, situations can arise wherein we have to separate a part of a whole for some purpose. Say, for example, a farmer wishes to give (0.3333…)th part of his three-hectare land to his eldest son.

Now, 0.3333… is not a terminating decimal. It is not possible to measure this decimal part of three hectares. However, if this non-terminating decimal is expressed as a fraction (i.e ,1/3) then the calculation becomes a lot easier and more accurate. It is now clear that the farmer wants to give his eldest son one-third of his land, i.e., one hectare out of the three hectares of land.
In this lesson, we will learn how to convert decimals into fractions.
Converting a Terminating Decimal into a Fraction
Solved Examples
Example 1: Express the number 2.25 in the form p/q
Solution:
Let x = 2.25
There are two digits after the decimal point; so, we can write:
x = 225/102 = 225/100
On simplification, we obtain:
x = 225/100 = 25×9/25×4 = 9/4
Thus, the number 2.25 can be written in the form p/q as 9/4 .
Converting a Non-Terminating Repeating Decimal into a Fraction
Solved Examples
Easy
Example 1: Express each of the following decimals as a fraction or a rational number.
1. 0.¯7
2. 0.¯29
Solution:
1. Let x = 0.¯7
⇒ x = 0.7777… … (1)
We have only one repeating digit after the decimal point. On multiplying equation 1 with
101 = 10, we get:
10x = 7.7777 … (2)
On subtracting equation 1 from equation 2, we get:
9x = 7
⇒ x = 7/9
∴ 0.¯7 = 7/9
2. Let x = 0.¯29
⇒ x = 0.292929… … (1)
We have two repeating digits after the decimal point. On multiplying equation 1 with
102 = 100, we get:
100x = 29.2929… … (2)
On subtracting equation 1 from equation 2, we get:
99x = 29
⇒ x = 29/99
∴ 0.¯29 = 29/99
Hard
Example 1: Find the rational forms of the following numbers.
1. 2.3—5961
2. 0.059
Solution:
1. Let x = 2.3—5961
x = 2.35961961… … (1)
On multiplying both sides of equation 1 with 100, we obtain:
100x = 235.961961961… … (2)
On multiplying both sides of equation 2 with 1000, we obtain:
100000x = 235961.961961961… … (3)
On subtracting equation 2 from equation 3, we obtain:
99900x = 235726
⇒ x = 235726/99900
⇒ x = 117863/49950
Thus, the rational form of 2.3—5961 is 117863/49950 .
2. Let x = 0.0¯59
x = 0.0595959… … (1)
On multiplying both sides of equation 1 with 10, we obtain:
10x = 0.595959… … (2)
On multiplying both sides of equation 2 with 100, we obtain:
1000x = 59.595959… … (3)
On subtracting equation 2 from equation 3, we obtain:
990x = 59
⇒ x = 59/990
Thus, the rational form of 0.0¯59 is 59/990 .
Finding Irrational Numbers between Given Rational Numbers
Real Numbers between Any Two Numbers
Consider the given number line.

This number line shows integers from −10 to 10. While there are clearly 19 integers between −10 and 10, the number of fractions between the two integers is infinite. So, we can say that there are infinite real numbers between any two numbers. Real numbers include both rational and irrational numbers. So we can say that there are infinite rational and irrational numbers between any two numbers.
In this lesson, we will learn to find irrational numbers between any two rational or irrational numbers.
Finding Irrational Numbers between Pairs of Rational Numbers
We know that between any two numbers, there are infinite rational and irrational numbers.
Let us learn to find irrational numbers between any two rational numbers. Here are the steps to do the same.
Step 1: Find the decimal representation (up to 2 or 3 places of decimal) of the two given rational numbers. Let those decimal representations be a and b, such that a < b.
Step 2: Choose the required non-terminating and non-repeating decimal numbers (i.e., irrational numbers) between a and b.
Similarly, we can find irrational numbers between other pairs of rational numbers.
Finding Irrational Numbers between Pairs of Rational Numbers
Solved Examples
Example 1: Find an irrational number between 0.12 and 0.15.
Solution:
Step 1: The rational numbers are already in the decimal form.
Let a = 0.12 and b = 0.15.
We can see that a < b.
Step 2:There is an infinite number of irrational numbers between a and b.
Clearly, the non-terminating and non-repeating number 0.12101001000… lies between 0.12 and 0.15. Hence, it is the required irrational number.
Example 1: Find five irrational numbers between 1/3 and 2/5 .
Solution: Step 1: The decimal expansion of 1/3 is 0.333…
The decimal expansion of 2/5 is 0.4 or 0.400.
We can see that 0.333 < 0.4.
Step 2: Five irrational numbers between 0.333 and 0.400 are listed below.
0.34560561562563…
0.3574744744474444…
0.369874562301…
0.3710110111011110…
0.39919293…
Representation of Rational Numbers on Number Line Using Successive Magnification
Introduction to Magnification
There are several things around us which are so small that they cannot be seen clearly with the naked eye; for example, the eyes of ants and small insects. These minute items can only be observed with the help of a lens that makes them appear bigger to the eye.

This process of making a thing seem bigger without actually changing its physical size is known as magnification. Generally, a magnifying glass is used for such enlargement.
Similarly, on the number line, there are infinite smaller numbers lying between any two numbers. These smaller numbers can be of two, three or more decimal places. To see or mark such numbers clearly, we use the process called successive magnification of the number line. Here, we use a virtual (imaginary) magnifying glass to enlarge the smaller divisions on the number line In this lesson, we will learn to represent rational numbers on the number line using the successive magnification method.
Successive Magnification of the Number Line
Watch this video to understand the need for the successive magnification of the number line.
Representing Numbers Using the Successive Magnification Method
Solved Examples
Medium
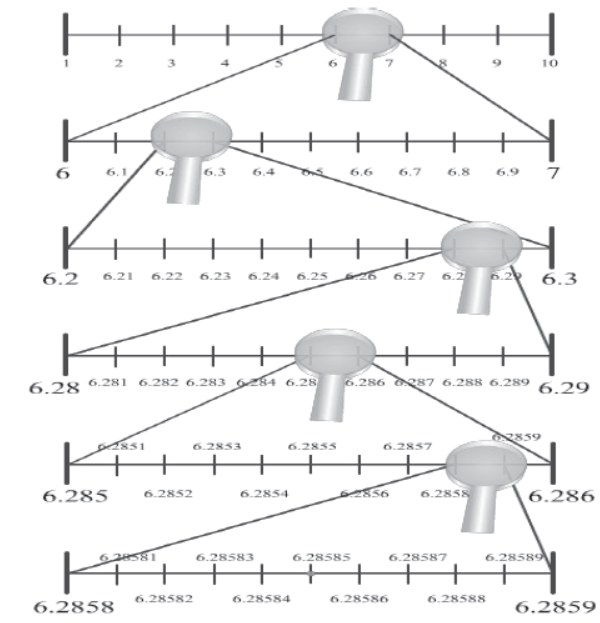
Example 1: Visualize 6.28¯5 on the number line, up to five decimal places.
Solution: 6.28¯5 can be expressed up to five decimal places as 6.28585. Here are the steps to visualize this number on the number line.
Step 1: 6.28585 lies between 6 and 7. Divide the number line between 6 and 7 into ten equal parts and magnify the distance between them.
Step 2: 6.28585 lies between 6.2 and 6.3. Divide the number line between 6.2 and 6.3 into ten equal parts and magnify the distance between them.
Step 3: 6.28585 lies between 6.28 and 6.29. Divide the number line between 6.28 and 6.29 into ten equal parts and magnify the distance between them.
Step 4: 6.28585 lies between 6.285 and 6.286. Divide the number line between 6.285 and 6.286 into ten equal parts and magnify the distance between them.
Step 5: 6.28585 lies between 6.2858 and 6.2859. Divide the distance between 6.2858 and 6.2859 into ten equal parts and magnify the distance between them. We can now mark 6.28585 on the number line.
The figures obtained at the end of each step are shown.
Representation of Irrational Numbers on Number Line
Square Root Spiral
Consider the given square root spiral.
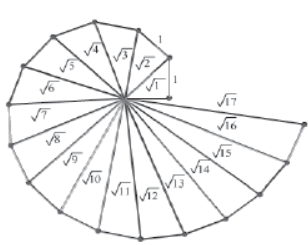
This spiral is obtained by geometrical representation of square roots of successive natural numbers 1, 2, 3…, and so on. We can construct this square root spiral if we know how to represent irrational numbers of the form √n on the number line, where n is any positive integer. Since irrational numbers are non-terminating and non-repeating, they are represented on the number line by a special method involving Pythagoras theorem.
In this lesson, we will learn to represent irrational numbers of the form √n on the number line.
Know Your Scientist

Representing Irrational Numbers of the Form √n on the Number Line
Concept Builder
Pythagoras theorem
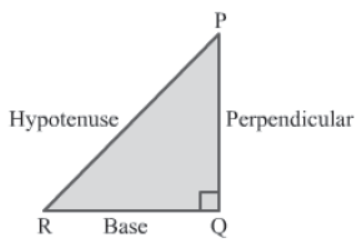
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Consider the following right-angled triangle PQR.
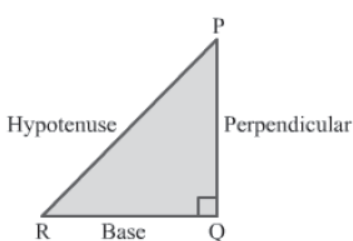
ΔPQR is right-angled at Q, i.e., ∠PQR = 90°. By Pythagoras theorem, we have:
Hypotenuse2 = Base2 + Perpendicular2
⇒ PR2 = RQ2 + PQ2
Solved Examples
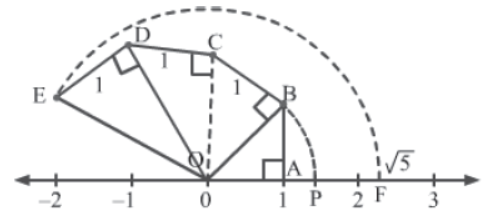
Example 1: Represent √5 on the number line.
Solution: Here are the steps to represent √5 on the number line.
Step 1: Draw a line and mark the integers −2, −1, 0, 1, 2, etc. on it, so that the distance between any two consecutive integers is one unit.
Step 2: Mark points O and A at 0 and 1 respectively. From A, draw a line segment AB of unit length and perpendicular to OA. Join O to B to get ΔOBA. Thus, by Pythagoras theorem, we have OB = √2
Step 3: From B, draw a line segment BC of unit length and perpendicular to OB. Join O to C to get ΔOCB. Thus, by Pythagoras theorem, we have OC = √3 .
Step 4: From C, draw a line segment CD of unit length and perpendicular to OC. Join O to D to get ΔODC. Thus, by Pythagoras theorem, we have OD = √4 .
Step 5: From D, draw a line segment DE of unit length and perpendicular to OD. Join O to E to get ΔOED. Thus, by Pythagoras theorem, we have OE = √5 .
Step 6: Now, taking O as the centre and OE as the radius, draw an arc that cuts the number line at point F. This point represents the irrational number √5 on the number line.
The figure for the construction is shown below.
Geometrical Representation of √n when (n − 1) is a Perfect Square
We have seen that to represent the square root of a number on the number line, the square root of its predecessor is used as the base of a right-angled triangle. So, if the number(n − 1) is a perfect square, then we can directly find its square root and use it to represent √n on the number line. Let us represent √5 on the number line using this method.
We have √5-1 = √4 = 2. So, we will consider a base of 2 units on the number line. To represent this base, mark points 0 and 2 as O and A respectively. From A, draw a perpendicular AB of unit length. Join O to B to get ΔOBA. Then, taking O as the centre and OB as the radius, draw an arc cutting the number line at point P. Point P represents the irrational number √5 on the number line.
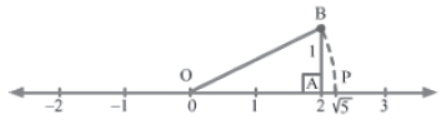
Let us verify our construction.
Using Pythagoras theorem in ΔOBA, we obtain:
OB2 = OA2 + AB2
⇒ OB2 = 22 + 12 = 4 + 1
⇒ OB = √5
∴OP = OB = √5 (∵ OP and OB are radii of the same arc)
In this way, we can represent other irrational numbers on the number line.
Geometrical Representation of √n when (n − 1) is a Perfect Square
Solved Examples
Example 1:Represent √17 on the number line and justify the construction.
Solution:
We know that 17 = 42 + 12. So, mark points 0 and 4 as O and A respectively. From A, draw a perpendicular AB of 1 unit. Join O to B to get ΔOBA. Then, take O as the centre and OB as the radius, and draw an arc that intersects the number line at point P. This point represents √17 on the number line. The construction is shown below.
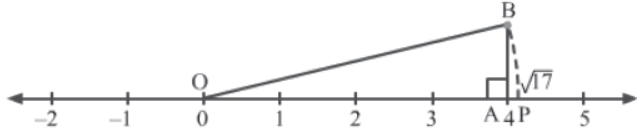
The construction can be verified as is shown.
We have OA = 4 units and AB = 1 unit. Using Pythagoras theorem in ΔOAB, we have:
OB2 = OA2 + AB2
⇒ OB2 = 42 + 12
⇒ OB2 = 16 + 1 = 17
⇒ OB = √17
∴OP = OB = √17 (∵ OP and OB are radii of the same arc)
Geometrical Representation of the Square Root of a Given Positive Real Number
Difficulty in Representing √n for a Positive Real Number on the Number Line
Suppose we have to represent √5.6 on the number line. We know that √5.6 is irrational since we cannot find a terminating or repetitive decimal number x such that x2 = 5.6.
We know how to represent √n , for any integer n, on the number line. For this, we locate √n-1 first and then √n . So, to locate √5.6 on the number line by the same method, we have to first locate √4.6 . Now, √4.6 is also an irrational number; to locate it on the number line, we have to first locate √3.6 , which is again an irrational number. It is clear that this method is not helpful in locating irrational numbers like √5.6 on the number line.
We use another method to represent such numbers on the number line. Go through this lesson to learn about the same.
Concept Builder
Square and square root
When a number is multiplied with itself, the obtained product is the square of the original number. Say, x is any number and x × x = y. In this case, the number y is the square of x. In exponential form, x × x is written as x2. This is called ‘square of x’, ‘x square’ or ‘x raised to the power 2’.
Now, we have assumed that x2 = y. So, x will be equal to the square root of y, which is represented as √y . Here, √ is the symbol of square root. Finding the square root of a number means representing the number as the product of another number multiplied with itself. It is the reverse of finding the square of a number. We have assumed y to beproduct of x × x; so, √y = x.
Locating √5.6 on the Number Line
Concept Builder
Pythagoras theorem
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Consider the following right-angled triangle PQR.
ΔPQR is right-angled at Q, i.e., ∠PQR = 90°. By Pythagoras theorem, we have:
Hypotenuse2 = Base2 + Perpendicular2
⇒ PR2 = RQ2 + PQ2
Know More
Square root
♦ The square root of every non-negative real number is a unique non-negative real number.
♦ The square root of 0 is 0.
♦ The square root of a negative real number is not a real number.
Solved Examples
Medium
Example 1:Represent √6.7 on the number line and justify the construction.
Solution: Here are the steps to locate √6.7 on the number line.
Step 1: Draw a line and mark a point A on it. Mark points B and C such that AB = 6.7 units and BC = 1 unit.
Step 2: Find the midpoint of AC and mark it as M. Taking M as the centre and MA as the radius, draw a semicircle.
Step 3: From B, draw a perpendicular to AC and let it meet the semicircle at point D. Taking B as the centre and BD as the radius, draw an arc that intersects the line at point E.
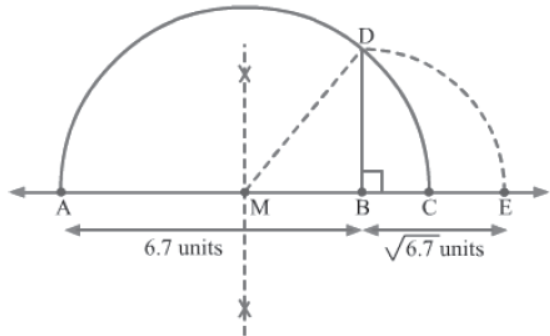
Now, the distance BE is √6.7 units.
Verification of construction:
We have AB = 6.7 units and BC = 1 unit
∴ AC = AB + BC = 6.7 units + 1 unit = 7.7 units
∴ MA = 1/2 AC = 1/2 X 7.7 units = 3.85 units
MB = AB − MA = 6.7 units − 3.85 units = 2.85 units
Also, MA = MD = 3.85 units (∵ MA and MD are the radii of the same circle)
On applying Pythagoras theorem in ΔMBD, we obtain:
BD2 = MD2 − MB2 = = 3.852 − 2.852 = 14.8225 − 8.1225 = 6.7
⇒ ∴ BD = √6.7 units
Hence, we get
BE = BD = √6.7 units (∵ BE and BD are the radii of the same circle)
Thus, our construction is justified.
Operations on Irrational Numbers
Mathematical Operations and Irrational Numbers
We have learnt to perform addition, subtraction, multiplication and division on integers, decimals and fractions. We can also perform these operations on irrational numbers of the form √n , where n is a positive real number.
Performing mathematical operations on irrational numbers is similar to performing these operations on algebraic expressions. For example, to add the algebraic expressions 2xy + 3y2 and x2y − 4xy, we first check and add the like terms and then write the unlike terms as they are. In our example, 2xy and −4xy are like terms as they have the common algebraic part xy.
So, (2xy + 3y2) + (x2y − 4xy) = (2xy − 4xy) + 3y2 + x2y = − 2xy + 3y2 + x2y
Irrational numbers are also categorized as like and unlike irrational numbers. We can add or subtract like irrational numbers only.
In this lesson, we will learn how to perform the four mathematical operations on irrational numbers.
Like terms: The terms or numbers whose irrational parts are the same are known as like terms. For example, 2/7√3 and 3/5√3 are like terms because the irrational parts in these
numbers are the same, i.e., √3 .
Unlike terms: The terms or numbers whose irrational parts are not the same are known as unlike terms. For example, 31/8√7 and 11/13√5 are unlike terms because the irrational parts in these numbers are different, i.e., √7 and √5 .
Sometimes, two numbers may appear to have different irrational parts, but on simplification they are found to be the same. For example, 5√2 and 3√8 seem to have different irrational parts, i.e., √2 and √8 . However, on simplifying 3√8 , we get 3√8 = 3(2√2) = 6√2 . Thus, we see that the two numbers have the same irrational part, i.e., √2 .
Arithmetic Operations between Rational and Irrational Numbers
We have learnt to perform operations between fractions and integers, decimals and whole numbers and different types of numbers. Now, let us try to perform the same between rational and irrational numbers.
Let us take the rational number 4 and the irrational number √7 . On applying the four operations on these numbers, we get 4 + √7,4 −√7 , 4 × √7 and 4/√7 Since √7
has a non-terminating and non-repeating decimal expansion, the decimal expansions of 4 + √7 , 4 − √7 , 4 × √7 and 4/√7 will also be non-terminating and nonrepeating.
Hence, these numbers will also be irrational.
So, we can conclude that:
♦ The sum or difference of a rational and an irrational number is always irrational.
♦ The product or quotient of a non-zero rational number and an irrational number is always irrational.
Solved Examples
Example 1:Check whether π + 8 and 4√3 -6/5 are irrational numbers or not.
Solution:
We know that π is an irrational number and 8 is a rational number. The sum of a rational and an irrational number is always irrational. Hence, π + 8 is an irrational number. It can be proved as follows:
π = 3.1415…
⇒ π + 8 = 3.1415… + 8 = 11.1415…
11.1415… is a non-terminating and non-repeating decimal number, so it is irrational.
We know that √3 is an irrational number and 4 is rational number. The product of a nonzero rational number and an irrational number is always irrational. Thus, 4√3 = 4 x √3
is an irrational number. Similarly, 4√3 – 6 is an irrational number as it is the difference between a rational and an irrational number. Finally, 4√3 -6/5 is an irrational number as it is the quotient of a non-zero rational number and an irrational number.
Performing Operations on Irrational Numbers
The decimal expansion of an irrational number is non-terminating and non-repeating. For this reason, unlike irrational terms cannot be added or subtracted.
Suppose √x and √y are two unlike irrational numbers. The arithmetic operations between them are shown as follows:
♦ Addition = √x + √y
♦ Subtraction = √x – √y or √y – √x
♦ Multiplication = √xx √y = √xxy = √xy
♦ Division = √x + √y = √x/√y = √x/y
Suppose a√x and b√x are two like irrational numbers. The arithmetic operations between them are shown as follows:
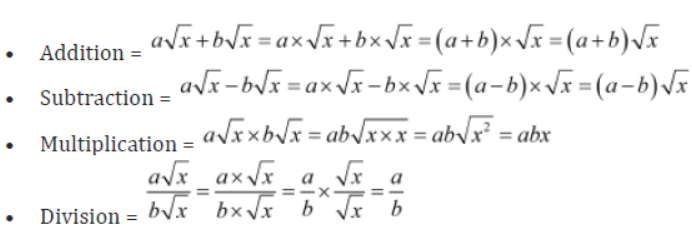
Solved Examples
Easy
Example 1:
1. Divide 8√21 by 2√7
2. Multiply 8√21 with 2√7
Solution:
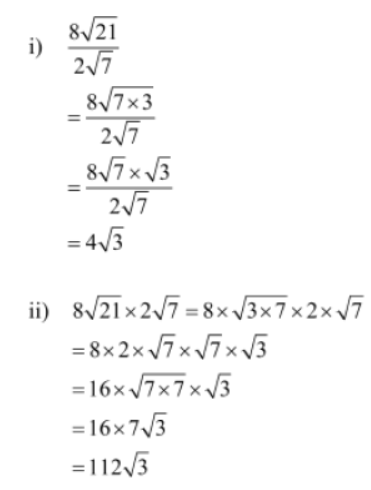
Example 2:
1. Prove that √24 + √54 = √150
♦ Subtract √125 from 2√5
Solution:
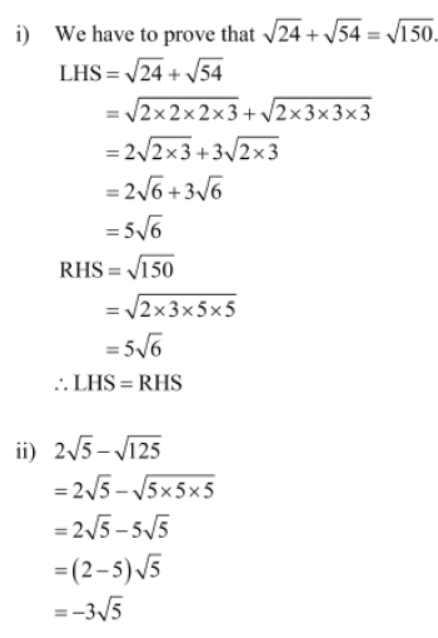
Example 1:Simplify √20 x 2√12/6√15
Solution:
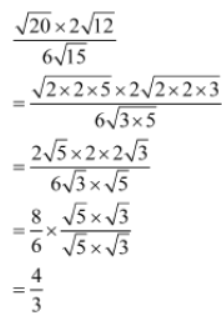
Concept Builder
There is an order in which calculations should be performed while simplifying an expression. This order of performing operations is called BODMAS, with each letter in this word standing for a particular operation.

While simplifying an expression, we should first remove the ‘brackets’. Next, weshould perform operations involving ‘of’, e.g., one fourth of 16, 20% of 100, etc. Then, we should carry out ‘division’, ‘multiplication’, ‘addition’ and ‘subtraction’, in that order.
All expressions are solved using the BODMAS rule. Take, for example, the expression
36 ÷ 12 + 7 × 2 − 7. We simplify this expression as follows:
36 ÷ 12 + 7 × 2 − 7
= 3 + 7 × 2 − 7 (Division)
= 3 + 14 − 7 (Multiplication)
= 17 − 7 (Addition)
= 10 (Subtraction)
Solved Examples
Easy
Example 1: Multiply (3√7 + 2√13) with √5 .
Solution:
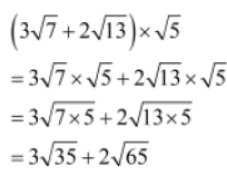
Example 2:Simplify 2√150 – 9/√3
Solution:
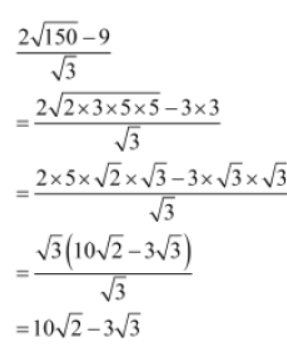
Medium
Example 1:Simplify (5+√7)(√7-2)+(3+√3)2
Solution:
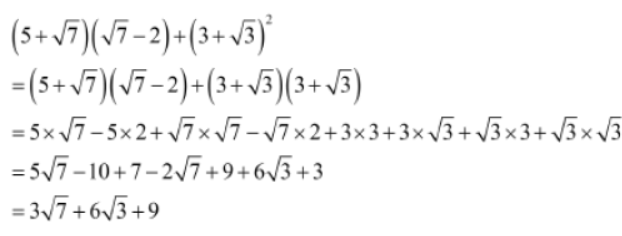
Example 2:Simplify (√486 +2) – (√27+√2)
Solution:
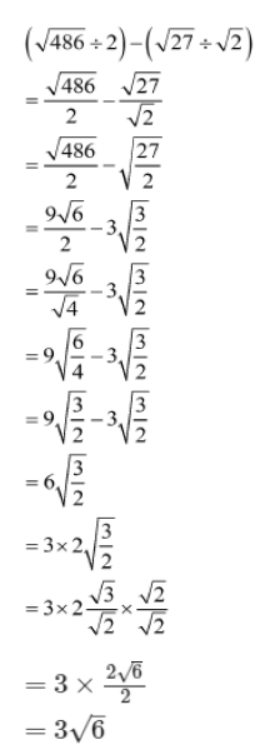
Closure Property of Irrational Numbers
Introduction to Closure Property
In order to study the closure property of irrational numbers, we first need to know the meaning of the term ‘closure property’. For this purpose, let us consider the two integers −5 and 8. The sum of these integers is 3 and the difference when 8 is subtracted from −5 is −13. You can see that the sum and the difference are both integers. What this tells us is that adding or subtracting two integers always gives an integer as the result. In other words, the sum or difference of integers is closed to be an integer. Thus, we can say that:integers are ‘closed’ with respect to addition and subtraction, or integers satisfy the closure property under addition and subtraction.
In this lesson, we will discuss the closure property of irrational numbers under different algebraic operations such as addition, subtraction, multiplication and division.
Know More
Division by 0:
Division means to divide the dividend (numerator) into as many equal parts as the divisor (denominator). For example, 4 ÷ 2 means that we need to divide the number 4 into two equal parts.
Division by 0 means dividing a whole into zero equal parts. There may be infinite number of ways in which we can divide that whole into unequal parts or zero equal parts. Thus, division by 0 is not defined.
Solved Examples
Example 1: State two irrational numbers whose:
1. sum is a rational number
2. sum is an irrational number
Solution:
1. Let us consider the two irrational numbers 2+√3 and 2-√3 .
The sum of these two numbers is found as follows:
(2+√3) + (2-√3)
= 2+√3 + 2-√3
= 4 (a rational number)
2. Let us consider the two irrational numbers √5 +3 and √5 – 3
The sum of these two numbers is found as follows:
(√5 +3) + (√5 – 3)
= √5 +3 + √5 – 3
= 2√3 (an irrational number )
Example 2: State two irrational numbers whose:1. difference is a rational number
2. difference is an irrational number
Solution:
1. Let us consider the two irrational numbers √2 + 3 and √2 -5
The difference between these two numbers is found as follows:
(√2 + 3) – (√2 – 5)
= √2 + 3 – √2 + 5
= 8 (a rational number)
2. Let us consider the two irrational numbers 2/5 -√6 and 8/5 – 2√6
The difference between these two numbers is found as follows:
(2/5 -√6) – (8/5 – 2√6)
= 2/5 – √6 – 8/5 + 2√6
= – 6/5 + √6 /(an irrational number)
Medium
Example 1: State two irrational numbers whose:
1. product is a rational number
2. product is an irrational number
Solution:
1. Let us consider the two irrational numbers 7+4√3 and 7-4√3
The product of these two numbers is found as follows:
(7+4√3)(7-4√3)
= 7(7-4√3) + 4√3 (7 – 4√3)
= 49 – 28√3 + 28√3 – (4√3 x 4√3)
= 49 -(4 x 4 x 3)
= 49-48
= 1 (a irrational number)
2. Let us consider the two irrational numbers 2+√3 and 5+√6
The product of these two numbers is found as follows:
(2+√3)(5+√6)
= 2(5+√6) + √3(5+√6)
= 10 + 2√6 + 5√3 + √18
= 10 + 2√6 + 5√3 + 3√2 (an irrational number)
Example 2: State two irrational numbers whose:
1. quotient is a rational number
2. quotient is an irrational number
Solution:
1. Let us consider the two irrational numbers 4+3√11 and 12+9√11 .
The quotient of these two numbers is found as follows:
4+3√11/12+9√11
= 4+3√11/3(4+3√11)
= 1/3 (a rational number)
2. Let us consider the two irrational numbers 3√33 and 6√11 .
The quotient of these two numbers is found as follows:
3√33/6√11
= 1/2 √33/11
= 1/2√3 (an irrational number)
3√33/6√11
= 1/2 √33/11
= 1/2 √3 (an irrational number)
Simplifying Expressions Involving Irrational Numbers Using Identities
Consider the expression (√2 + √3)(√2 – √3)
To solve this expression, we need to multiply each term in the first bracketed pair with each term in the second bracketed pair. Let us solve this expression.
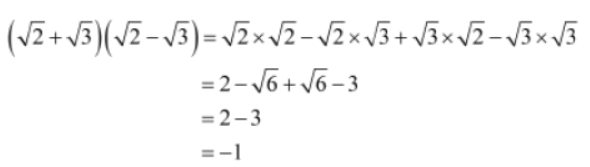
Is there an easier way to simplify the given expression? Yes, there is. We can solve such expressions using the identity: (√x + √y)(√x -√y) = x – y
On using this identity, we get the same value as obtained via the longer method.
(√2 + √3)(√2 – √3) = 2 – 3 = 1
There are other identities related to the square roots of positive real numbers. Let us first learn some of these identities and then we will apply them to solve problems.
Identities Related to the Square Roots of Positive Real Numbers
Here are some identities that help us solve problems involving irrational numbers.
If we consider x, y, p and q to be positive real numbers, then
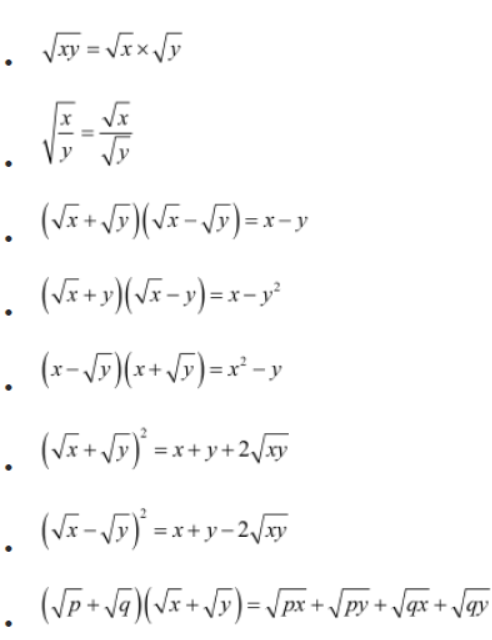
Concept Builder
Important algebraic identities
Here are some important algebraic identities that help us solve various types of problems.
♦ (a + b)2 = a2 + 2ab + b2
♦ (a − b)2 = a2 − 2ab + b2
♦ (a + b) (a − b) = a2 − b2
♦ (x + a) (x + b) = x2 + (a + b) x + ab
♦ (a + b)3 = a3 + b3 + 3ab(a + b)
♦ (a − b)3 = a3 − b3 − 3ab(a − b)
Solved Examples
Easy
Example 1: Simplify the following expressions using identities.
1. (√13 + √10)(√13 – √10)
2. (3 -√5)(3 + √5)
3. (√31 + 5)(√31 – 5)
4. (√11 – √17)2
5. (√6 + √11)2
6. (√2 + √3)(√7 + √23)
Solution:
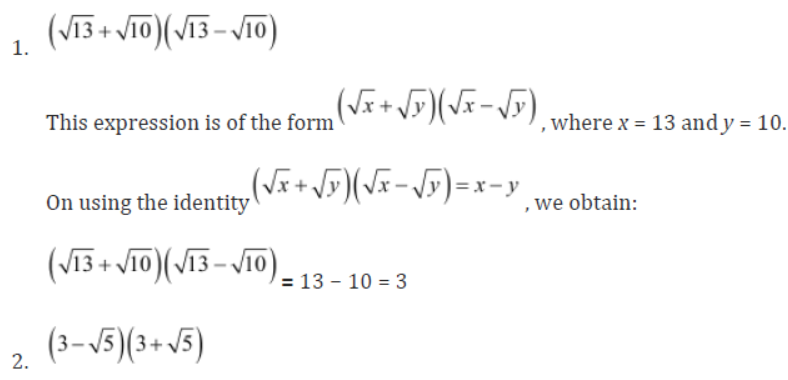

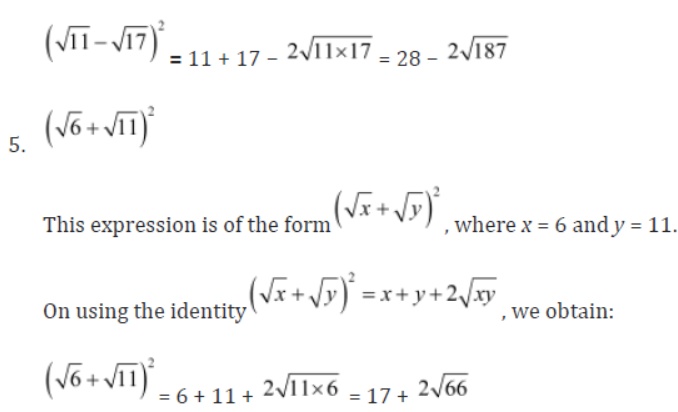
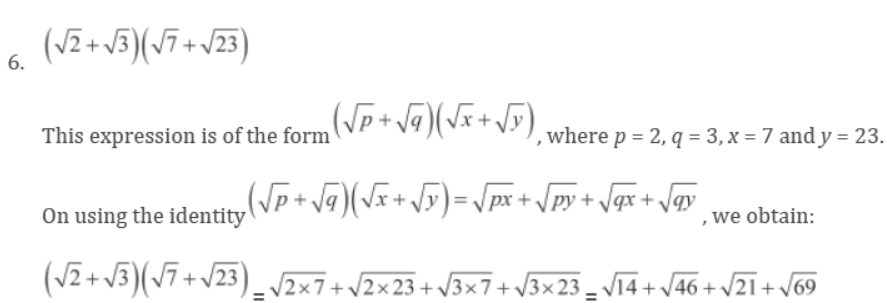
Example 1:The diagonals of a rhombus measure (4√5+8) units and (4√5-8) units.
Find the area of the rhombus.
Solution:

Example 2:Simplify the irrational number √6 – √20
Solution:

Example 1:Simplify the expression √(2+√45) – (3√5 -6)+√60
Solution:

Example 2: The length and breadth of a rectangle are (2+√6) units and (4+√3) units.
Solution:
Length (l) of the rectangle = (2+√6) units
Breadth (b) of the rectangle = (4+√3) units
Perimeter of the rectangle is given as:
2(l+b) units
= 2[(2+√6) + (4+√3)] units
= 2[6+√3 + √6] units
= (12 + 2√3 + 2√6 ) units
Area of the rectangle is given as:
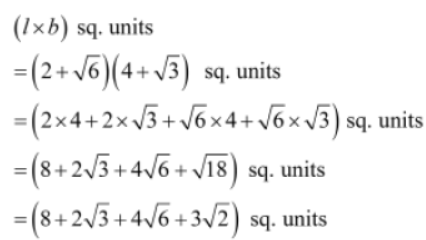
Rationalizing the Denominators
Rationalization
So far we have studied different operations on rational and irrational numbers, such as addition and subtraction. Now, what if we have to add two irrational fractions whose denominators are irrational numbers, say of the form √2 + 3 and √3+5 ? In such cases, we have to first rationalize the denominators, i.e., we have to make the denominators rational quantities (even if the numerators remain in the irrational form).
What does rationalization mean? Rationalization is the process in which an irrational fraction having a surd in the denominator is rewritten to obtain a rational number in the denominator. The surd may be a monomial or a binomial having a square root.
In this lesson, we will learn to:
♦ Rationalize the denominator of an irrational fraction
♦ Solve expressions using the rationalization method
Rationalizing the Denominator
Let us understand the method of rationalizing the denominator of an irrational fraction by taking the example of 1/√7 .
We know that √x x √x = x
∴ √7 x √7 = 7 , which is a rational number
So, we can write the expression 1/√7 as:
1/√7 x 1
= 1/√7 x √7/√7 (∴ √7/√7 = 1)
= √7/√7
Thus, we get a rational number as the denominator.
Let us now understand what is meant by ‘conjugate of a number’.
When a number is represented as the sum or difference of a rational number and an irrational number or two irrational numbers, the conjugate of that number just differs by the sign in between. For example, the conjugate of √2+3 is √2 – 3 and that of √2 + √3 is √2 – √3 or √3–√2. While solving irrational fractions having such denominators, we multiply and divide the fractions by the conjugates of the denominators.
Solving an Expression Using the Rationalization Method
Solved Examples
Example 1: Rationalize the denominator of 2/√3
Solution: We know that √3 x √3 = 3 , which is a rational number.
So, we multiply and divide 2/√3 by √3 .
2/√3 x √3/√3 = 2√3/3
Thus, we obtain a rational number as the denominator.
Example 2: Rationalize the denominator of 11√3 – 6/√3 + 2 .
Solution: To rationalize the denominator, we multiply and divide 11√3 – 6/√3 + 2 by the conjugate of √3 + 2
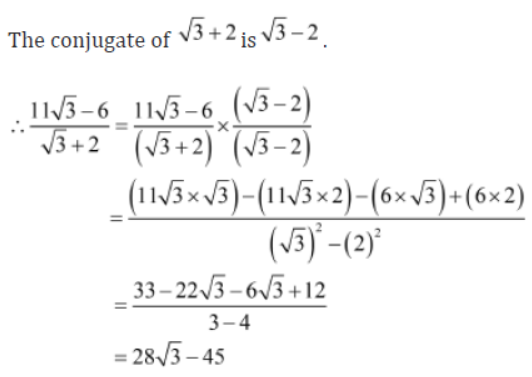
Example 1: Simplify the expression 6/2√3 – √6 + √6/√3+√2 – 4√3/√6 – √2.
Solution:
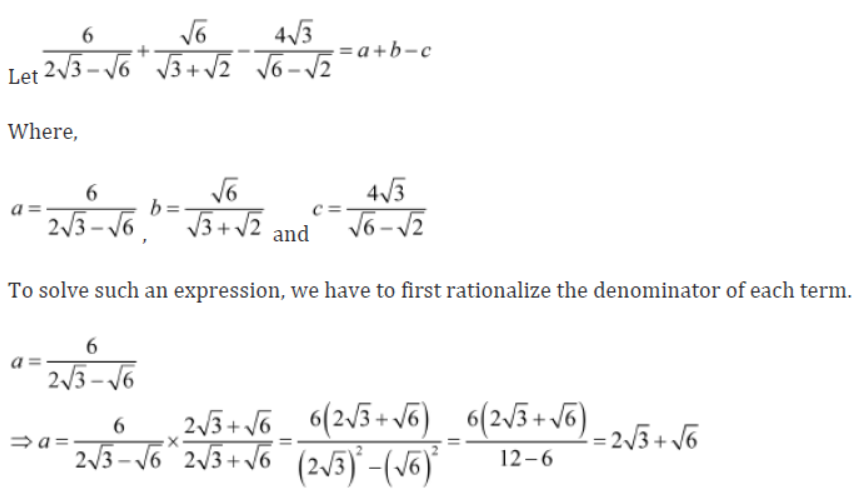

Example 2: Evaluate 15/√10 + √20 + √40 – √5 – √80
Solution:
Let us first simplify the denominator of the given expression.
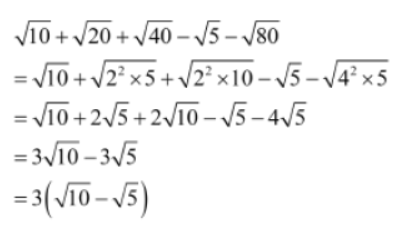
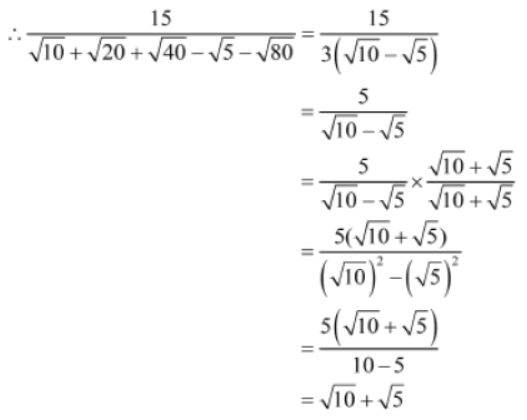
Example 1: Prove that 1/3-√8 – 1/√8 – √7 + 1/√7-√6 – 1/√6 – √5 + 1/√5 – 2 = 5
Solution:
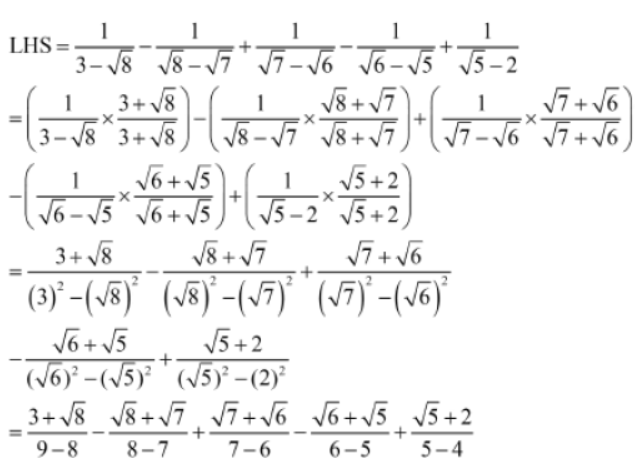
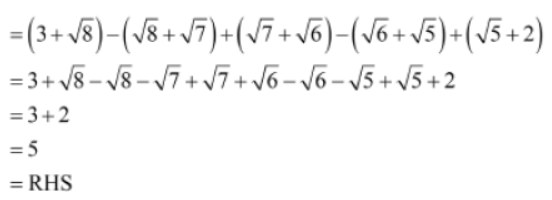
Example 2: If x = √3 + 1/2 , then find the value of 4×3 + 2×2 − 8x + 7.
Solution:
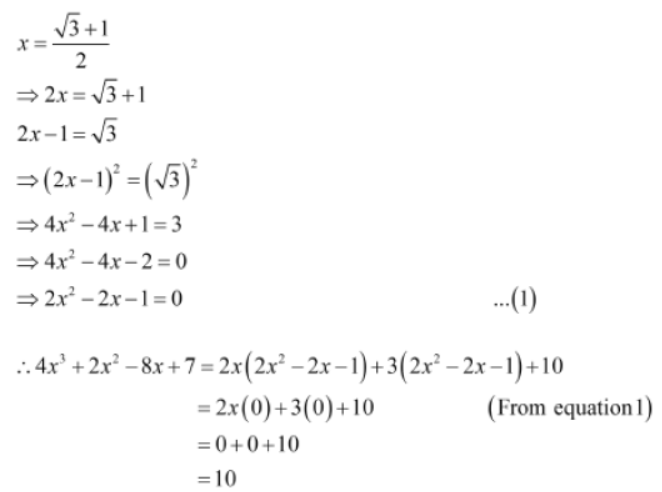
Laws of Rational Exponents of Real Numbers
Exponents or Indices
The term ‘exponent’ refers to the number of times a quantity is multiplied with itself. It is also called ‘index’ or ‘power’. The exponential form of any number is xy, where x is the base and y is the exponent. It is read as ‘yth power of x’ or ‘x raised to the power y’.
Till now, we have studied the laws of exponents for numbers having non-zero integers as the base and the integral exponent. For example, consider the expression 115 ÷ 113. It can be simplified using the law of exponents ap ÷ aq = a(p − q) as follows: 115 ÷ 113 = 11(5 − 3) = 112 But what about numbers whose base is any real number or whose exponent is any rational number?
Can we simplify them using the same laws? Go through this lesson to find out how to simplify such expressions.
Numbers with Fractional Indices
While studying about the exponents, we come across few numbers having fractional indices. For example, 1/83 , 1/162 , 1/814 etc.
Do you know what these numbers mean?
We know that the square root of a number is represented with the index 1/2 as well as with the symbol √.
For example, the square root of 16 can be represented as 16,1/2 and √16 .
Similarly, the square root of any real number a can be represented as 1/a2 and √a .
So, there are two ways to represent the square roots of numbers.
In the same manner, we can represent the cube root, fourth root, fifth root,…, nth root of a real number with the symbol √ as well as with fractional indices.
For example, the cube root of 8 can be represented as 3√8 and 8,1/3 . The fourth root of 81 can be represented as 4√81 and 8,1/4 .
Similarly, the nth root of a number can also be represented as n√a and a , 1/n
Solved Examples
Easy
Example 1: Find the values of the following index numbers.
i. 27,1/3
ii. 256,1/4
iii. 576,1/2
iv. 4096,1/2
Solution:
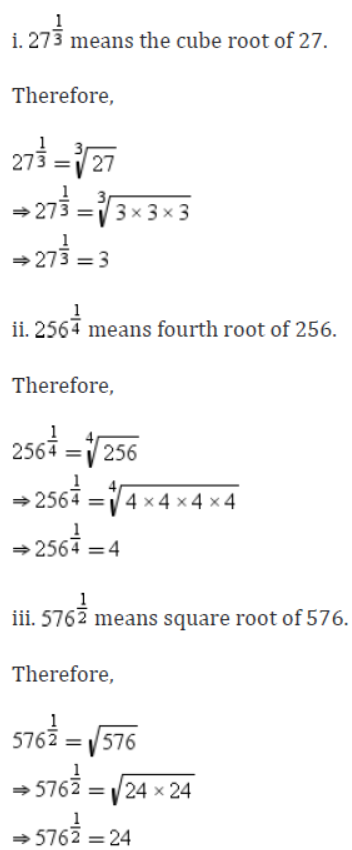
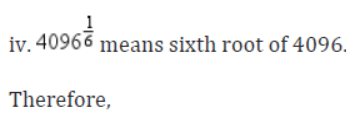
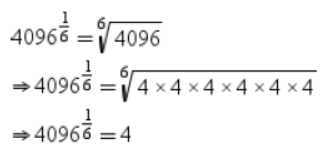
Laws of Exponents for Real Numbers
Consider two real numbers a and b and two rational numbers m and n. The laws of exponents involving these real bases and rational exponents can be written as follows:
Solved Examples
Example 1: Simplify the following expressions.
1. (27/125)2/3
2. 3√(512)-2
Solution:
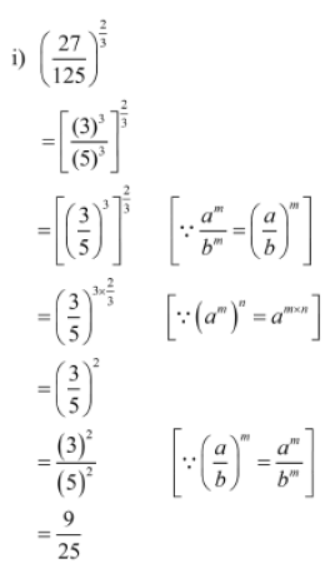
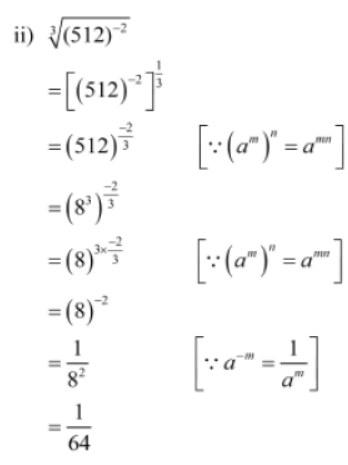
Example 2:Simplify the expression (√2/3)3/5 x (√1/7)3/5
Solution:
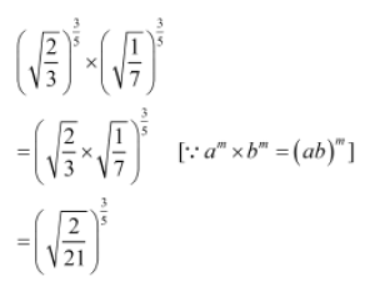
Example 3: Simplify 3√24 x 3√34
Solution:
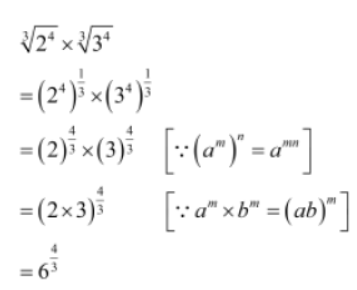
Example 1: Find the values of x and y in the expression 3x + 1 X 72y-1 = 189
Solution: It is given that 3x + 1 X 72y-1 = 189
⇒ 3x + 1 X 72y-1 = 3 x 3 x 3 x 7
⇒ 3x + 1 X 72y-1 = 33 x 71
On equating the exponents of 3 and 7 on both sides of the above equation, we get:
x + 1 = 3 and 2y − 1 = 1
⇒ x = 3 − 1 = 2 and 2y = 1 + 1 = 2
⇒ x = 2 and y = 1
Thus, the values of x and y are 2 and 1 respectively.
Example 1: Simplify the expression (243/32)-4/5 x [(625/81)-3/4 ÷ (25/4)-3/2] .
Solution:
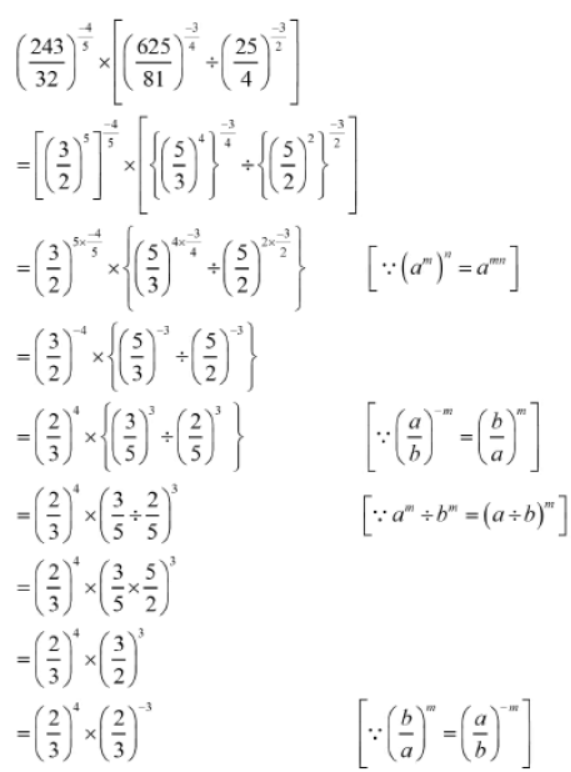

Example 2: Prove that xa(b-c)/xb(a-c) ÷ (xb/xa) = 1
Solution: