Please refer to Oscillations Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Oscillations Notes and Questions
- Periodic Motion: A motion which repeats itself over and over again after a regular interval of time.
- Oscillatory Motion: A motion in which a body moves back and forth repeatedly about a fixed point.
- Periodic function: A function that repeats its value at regular intervals of its argument is called periodic function. The following sine and cosine functions are periodic with period T.

These are called Harmonic Functions.
Note :- All Harmonic functions are periodic but all periodic functions are not harmonic.
One of the simplest periodic functions is given by
f(t) = A cos ωt [ω = 2π/T]
If the argument of this function ωt is increased by an integral multiple of 2π radians, the value of the function remains the same. The function f(t) is then periodic and its period, T is given by
T = 2π/ω
Thus the function f(t) is periodic with period T
f(t) = f(t +T)
Linear combination of sine and cosine functions
f(t) = A sin ωt + B cos ωt
A periodic function with same period T is given as
A = D cos ø and B = D sin ø
f(t) = D sin (ωt + ø)
D = √A2 + B2 and ø = tan -1 x/a
Simple Harmonic Motion (SHM): A particle is said to execute SHM if it moves to and fro about a mean position under the action of a restoring force which is directly proportional to its displacement from mean position and is always directed towards mean position.
Restoring Force ∝ Displacement
F ∝ x
F = -kx
Where ‘k’ is force constant.
Amplitude: Maximum displacement of oscillating particle from its mean position.
xMax = ± A
Time Period: Time taken to complete one oscillation.
Frequency: =1/T. Unit of frequency is Hertz (Hz).
1 Hz = 1s-1
Angular Frequency: ω = 2π /T2π
S.I unit ω = rad s-1
Phase:
1. The Phase of Vibrating particle at any instant gives the state of the particle as regards its position and the direction of motion at that instant.
It is denoted by ø.
2. Initial phase or epoch: The phase of particle corresponding to time t = 0.
It is denoted by ø.
Displacement in SHM :
x=A cos (ωt + ø0)
Where, x = Displacement,
A = Amplitude
ωt = Angular Frequency
ø0 = Initial Phase.
Case 1: When Particle is at mean position x = 0
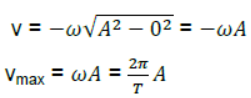
Case 2: When Particle is at extreme position x = ±A
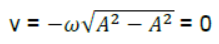
Acceleration
Case 3: When particle is at mean position x = 0, acceleration = – ω (0 ) = 0.
Case 4: When particle is at extreme position then x = A acceleration = – ω2A
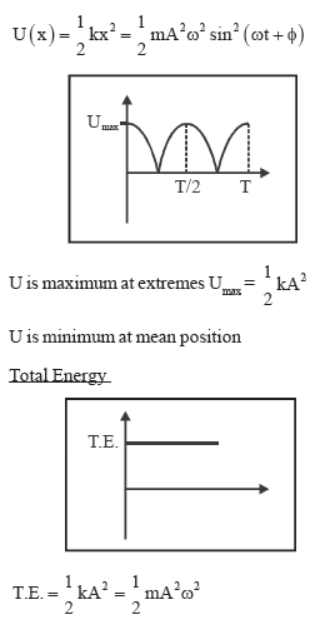
Formula Used :
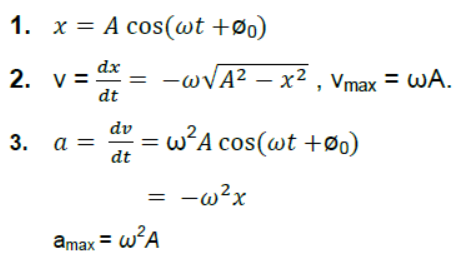

9. K.E. at displacement ‘y’ from the mean position
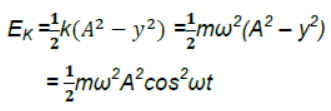
10. Total Energy at any point
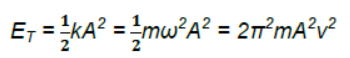
11. Spring Factor K = F/y
12. Period Of oscillation of a mass ‘m’ suspended from a massless spring of force constant ‘k’
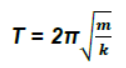
For two springs of spring factors k1 and k2 connected in parallel effective spring factor

13. For two springs connected in series, effective spring factor ‘k’ is given as
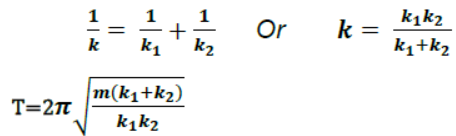
Note:- When length of a spring is made ‘n’ times its spring factor becomes 1/n times and hence time period increases √n times.
14. When spring is cut into ‘n’ equal pieces, spring factor of each part becomes ‘nk’.
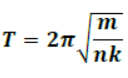
15. Oscillation of simple pendulum
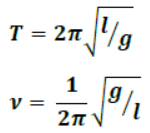
16. For a liquid of density ρ contained in a U-tube up to height ‘h’
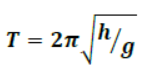
17. For a body dropped in a tunnel along the diameter of earth

18. Resonance: If the frequency of driving force is equal to the natural frequency of the oscillator itself, the amplitude of oscillation is very large then such oscillations are called resonant oscillations and phenomenon is called resonance.
INTRODUCTION
(1) A motion which repeats itself over and over again after a regular interval of time is called a periodic motion.
(2) Oscillatory or vibratory motion is that motion in which a body moves to and fro or back and forth repeatedly about a fixed point in a definite interval of time.
(3) Simple harmonic motion is a specific type of oscillatory motion, in which
(a) partical moves in one dimension,
(b) particle moves to and fro about a fixed mean position (where Fnet = 0),
(c) net force on the particle is always directed towards means position, and
(d) magnitude of net force is always proportional to the displacement of particle from the mean position at that instant.
So, Fnet = –kx
where, k is known as force constant
⇒ ma = – kx

where, ω is known as angular frequency.
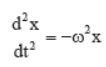
This equation is called as the differential equation of S.H.M.
The general expression for x(t) satisfying the above equation is :
x (t) = A sin (ωt + φ)
Some Important terms
1. Amplitude
The amplitude of particle executing S.H.M. is its maximum displacement on either side of the mean position.
A is the amplitude of the particle.
2. Time Period
Time period of a particle executing S.H.M. is the time taken to complete one cycle and is denoted by T.
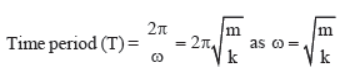
3. Frequency
The frequency of a particle executing S.H.M. is equal to the number of oscillations completed in one second.
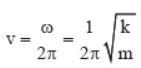
4. Phase
The phase of particle executing S.H.M. at any instant is its state as regard to its position and direction of motion at that instant. it is measured as argument (angle) of sine in the equation of S.H.M.
Phase = (ωt + φ)
At t = 0, phase = φ; the constant φ is called initial phase of the particle or phase constant.
Important Relations
1. Position
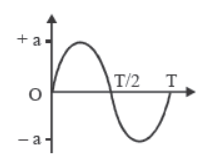
If mean position is at origin the position (X coordinate)
depends on time in general as :
x (t) = sin (ωt + φ)
♦ At mean position, x = 0
♦ At extremes, x = + A, –A
2. Velocity
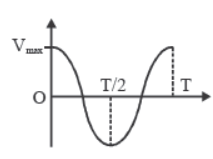
♦ At any time instant t, v (t) = A ω cos (ωt + φ)
♦ At any position x, v (x) = ± ω √A2 – x2
♦ Velocity is minimum at extremes because the particles is at rest.
i.e., v = 0 at extreme position.
♦ Velocity has maximum magnitude at mean position.
|v|max = ωA at mean position.
3. Acceleration
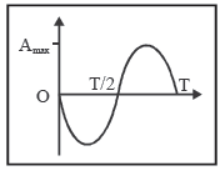
♦ At any instant t, a (t) = – ω2 A sin (ωt + φ)
♦ At any position x, a (x) = – ω2x
♦ Acceleration is always directed towards mean position.
♦ The magnitude of acceleration is minimum at mean position and maximum at extremes.
amin = 0 at mean position.
amax = ω2 A at extremes.
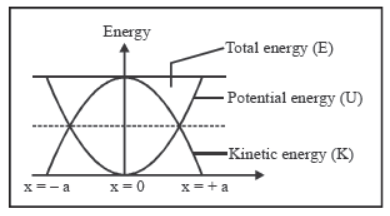
4. Energy
Kinetic energy

♦ Kmin = 0 at extemes.
Potential Energy
If potential energy is taken as zero at mean position, then at any position x,
and is constant at all time instant and at all positions.
Energy position graph
TIME PERIOD OF S.H.M.
To find whether a motion is S.H.M. or not and to find its time period, follow these steps :
(a) Locate the mean (equilibrium) position mathematically by balancing all the forces on it.
(b) Displace the particle by a displacement ‘x’ from the mean position in the probable direction of oscillation.
(c) Find the net force on it and check if it is towards mean position.
(d) Try to express net force as a proportional function of its displacement ‘x’.
♦ If step (c) and step (d) are proved then it is a simple harmonic motion.
(e) Find k from expression of net force (F = – kx) and find time period using T = 2π√m/k.
Oscillations of a Block Connected to a Spring
(a) Horizontal spring :
Let a block of mass m be placed on a smooth horizontal surface and rigidly connected to spring of force constant K whose other end is permanently fixed.
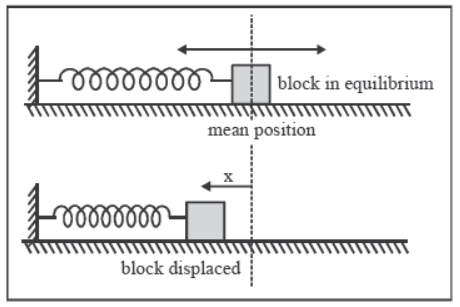
♦ Mean position : when spring is at its natural length.
♦ T = 2π√m/k.
(b) Vertical Spring :
If the spring is suspended vertically from a fixed point and carries the block at its other end as shown, the block will oscillate along the vertical line.
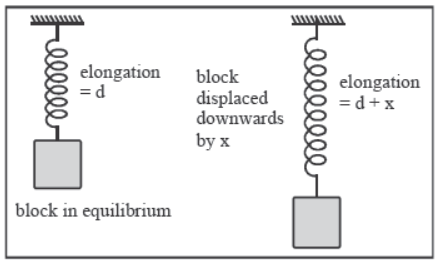
♦ Mean position : spring in elongated by d = mg/k
♦ Time period : T = 2π√m/k.
(c) Combination of springs :
1. Springs in series
When two springs of force constant K1 and K2 are connected in series as shown, they are equivalent to a single spring of force constant K which is given by
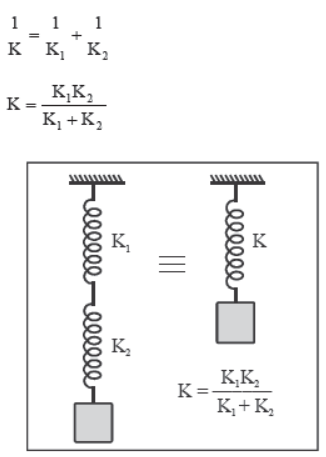
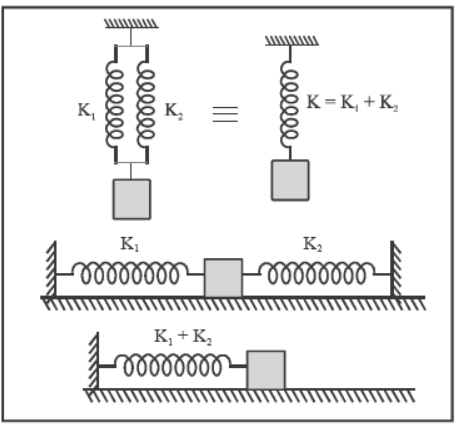
2. Springs in parallel
For a parallel combination as shown, the effective spring constant is K = K1 + K2
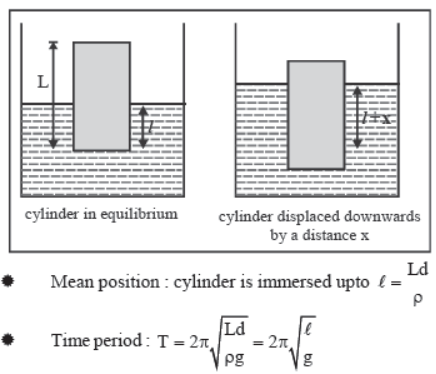
Oscillation of a Cylinder Floating in a liquid
Let a cylinder of mass m and density d be floating on the surface of a liquid of density p. The total length of cylinder is L.
Liquid Oscillating in a U–Tube
Consider a liquid column of mass m and density p in a Utube of area of cross section A.
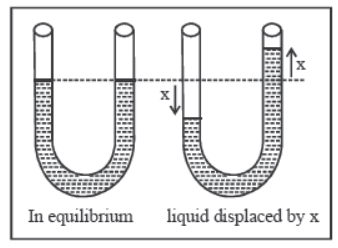
♦ Mean position : when height of liquid is same in both limbs.
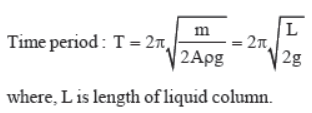
Body Oscillation in tunnel along any chord of earth
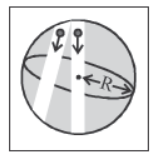
♦ Mean position : At the centre of the chord
Angular Oscillations
Instead of straight line motion, if a particle or centre of
mass of a body is oscillating on a small arc of circular
path then it is called angular S.H.M.
For angular S.H.M.,𝜏 = – kθ
♦ Iα = –kθ
♦ Time period, T = 2π√I/k
Simple Pendulum

♦ Second’s pendulum
Time period of second’s pendulum is 2s.
Length of second’s pendulum on earth surface ≅ 1m.
Physical Pendulum
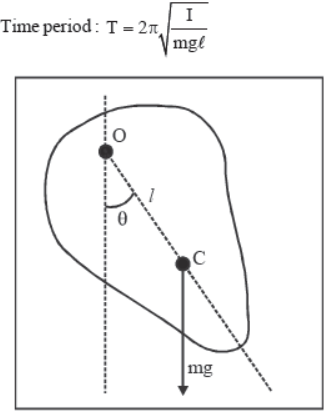
where, I is moment of inertia of object about point of suspension, and l is distance of centre of mass of object from point of suspension.
DAMPED AND FORCED OSCILLATIONS
1. Damped Oscillation :
(i) The oscillation of a body whose amplitude goes on decreasing with time is defined as damped oscillation.
(ii) In this oscillation the amplitude of oscillation decreases exponentially due to damping forces like frictional force, viscous force etc.
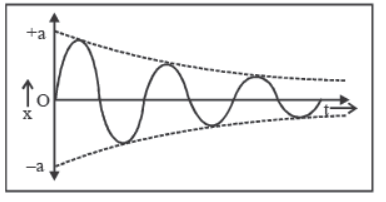
(iii) Due to decrease in amplitude the energy of the oscillator also goes on decreasing exponentially.
2. Forced Oscillation :
(i) The oscillation in which a body oscillates under the influence of an external periodic force are known as forced oscillation.
(ii) Resonance : When the frequency of external force is equal to the natural frequency of the oscillator, then this state is known as the state of resonance. And this
frequency is known as resonant frequency.
We hope the above Oscillations Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


