Students can read the important questions given below for Probability Class 12 Mathematics. All Probability Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Probability Class 12
Question. Two numbers are chosen from {1,2,3,4,5,6} one after the other without replacement. The probability that one of the smaller values is less than 4 is
(a) 4/5
(b) 1/15
(c) 1/5
(d) 14/15
Answer
A
Question. The probability of a student getting 1,2,3 division in an examination are 1/10, 3/5 and ¼ respectively. The probability that the student fails in the examination is
(a) 197/200
(b) 27/100
(c) 83/100
(d) None of these
Answer
B
Question. Let A and B are two events. If P(A)=0.2 p(B)=0.4, P(AᴜB)=0.6, then P(A/B) is equal to …
(a) 0.8
(b) 0.5
(c) 0.3
(d) 0
Answer
D
Question. A speaks truth in 75% cases and B speaks truth in 80% cases. The probability that they contradict each other in a statement is
(a) 7/20
(b) 13/20
(c) 3/5
(d) 2/5
Answer
A
Question. Let A and B be two events such that P(A)=0.6, P(B)=0.2 and P (A/B) =0.5, then P(A’/B’) equals…
(a) 1/10
(b) 3/10
(c) 3/8
(d) 6/7
Answer
C
Question. The probability that a leap year will have 53 Fridays or 53 Saturdays
(a) 2/7
(b) 3/7
(c) 4/7
(d) 1/7
Answer
B
Question. If A and B are independent events the P(A∩B) = ……
Answer
P(A).P(B)
Question. If a fair die is rolling. The events are E={1,3,6}, F={4,6}. Then the probability P(E/F) is…
(a) 1/6
(b) 1/3
(c) 1/2
(d) 2/3
Answer
C
Question. A person writes 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is
(a) 1/4
(b) 11/24
(c) 15/24
(d) 23/24
Answer
D
Very Short Answer Type
Question. The probabilities of A and B solving a problem independently are 1/3 and 1/4 respectively. If both of them try to solve the problem independently,what is the probability that the problem is solved?
Sol. 1- 2/3 x 3/4 = 1/2
Question. The probability that it will rain on any particular day is 50%. Find the probability that it rains only on first 4 days of the week.
Sol. (1/2)4(1/2)3 = (1/2)7
Question. A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?
Ans. Probability of defective watch from a lot 100 watches
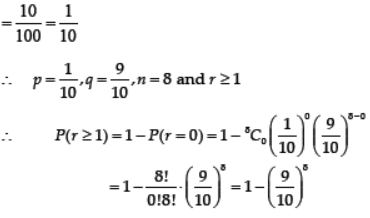
Question. A die is rolled twice. Find the probability of getting an odd number exactly once.
Answer :
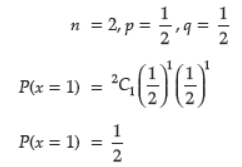
Question. Find the probability of getting a doublet twice when a pair of dice is thrown 4 times.
Answer :
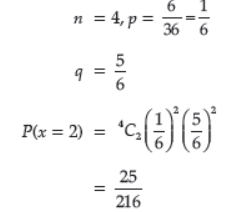
Short Answer Type Questions-I
Question. Given that E and F are events such that P(E) = 0.8, P(F) = 0.7, P (E Ç F) = 0.6. Find P (E|F) .
Answer :
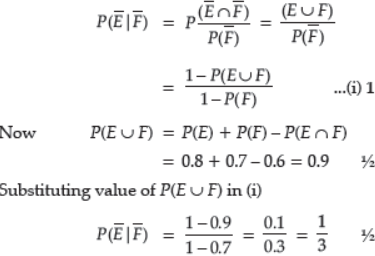
Question. Find [P(B/A) + P(A/B)], if P(A) = 3/10, P(B) = 2/5 and P(A È B) = 3/5.
Answer :

Question. Given two independent events A and B such that P(A¢) = 0.3 and P(B¢) = 0.6, find P(A¢Ç B¢).
Answer : P(A∩Ç B’) = P(A’) P(B’)
= (0.7)(0.4) = 0.28
Question. Three distinct numbers are chosen randomly from the first 50 natural numbers. Find the probability that all the three numbers are divisible by both 2 and 3.
Answer : Since there are only 8 numbers (in first 50 natural numbers) which are divisible by 6.
∴ favourable number of outcomes are 8C3.

Question. A speaks truth in 80% cases and B speaks truth in 90% cases. In what percentage of cases are they likely to agree with each other in stating the same fact?
Answer :


Question. A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.
Answer : Event A : Number obtained is even
B : Number obtained is red.

Question. If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P(A/B).
Answer : P(A) = 0.7Þ1 – P(A) = 0.7ÞP(A) = 0.3
P(A ÇB) = P(A) × P(B|A)= 0.3´ 0.5 = 0.15
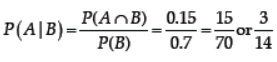
Question. One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red.
Answer : P (Red transferred and red drawn or black transferred and red drawn)

Question. If A and B are two independent events, prove that A’ and B are also independent.
Answer : P(A’ ∩ B) = P(B) – P(A ∩ B)
= P(B) – P(A) . P(B)
(∵ A and B are independent events)
= (1 – P(A)) P(B)
= P(A’) P(B) 1
Since, P(A’ ∩ B) = P(A’) P(B)
Therefore A’ and B are independent events.
Question. If P(A) = 0.6, P(B) = 0.5 and P(A|B) = 0.3, then find P(A È B).
Answer :

Question. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Answer : A : Getting a sum of 8, B : Red die resulted in no. < 4
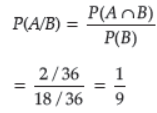
Question. If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’).
Answer : Required probability = P(A È B)
= P(A) + P(B) – P(A) · P(B)
= P(A) [1 – P(B)] + 1 – P(B’)
= P(A) P(B’) – P(B’) + 1
= 1 – P(B’) [1 – P(A’)]
= 1 – P(A’) P(B’)
Question. If P(A) = 2/5 , P(B) = 1/3 , P(A ∩ B) = 1/5 , then find P(A / B) .
Answer :

Question. A couple has 2 children. Find the probability that both are boys, if it is known that (i) one of them is a boy (ii) the older child is a boy.
Answer : Sample space = {B1B2, B1G2, G1B2, G1G2},
B1 and G1 are the older boy and girl respectively.
Let E1 = both the children are boys;
E2 = one of the children is a boy;
E3 = the older child is a boy
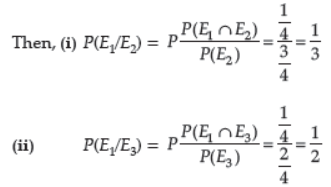
Question. A refrigerator box contains 2 milk chocolates and 4 dark chocolates. Two chocolates are drawn at random. Find the probability distribution of the number of milk chocolates. What is the most likely outcome?
Answer : Let X denote the number of milk chocolates drawn

Most likely outcome is getting one chocolate of each type
Question. The random variable X has a probability distribution P(X) of the following form, where ‘k’ is some number.
Answer : k + 2k + 3k = 1
⇒ k = 1/6
Question. Find the probability distribution of X, the number of heads in a simultaneous toss of two coins.
Answer :

Question. A die is thrown 6 times. If “getting on odd number” is a “success”, what is the probability of (i) 5 successes? (ii) atmost 5 successes ?
Answer : Let X: getting an odd number
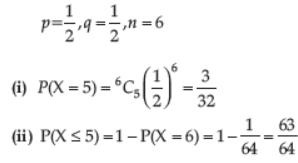
Question. A coin is tossed 5 times. What is the probability of getting (i) 3 heads, (ii) atmost 3 heads ?
Answer :

Short Answer Type Questions-II
Question. A and B throw a pair of dice alternately. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game by B.
Answer : Let x = event getting a total of 9, y = event getting a total of 7

Question. A bag contains (2n + 1) coins. It is known that (n – 1) of these coins have a head on both sides,whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed.
If the probability that the toss results in a head is 31/42 , determine the value of n.
Answer : No. of coins with head on both sides = (n – 1)
No. of fair coins = (n + 2)
Let event
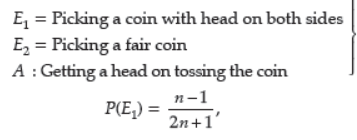
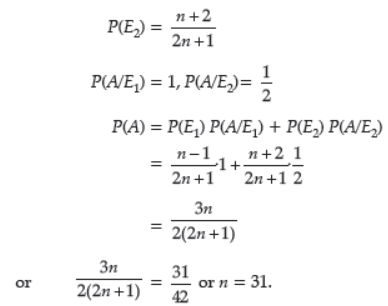
Question. A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3 .What is the probability that (i) the problem will be solved ? (ii) at most one of them solve the problem ?
Answer : Let
E be the event = A solves the problem
F be the event = B solves the problem
G be the event = C solves the problem
H be the event = D solves the problem


Question. Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively.
If both try to solve the problem, independently, then find the probability that
(i) the problem is solved
(ii) exactly one of them solves the problem
Answer : Let E1 : Problem solved by A
E2 : Problem solved by B

Question. In a shop X, 30 tins of ghee of type A and 40 tins of ghee of type B which look alike, are kept for sale. While in shop Y, similar 50 tins of ghee of type A and 60 tins of ghee of type B are there. One tin of ghee is purchased from one of the randomly selected shop and is found to be of type B. Find the probability that it is purchased from shop Y.
Answer : E1 : selecting shop X
E2 : selecting shop Y
A : purchased tin is of type B

Question. Suppose that 5 men out of 100 and 25 women out of 1000 are good orators. Assuming that there are equal number of men and women, find the probability of choosing a good orator.
Answer : Let M be an event of choosing a man and N be an event of choosing a women. A be an event of choosing a good orator.
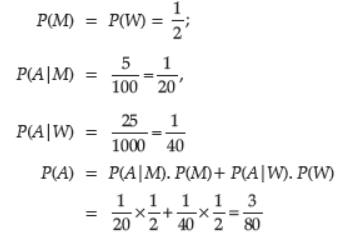
Question. There are three coins, one is a two headed coin (having head on both the faces), another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows head, what is probability that it was the two headed coin?
Answer : Let E1 = event of selecting a two headed coin
E2 = event of selecting a biased coin, which shows
75% times Head
E3 = event of selecting an unbiased coin.
A = event that tossed coin shows head.


Question. Suppose a girl throws a die. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4, 5 or 6, she tosses a coin once and notes whether a ‘head’ or ’tail’ is obtained.
If she obtained exactly one ‘tail’, what is the probability that she threw 3, 4, 5 or 6 with the die ?
Answer : E1 : She gets 1 or 2 on die.
E2 : She gets 3, 4, 5 or 6 on die.
A : She obtained exactly 1 tail

Question. Bag I contains 1 white, 2 black and 3 red balls; Bag II contains 2 white, 1 black and 1 red balls; Bag III contains 4 white, 3 black and 2 red balls. A bag is chosen at random and two balls are drawn from it with replacement. They happen to be one white and one red. What is the probability that they came from Bag III ?
Answer : Let E1 = Bag I is chosen, E2 = Bag II is chosen, E3 =
Bag III is chosen, A = The two balls drawn from the chosen bag are white and red.

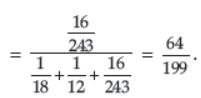
Question. Of the students in a school, it is known that 30% have 100% attendance and 70% students are irregular.
Previous year results report that 70% of all students who have 100% attendance attain A grade and 10%irregular students attain A grade in their annual examination. At the end of the year, one student is chosen at random from the school and he was found to have an A grade. What is the probability that the student has 100% attendance ?
Answer : Let E1 : Selecting a student with 100% attendance
E2 : Selecting a student who is not regular
A : selected student attains A grade.

Question. Often it is taken that a truthful person commands, more respect in the society. A man is known to speak the truth 4 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Answer : Let H1 be the event that 6 appears on throwing a die H2 be the event that 6 does not appear on throwing a die.
E be the event that he reports it is six.

Question. Bag A contains 3 red and 2 black balls, while bag B contains 2 red and 3 black balls. A ball drawn at random from bag A is transferred to bag B and then one ball is drawn at random from bag B. If this ball was found to be a red ball, find the probability that the ball drawn from bag A was red.
Answer : Let the events be
E1 : transferring a red ball from A to B
E2 : transferring a black ball from A to B
A : Getting a red ball from bag B

Question. Three persons A, B and C apply for a job of Manager in a Private company. Chance of their selection (A,B and C) are in the ratio 1 : 2 : 4. The probability that A, B and C can introduce changes to improve profits of company are 0·8, 0·5 and 0·3 respectively, if the changes does not take place, find the probability that it is due to the appointment of C.
Answer : Let the events be described as below :
A : No change takes place
E1 : Person A gets appointed
E2 : Person B gets appointed
E3 : Person C gets appointed
The chances of selection of A, B and C are in the ratio 1 : 2 : 4.
Hence,
P(E1) = 1/7 ; P(E2) = 2/7; P(E3) = 4/7
Probabilities of A, B and C introducing changes to improve profits of company are 0·8, 0·5 and 0·3 respectively.
Hence probability of no changes on appointment of A, B and C are 0·2, 0·5 and 0·7 respectively.
Hence,
P(A/E1) = 0·2 = 2/10
; P(A/E2) = 0·5 = 5/10 ;

Question. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise
bag B. It two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Answer : Let E1 = Selecting bag A
and E2 = Selecting bag B

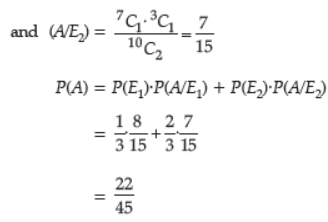
Question. Three machines E1, E2 and E3 in a certain factory producing electric bulbs, produce 50%,25% and 25% respectively, of the total daily output of electric bulbs. It is known that 4% of the bulbs produced by each of machines E1 and E2 are defective and that 5% of those produced by machine E3 are defective. If one bulb is picked up
at random from a day’s production, calculate the probability that it is defective.
Answer : Let A1 : Event that the bulb is produced by machine E1
A2 : Event that the bulb is produced by machine E2
A3 : Event that the bulb is produced by machine E3
A : Event that the picked up bulb is defective

Short Answer Type Questions
Question. 10% of the bulbs produced in a factory are of red colour and 2% are red and defective. If one bulb is picked up at random, determine the probability of its being defective if it is red.
Answer. Let A and B be the events that the bulb is red and defective, respectively.
P (A) = 10/100=1/10,
P((A∩B) =2/100=1/50
P (B | A) = P (A B)/P(A) = 1/5
Thus the probability of the picked up bulb of its being defective, if it is red, is 1/ 5.
Question. A family has two children. What is the probability that both the children are boys given that at least one of them is a boy ?
Answer. Let b stand for boy and g for girl. The sample space of the experiment is
S = {(b, b), (g, b), (b, g), (g, g)}
Let E and F denote the following events :
E : ‘both the children are boys’
F : ‘at least one of the child is a boy’
Then E = {(b,b)} and F = {(b,b), (g,b), (b,g)}
Now E ∩ F = {(b,b)}
Thus P(F) = 3/ 4 and P (E ∩ F )= 1/ 4
Therefore P(E|F) = P(E∩F)/ P(F)=1/3
Question. In a school, there are 1000 students, out of which 430 are girls. It is known that out of 430, 10% of the girls study in class XII. What is the probability that a student chosen randomly studies in Class XII given that the chosen student is a girl?
Answer. Let E denote the event that a student chosen randomly studies in Class XII and F be the event that the randomly chosen student is a girl. We have to find P (E|F) Now P(F) = 0.43 and P(E∩F)= 0.043 = (Why?)

Question. Ten cards numbered 1 to 10 are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3, what is the probability that it is an even number?
Answer. Let A be the event ‘the number on the card drawn is even’ and B be the event ‘the number on the card drawn is greater than 3’. We have to find P(A|B). Now, the sample space of the experiment is
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Then A = {2, 4, 6, 8, 10}, B = {4, 5, 6, 7, 8, 9, 10}
And A ∩ B = {4, 6, 8, 10}
Also P(A) = 5/10 , P(B) =7/10 and P(A∩ B)=4/10
Then
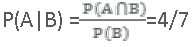
Question. A die is thrown twice and the sum of the numbers rising is noted to be 6. Calculate the is the conditional probability that the number 4 has arrived at least once?
Answer. If a dice is thrown twice, then the sample space obtained is:
S = {(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)}
From the given data, it is needed to find the Probability that 4 has appeared at least once, given the sum of nos. is observed to be 6
Assume that, F: Addition of numbers is 6 and take E: 4 has appeared at least once
So, that, we need to find P(E|F)
Finding P (E):
The probability of getting 4 atleast once is:
E = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6)}
Thus , P(E) = 11/ 36
Finding P (F):
The probability to get the addition of numbers is 6 is:
F = {(1, 5), (5, 1), (2, 4), (4, 2), (3, 3)}
Thus, P(F) = 5/ 36
Also, E ∩ F = {(2,4), (4,2)}
P(E ∩ F) = 2/36
Thus, P(E|F) = (P(E ∩ F) ) / (P (F) )
Now, substitute the probability values obtained= (2/36)/ (5/36)
Hence, Required probability is 2/5.
Question. A die is thrown three times. Events A and B are defined as below: A : 4 on the third throw B : 6 on the first and 5 on the second throw Find the probability of A given that B has already occurred.
Answer. The sample space has 216 outcomes.
Now A = {(1,1,4) (1,2,4) … (1,6,4) (2,1,4) (2,2,4) … (2,6,4)
(3,1,4) (3,2,4) … (3,6,4) (4,1,4) (4,2,4) …(4,6,4)
(5,1,4) (5,2,4) … (5,6,4) (6,1,4) (6,2,4) …(6,6,4)}
B = {(6,5,1), (6,5,2), (6,5,3), (6,5,4), (6,5,5), (6,5,6)}
and A ∩ B = {(6,5,4)}.
Now P(B) = 6/216 and P (A ∩ B) = 1/216

Question. A die is thrown twice and the sum of the numbers appearing is observed to be 6. What is the conditional probability that the number 4 has appeared at least once?
Answer. Let E be the event that ‘number 4 appears at least once’ and F be the event that ‘the sum of the numbers appearing is 6’.
Then, E = {(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (1,4), (2,4), (3,4), (5,4), (6,4)} and F = {(1,5), (2,4), (3,3), (4,2), (5,1)}
We have P(E) = 11/36 and P(F) = 5/36
Also E∩F = {(2,4), (4,2)}
Therefore P(E∩F)=2/36
Hence, the required probability
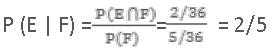
Question. An fair die is thrown double times. Assume that the event A is “odd number on the first throw” and B the event “odd number on the second throw”. Compare the independence of the events A and B.
Answer. Let us consider two independent events A and B, then P(A ∩ B) = P(A). P(B)
when an unbiased die is thrown twice
S = {(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)}
Let us describe two events as
A: odd number on the first throw
B: odd number on the second throw
To find P(A)
A = {(1, 1), (1, 2), (1, 3), …, (1, 6)
(3, 1), (3, 2), (3, 3), …, (3, 6)
(5, 1), (5, 2), (5, 3), …, (5, 6)}
Thus, P (A) = 18/36 = 1/2
To find P(B)
B = {(1, 1), (2, 1), (3, 1), …, (6, 1)
(1, 3), (2, 3), (3, 3), …, (6, 3)
(1, 5), (2, 5), (3, 5), …, (6, 5)}
Thus, P (B) = 18/36 = 1/2
A ∩ B = odd number on the first & second throw = { (1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5,
3), (5, 5)}
So, P(A ∩ B) = 9/36 = 1/ 4
Now, P(A). P(B) = (1/2) × (1/2) = 1/4
As P(A ∩ B) = P(A). P(B),
Hence, the two events A and B are independent events.
Question. Given that the events A and B are such that P(A) = 1/2, P (A ∪ B) = 3/5, and P(B) = p. Find p if they are
(i) mutually exclusive
(ii) independent
Answer. Given, P(A) = 1/2 ,
P (A ∪ B) = 3/5
and P(B) = p.
(1) For Mutually Exclusive
Given that, the sets A and B are mutually exclusive.
Thus, they do not have any common elements
Therefore, P(A ∩ B) = 0
We know that P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Substitute the formulas in the above-given formula, we get
3/5 = (1/2) + p – 0
Simplify the expression, we get
(3/5) – (1/2) = p
(6 − 5)/10 = p
1/10 = p
Therefore, p = 1/10
Hence, the value of p is 1/10, if they are mutually exclusive.
(ii) For Independent events:
If the two events A & B are independent,
we can write it as P(A ∩ B) = P(A) P(B)
Substitute the values,
= (1/2) × p
= p/2
Now, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Now, substitute the values in the formula,
(3/5) = (1/2)+ p – (p/2)
(3/2)– (1/2)= p – (p/2)
(6 − 5)/10 = p/2
1/10 = p/2
p= 2/10
P = 1/5
Thus, the value of p is 1/5, if they are independent.
Question. The probability of solving the specific problem independently by the persons’ A and B are 1/2 and 1/3 respectively. In case, if both the persons try to solve the problem independently, then calculate the probability that the problem is solved.
Answer. Given that, the two events say A and B are independent if P(A ∩ B) = P(A). P(B)
From the given data, we can observe that P(A) = 1/2 & P(B) = 1/3
The probability that the problem is solved = Probability that person A solves the problem or the person B solves the Problem
This can be written as:
= P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
If A and B are independent, then P(A ∩ B) = P(A). P(B)
Now, substitute the values,
= (1/2) × (1/3)
P(A ∩ B) = 1/6
Now, the probability of problem solved is written as
P(Problem is solved) = P(A) + P(B) – P(A ∩ B)
= (1/2) + (1/3) – (1/6)
= (3/6) + (2/6) – (1/6)
= 4/6
= 2/3
Hence, the probability of the problem solved is 2/3.
CASE STUDY :
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Based on the above information, answer the following
Question. What is the value of P(E1)?
a. 2/5
b. 1/3
c. 1
d. 3/5
Answer
D
Question. Value of P(E | E1) is
a. 1/3
b. 1
c. 2/3
d. 415
Answer
B
Question.

Equals
a. 11/15
b. 4/15
c. 1/5
d. 1
Answer
A
Question.

a. 1/3
b. 1/5
c. 1
d. 3/5
Answer
C
Question. What is the probability that the student knows the answer given that he answered it correctly?
a. 2/11
b. 5/3
c. 9/11
d. 13/3
Answer
C

