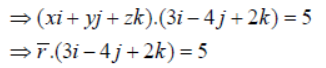Students can read the important questions given below for Three Dimensional Geometry Class 12 Mathematics. All Three Dimensional Geometry Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Three Dimensional Geometry Class 12
Question. If a line has direction ratios proportional to 2, -1, -2, then what are its direction cosines?
Answer: Given d.rs. are 2,-1,-2
If a,b,c are the d.rs. of a line then its d.cs. are

∴ The d.cs. of the given line is
Question. Find the equation of the plane through the line of intersection of

Answer: The equation of any plane through the line of intersection of the given
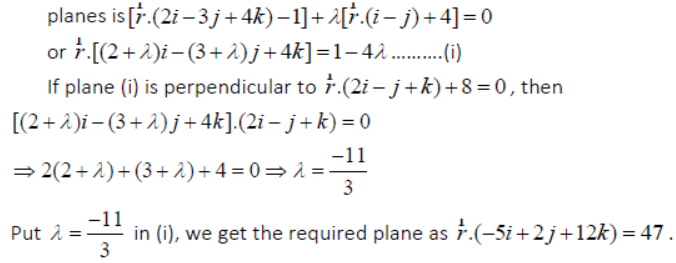
Question. Find the shortest distance between the lines


Answer: Given lines are


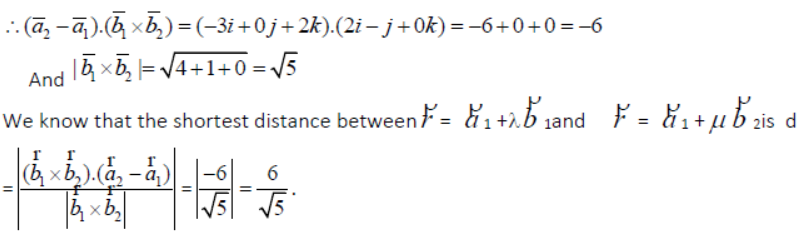
Question. Write the distances of the point (7, -2, 3) from XY, YZ and XZ-planes.
Answer: The distance of (7, -2, 3) from xy-plane is |3|= 3 units, from yz-plane is
|7|= 7 units and from zx-plane is |-2|= 2 units.
Question. If the equations of a line AB are 3-x/1 = y+2/-2 = z-5/4 . Write the direction ratios of a line parallel to AB.
Answer: Given line AB is 3-x/1 = y+2/-2 = z-5/4
It can be written as x-3/-1 = y+2/-2 = z-5/4
∴ d.rs. of any line parallel to AB are -1, -2, 4
Question. If a line makes angles 90o, 60o, 30o with the x,y and z axes respectively, find its direction cosines.
Answer:
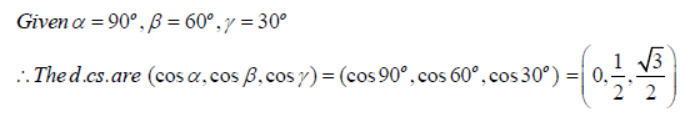
Question. Find the vector equation of the line passing through the points (-1, 0, 2) and (3, 4, 6).
Answer: Let A=(-1, 0, 2) and B= (3, 4, 6)
∴ The position vectors of A and B w.r.to the origin O are
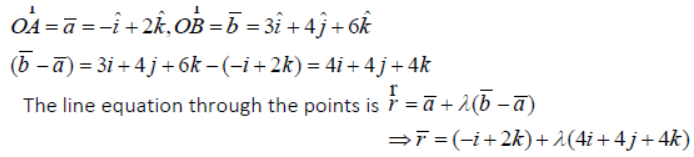
Question. Find the distance of the point (2, 3, 4) from x-axis.
Answer:

Question. Write the vector equation of a line given by x-5/3 = y+4/7 = z-6/2 .
Answer: Given line is x-5/3 = y+4/7 = z-6/2
A point on this line is (5, -4, 6) and has d.rs. proportional to 3, 7, 2.

Question. Find the image of the point (3, -2, 1) in the plane 3x-y+4z=2.
Answer: Let Q be the image of the point P(3, -2, 1) in the plane 3x-y+4z=2.
Then PQ is the normal to the plane. Therefore, d.rs. of PQ are proportional to 3, -1, 4.
Since PQ passes through P(3, -2, 1) and has d.rs. proportional to 3, -1, 4.

Question. Find the vector equation of the plane with intercepts 3, -4, 2 on x, y and Z – axis respectively.
Answer: The equation of the plane whose intercepts on the axes are a,b,c is

Question. Find the shortest distance between the lines whose vector equations are

Answer: Given lines are

Question. Find the foot of the perpendicular from the point P( 0, 2, 3) on the line x+3/5 = y-1/2 = z+4/3 . Also find the length of the perpendicular.
Answer: Let L be the foot of the perpendicular drawn from the point P(0, 2, 3) on the
given line x+3/5 = y-1/2 = z+4/3 = λ(say)
Any point on this line can be taken as (5λ −3,2λ +1,3λ − 4)
Let L be (5λ −3,2λ +1,3λ − 4) .
The d.rs. of the line PL are (5λ −3−0, 2λ +1− 2, 3λ − 4 −3) = (5λ −3,2λ −1, 3λ − 7)
The d.rs. of the given line are 5, 2, 3
But PL is perpendicular to the given line
∴ 5(5λ −3) + 2(2λ −1) + 3( 3λ −7) = 0 ⇒ λ =1
∴ Foot of the perpendicular L= (2, 3 -1).
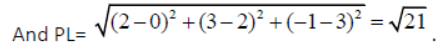
Question. Find the shortest distance between the lines x-3/1 = y-5/-2 = z-7/1 and x+1/7 = y+1/-6 = z+1/1 .
Answer: Given lines are

Question. Find the vector and Cartesian equations of the line through the point (5, 2, -4) And which is parallel to the vector 3î + 2 ĵ −8k̂ .
Answer: Let A= 1, 1, 1 (x y z ) =(5, 2, -4)
Then the position vector of A is a̅ = 5i + 2 j − 4k̂
Given vector b̅ = 3i + 2 j −8k
∴ The vector equation of the line is
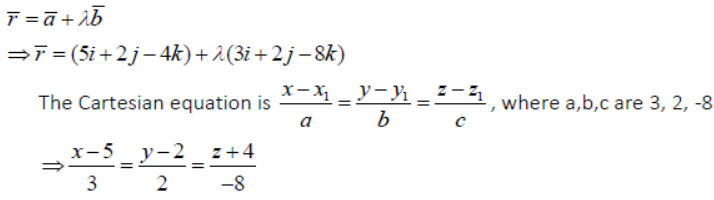
Question. Find the equation of the plane passing through the points P(1, 1, 0) , Q(1, 2, 1) and R(-2, 2, -1).
Answer: Given points are P(1, 1, 0) , Q(1, 2, 1) and R(-2, 2, -1).
Equation of a plane passing through three non collinear points

Question. Find the shortest distance between the lines x-1/2 = y-2/3 = z-3/4 and x-2/3 = y-4/4 = z-5/5.
Answer: The equations of the given lines are
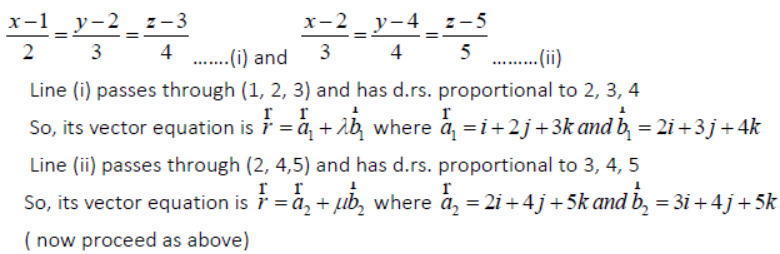
Question. Find a normal vector to the plane 2x-y+2z=5. Also find a unit vector normal to the plane.
Answer: Given plane is 2x-y+2z=5
The d.rs. of a vector normal to a plane ax+by+cz=d are a, b, c
∴ The d.rs. of a vector normal to 2x-y+2z=5 are 2, -1, 2
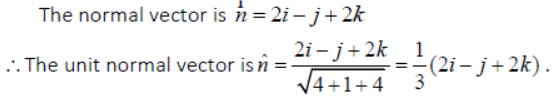
Question. Find the vector equations of the coordinate planes.
Answer: The vector equations of the coordinate planes are

Question. Find the equation of the plane passing through the point (1, -1, 2) having 2, 3, 2 as direction ratios of normal to the plane.
Answer: Given point is A=(1, -1, 2) and also given that the normal to the plane is

Question. Find the distance of the point (2, 1, 0) from the plane 2x+y+2z+5=0.
Answer: The distance from a point (x1,y1,z1) to the plane ax + by + cz + d = 0 is

Question. Find the points on the line x+2/3 = y+1/2 = z-3/2 at a distance of 5 units from from the point P(1, 3, 3).
Answer: Given line is x+2/3 = y+1/2 = z-3/2 = λ
Let Q be any point on the line , then Q = (3λ − 2,2λ −1,2λ + 3)
Given PQ=5 units
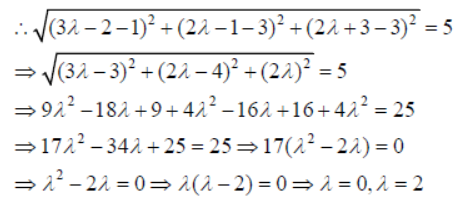
∴ The required points are (-2, -1, 3) and (4, 3, 7).
Question. Find the Cartesian equation of a plane whose vector equation is
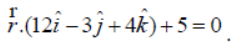
Answer:
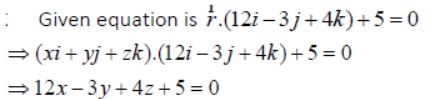
Question. Prove that the lines x+1/3 = y+3/5 = z+5/7 and x-2/1 = y-4/4 = z-6/7 are coplanar.
Also find the plane containing these two lines.
Answer: Given lines are x+1/3 = y+3/5 = z+5/7 and x-2/1 = y-4/4 = z-6/7


Question. Find the distance of the point (3, -5, 12) from x-axis.
Answer: The distance of P(x, y, z) from the x-axis
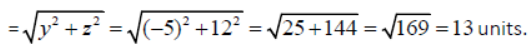
Question. Find the length and foot of the perpendicular from the point (7, 14, 5) to the plane 2x+4y-z =2.
Answer: Let Q be the foot of the perpendicular from the point P(7, 14, 5) on the plane 2x+4y-z=2.
Then PQ is the normal to the plane. Therefore, d.rs. of PQ are
proportional to 2, 4, -1. Since PQ passes through P(7, 14, 5) and has d.rs.
proportional to 2, 4, -1.

Question. Find the vector equation of the plane whose Cartesian form of equation is 3x-4y+2z=5.
Answer: Given plane is 3x-4y+2z=5