Students can read the important questions given below for Waves Class 11 Physics. All Waves Class 11 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 11 Physics Important Questions provided for all chapters to get better marks in examinations. Physics Question Bank Class 11 is available on our website for free download in PDF.
Important Questions of Waves Class 11
Question. Two astronauts on the surface of the moon cannot talk to each other why?
Answer : There is no atmosphere on the moon. Sound needs a material medium to travel. So they cannot talk each other directly.
Question. The length of a string tied to two rigid supports is 40 cm. What is the maximum wavelength of the stationary wave produced in it?
Answer : When the string vibrates in one segment,
L = λ/2
∴ λ = 2 L = 2 × 40 cm = 80 cm
Question. Intensities of two waves, which produce interference are 9 : 4. The ratio of maximum and minimum intensity is
Answer :

Question. Is it necessary for beat production that amplitudes of two waves should be exactly equal?
Answer : It is not at all necessary that the amplitudes of two waves producing beats should be equal. It is only when we wish to get zero sound at minima that the two amplitudes should be equal. However, the beats becomes more distinct as the amplitudes of two waves approach each other.
Question. What is the effect of pressure on the speed of sound in air? Justify your answer.
Answer : The speed of sound in a gas is given by,


pressure has no effect on the speed of sound in a gas for a given temperature.
Question. A wave of wavelength 2 m propagates through a medium. What is the phase difference between two particles on the line of propagation?
Given that the distance between the particles is 75 m.
Answer : The phase difference at any instant of time t, between two particles separated by distance Dx is given by

Question. Ocean waves hitting a beach are always found to be nearly normal to the shore. Why?
Answer : Ocean waves are transverse in nature and spread out in the form of concentric circles. When these waves reach the beach shore, their radius of curvature becomes so large that they can be treated as plane waves. Hence the ocean waves hit the beach nearly normal to the shore.
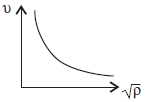
Question. Draw the graph between frequency and square root of density of a wire (keeping length, radius and tension constant).
Answer : The graph between frequency and square root of density of wire is
Question. A tuning fork A, marked 512 Hz, produces 5 beats per second, when sounded with another unmarked tuning fork B. If B is loaded with wax the number of beats is again 5 per second. What is the frequency of the tuning fork B when not loaded?
Answer : Here, vA = 512 Hz, vB = ?
As tuning fork is loaded with wax its frequency decreases hence, the actual frequency of tuning fork B is
vB = vA + 5 beats/s = 512 + 5 = 517 Hz
Question. Why is a loud sound heard at resonance?
Answer : At resonance, a compression falls on a compression and a rarefaction falls on a rarefaction. On account of this, the amplitude of the vibrating particles increases. Since the intensity of sound is directly proportional to the square of the amplitude of the vibrating particles, hence maximum sound is heard at resonance position.
Short Answer Type Questions :
Question. What do you understand by phase of a wave? How does the phase change with time and position?
Answer : The quantity (kx – ωt + Φ) appearing as the argument of sine function in general equation of wave is called the phase of the wave.
y(x, t) = a sin (kx – ωt + Φ).
The phase determines the displacement of the wave at any position and at any instant. Clearly, Φ is the phase at x = 0 and t = 0. Φ is called initial phase angle. By suitable choice of origin on the x-axis and the initial time, it is possible to have Φ = 0.
Question. A bat emits ultrasonic sound of frequency 1000 kHz in air. If this sound meets a water surface, what is the wavelength of
(a) the reflected sound,
(b) the transmitted sound? Speed of sound in air is 340 m s–1 and in water 1486 m s–1.
Answer :


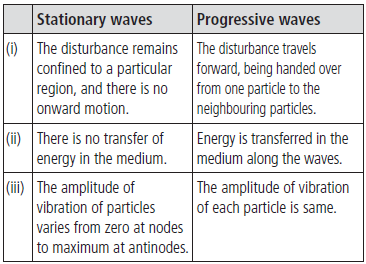
Question. What are the differences between stationary waves and progressive waves?
Answer :
Question. The velocity of sound, under STP conditions, equal 400 m/s. What will be the velocity when the
(i) pressure is changed to 2 atmospheric pressure without any change in temperature?
(ii) temperature is increased to 819 °C?
Answer :

Question. What do you mean by the independent behaviour of waves?
Answer : When a number of waves travel through the same region at the same time, each wave travels independently as if all other waves were absent.
This characteristic of wave is known as independent behaviour of waves. For example we can distinguish different sounds in a full orchestra.
Question. What are beats? Show that the number of beats produced per second is equal to the difference in frequencies.
Answer : Beats: Two wave trains of nearly same frequency and moving in the same direction, superpose and give rise to the phenomenon of beats.
Consider two harmonic waves of frequencies v1 and v2 (v1 being slightly greater than v2) and each of amplitude A travelling in a medium in the same direction. The displacements due to the two waves at a given observation point may be represented by
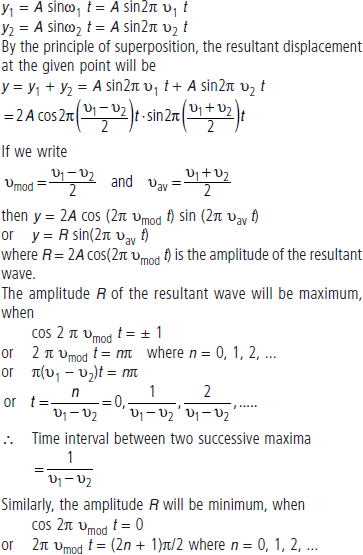
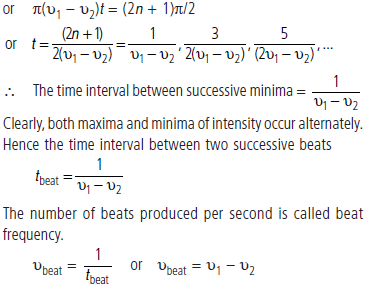
Question. A vessel is placed below a water tap. We can estimate the height of the water level reached in the vessel from a distance simply by listening to the sound. Why?
Answer : The frequency of sound produced in an air column is inversely proportional to the length of the air column. As level of water in the vessel increases, length of air column above it decreases. Hence, the frequency of the sound produced goes on increasing. The sound becomes shriller.
Question. (i) What kind of thermodynamical process occur in air, when a sound wave propagates through it?
(ii) The velocity of sound in a tube containing air at 27°C and pressure of 76 cm of Hg is 330 m s–1.
What will be its velocity, when pressure is increased to 152 cm of mercury and temperature is kept constant?
Answer : (i) When the sound wave travel through air adiabatic changes take place in the medium.
(ii) At a given temperature, the velocity of sound is independent of pressure, so velocity of sound in tube will remain 330 m s–1.
Question. Two periodic waves of intensities I1 and I2 pass through a region at the same time in the same direction.
What is the sum of the maximum and minimum intensities?
Answer : Other factors such as w and v remaining the same,
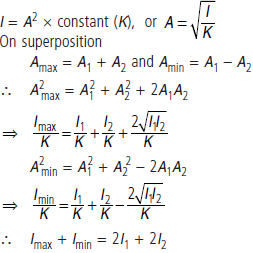
Question. If the phase difference between two sound waves of wavelength √ is 60°, what is the corresponding path difference?
Answer : Path difference for a given phase difference d is given
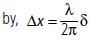

Question. Explain principle of superposition of waves in brief.
Answer : According to superposition of waves, when a medium is disturbed simultaneously by any number of waves, the instantaneous resultant displacement of the medium at every point and at every instant is the algebraic sum of the displacements of the medium due to individual waves in the absence of others.
Let y1, y2, y3……. be the displacements separately at a point in the medium, the resultant displacement y is given by,
y = y1 + y2 + y3 + ……..
Since each individual displacement is a function of time, so is the resultant displacement. The resultant displacement may be greater than the individual displacements, depending upon the phase relations amongst different displacements.
Question. A mechanical wave travels along a string is described by y(x, t) = 0.005 sin(3.0t – 80x) in which numerical constants are in SI units. Calculate
(a) Amplitude of displacement
(b) Amplitude of velocity
(c) Wavelength
(d) Amplitude of acceleration
(e) The time period
(f) Frequency of oscillation.
Answer :


Question. Calculate the speed of sound in a gas in which two waves of lengths 100 cm and 101 cm produce 24 beats in 6 second.
Answer :

Question. Discuss the effect of following factors on the speed of sound :
(a) Pressure
(b) Density
(c) Humidity
(d) Temperature
Answer : Effect on speed of sound due to :
(a) Pressure : There is no effect of pressure change on speed of sound as long as temperature remain constant.
(b) Density : The speed of sound is inversely proportional to the square root of density of medium.
(c) Humidity : Speed of sound increases with increases in humidity.
(d) Temperature : Speed of sound in a gas is directly proportional to square root of its temperature.
Question. Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1 and that of P wave is 8.0 km s–1. A seismograph records P and S waves from a earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line at what distance does the earthquake occur?
Answer : Speed of S wave = 4 km/s
Speed of P wave = 8 km/s
Let at d distance the earthquake occurs
∴ Time taken by S wave = d/4 s
Time taken by P wave = d/8 s
d/4 – d/8 = 4 min = 4 × 60 s ⇒ d = 1920 km.
Question. The frequencies of two tuning forks A and B are 250 Hz and 255 Hz respectively. Both are sounded together. How many beats will be heard in 5 s?
Answer : Here, vA = 250 Hz, vB = 255 Hz
Number of beats per second, v = vB – vA
= (255 – 250)Hz = 5 Hz
Number of beats heard in 5 s = vt = 5 × 5 = 25
Question. Even after breaking of one prong of tunning fork it produces a round of same frequency, then what is the use of having a tunning fork with two prongs?
Answer : Two prongs of a tunning fork set each other in resonant vibrations and help to maintain the vibrations for a longer time.
Question. The reference to a wave motion define the terms
(i) amplitude
(ii) wavelength
(iii) time period
(iv) frequency
Answer : (i) Amplitude: It is defined as the maximum displacement of an oscillating particle of the medium from the mean position. It is denoted by symbol A.
(ii) Wavelength : It is defined as the distance travelled by the wave during the time, the particle of the medium completes one oscillation about its mean position. It may also be defined as the distance between two consecutive points in the same phase of wave motion. It is denoted by symbol λ.
In case of transverse wave,
λ = distance between two consecutive crests or troughs.
In case of longitudinal waves,
λ = distance between two consecutive compressions or rarefactions.
(iii) Time period : It is defined as the time taken by a particle to complete one oscillation about its mean position. It is denoted by symbol T.
(iv) Frequency : is defined as the number of oscillations made by the particle in one second. It is denoted by symbol v. v = 1/T
Question. (i) How does the frequency of a tuning fork change, when the temperature is increased?
(ii) Is it necessary for beat production that amplitudes of two waves should be exactly equal?
Answer : (i) As the temperature increases, the length of the prong of the tunning fork increases and Young’s modulus changes. So, frequency of the tuning fork decreases.
(ii) It is not at all necessary that the amplitudes of two waves producing beats should be equal. It is only when we wish to get zero sound at minima that the two amplitudes should be equal. However, the beats becomes more distinct as the amplitudes of two waves approach each other.
Question. A plane progressive wave is given by y = 2cos6.284(330t – x). What is the period of the wave?
Answer : The given equation of a plane progressive wave is
y = 2cos6.284(330t – x)
= 2cos2π(330t – x) …(i)
The standard equation of a plane progressive wave is

Question. Why and how Laplace corrected Newton’s formula for velocity of sound in gases ?
Answer : Laplace pointed out that sound travels through a gas under adiabatic condition not under isothermal condition (as suggested by Newton). This is because of the following reasons :
(i) As sound travels through a gas, temperature rises in the regions of compressions and falls in the regions of rarefactions.
(ii) A gas is a poor conductor of heat.
(iii) The compressions and rarefactions are formed so rapidly that the heat generated in the regions of compressions does not get time to pass into the regions of rarefactions so as to equilise the temperature.
So when sound travels through a gas, the temperature does not remain constant. The pressure-volume variations are adiabatic. kadia is the adiabatic bulk modulus of the gas, then the formula for the speed of sound in the gas would be

This value is in close agreement with the experimental value. Hence, the Laplace correction is justified.
Long Answer Type Questions :
Question. For the wave described by
y(x, t) = 3.0 sin (36t + 0.018x + p/4) Plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs?
In which aspects does the oscillatory motion in travelling wave differ from one point to another : amplitude, frequency or phase?
Answer : The transverse harmonic wave is

For different values of t, we calculate y using equation (i). These values are tabulated below :
On plotting y versus t graph, we obtain a sinusoidal curve as shown in above figure.

Similar graphs are obtained for x = 2 cm and x = 4 cm. The oscillatory motion in travelling wave differs from one point to another only in terms of phase. Amplitude and frequency of oscillatory motion remain the same in all the three cases.
Question. A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36 t + 0.018 x + p/4) where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave? If it is travelling, what are the speed and direction of its propagation?
(b) What are its amplitude and frequency?
(c) What is the initial phase at the origin?
(d) What is the least distance between two successive crests in the wave?
Answer : The equation of the form

Question. The transverse displacement of a string (clamped at its two ends) is given by
y(x, t) = 0.06 sin (2p/3) × cos 120pt
where x, y are in m and t is in s. The length of the string is 1.5 m and its mass is 3.0 × 10–2 kg. Answer the following
(a) Does the function represent a travelling or a stationary wave?
(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What are the wavelength frequency and speed of propagation of each wave?
(c) Determine the tension in the string.
Answer :



