Please refer to Class 12 Mathematics Sample Paper Term 1 With Solutions Set E provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Term 1 Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
Term 1 Sample Paper for Class 12 Mathematics With Solutions Set E
1. The last two-digits of 220 is
(a) 76
(b) 20
(c) 36
(d) 16
Answer
A
2. The value of x in the set {0, 1, …… 77} satisfying 91x ≅ 42 (mod 78) is
(a) 0
(b) 5
(c) 73
(d) No solution
Answer
D
3. Let A2 – A + I = O. then A-1 is
(a) I – A
(b) A- I
(c) A+ I
(d) A
Answer
A
4.
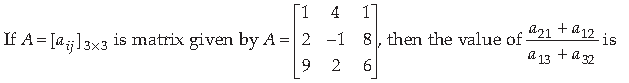
(a) 1
(b) 0
(c) 2
(d) 5
Answer
C
5. On the interval (0, 1) the function f (x) = x – [x] is
(a) increasing
(b) decreasing
(c) Both (a) and
(b) (d) None of these
Answer
A
6. A company finds its cost function to be C(x) = 1000 + 200x and its demand function to be p(x) = 10 – x, then the profit function P(x) is given by
(a) x2 + 190x + 1000
(b) – x2 – 190x + 1000
(c) – x2 + 190x + 1000
(d) – x2 – 190x – 1000
Answer
D
7. The percentage ratio between price of a commodity in the current year and that in the base year, is called
(a) Price relative
(b) Simple aggregate method
(c) Weighted aggregative
(d) None of these
Answer
A
8. An index number is used to measure
(a) changes in demand
(b) changes in price
(c) changes in a variable over time
(d) changes in quantity
Answer
C
9. For the given data å p1w = 9648 and å p0w = 8269 , where subscript 0 and 1 are used for base year and current year respectively, the index number by using weighted aggregates method is
(a) 116.67
(b) 109.52
(c) 121.24
(d) 115.42
Answer
A
10.
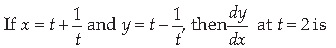
(a) 3/4
(b) 4/3
(c) 3/5
(d) 4/5
Answer
C
11.
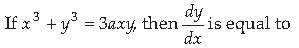

Answer
A
12.


Answer
A
13. A and B are invertible matrices of the same order such that | (AB)-1 | = 8, if |A| = 2, then |B| is
(a) 16
(b) 4
(c) 6
(d) 1/16
Answer
D
14. A runs 2 times as fast as B. If A gives B a start of 50 m, the goal on the race course be so that A and B reach it at the same time
(a) 80 m
(b) 40 m
(c) 50 m
(d) 100 m
Answer
D
15. A bag contains 2 black and 1 green balls. One ball is draw at random and then put back in the box after noting its colour. The process repeated again. Let X denotes the number of green balls recorded in the two draws, then range of X is
(a) {0, 1}
(b) {1, 2}
(c) {0, 1, 2}
(d) None of these
Answer
C
16. In a meeting, 60% of the members favour a certain proposal, 40% being opposite. A member is selected at random and let X = 0, if he opposed and X = 1, if he is in favour. Then, Var(x) is
(a) 1/25
(b) 4/25
(c) 7/25
(d) 6/25
Answer
D
17. The standard deviation of a poisson variate is 3.The probability that X = 2 is (given e-3 = 0.0498)
(a) 0.2341
(b) 0.1125
(c) 0.2241
(d) 0.567
Answer
C
18. A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then the probability that there will be atleast one defective watch is

Answer
C
19. The solution set of the inequality 2y – 3 < y + 1 ≤ 2y + 5 is
(a) (-4, 4]
(b) [-4, 4)
(c) [-4, 4]
(d) [4, – 4)
Answer
B
20. A 20L mixture contains milk and water in the ratio of 3 : 1. The quantity of milk to be added in the mixture such that the ratio of milk and water in the mixture becomes 4 : 1, is
(a) 6 L
(b) 5 L
(c) 4 L
(d) 7 L
Answer
B
Section B
21. The non-negative remainder when 910 is divided by 11 is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
22. The value of x satisfying (x – 1)(x + 2) ≅ (x – 2)(x + 7) (mod n), if nis odd, is
(a) 0
(b) 3
(c) 5
(d) 4
Answer
B
23. Suppose A is square matrix such that A3 = 1 , then (A + I) 3 + (A – I) 3 – A 6 equal to
(a) I
(b) 2 I
(c) A
(d) 3A
Answer
B
24.
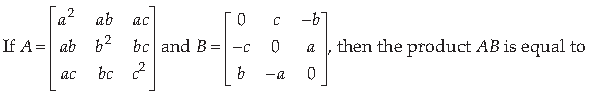
(a) 0
(b) A
(c) B
(d) I
Answer
A
25. The point on the curve x2 + y2 – 2x – 3 = 0 at which tangent is parallel to X-axis are
(a) (1, ±2)
(b) (±1, 2)
(c) (±1, ±2)
(d) (±2, ±1)
Answer
A
26. The price relative of a commodities in 2017 compared to 2015 is 200. If the cost of goods was ₹ 25 per kg in 2015, then cost of commodities in 2017, is
(a) ₹ 50
(b) ₹ 40
(c) ₹ 60
(d) ₹ 55
Answer
A
27. For the given data ∑p0 q0 = 324 , ∑ p1q1 = 392, ∑p0q1 = 336 and ∑p1q0 = 365, where subscript 0 and 1 are used for base year and current year respectively. The Laspeyre’s price index is
(a) 119.75
(b) 112.65
(c) 124.39
(d) 127.09
Answer
B
28. Bowley’s index number is based on
(a) GM of Laspeyre’s and Paasche’s index
(b) AM of Laspeyre’s and Paasche’s index
(c) HM of Laspeyre’s and Paasche’s index
(d) None of the above
Answer
B
29. To find the index number by Edgeworth’s method, we use the formula

Answer
A
30.
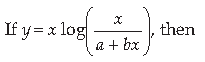

Answer
C
31.
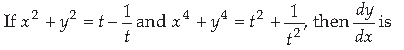

Answer
C
32. For the system of equations 5x – y + 4z = 5, 2x + 3y + 5z = 2 and 5x – 2y + 6z = – 1, then values of x, y and z are respectively
(a) 3, 2 and 2
(b) 3, 2 and -2
(c) 3, -2 and 2
(d) 1, 2 and 1
Answer
B
33.
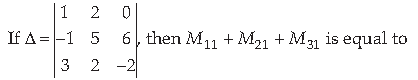
(a) 14
(b) -14
(c) 4
(d) -4
Answer
B
34. In 600 m race, A defeats B by 60 m. In 500 m race, B defeats C by 50 m. In 400 m race, A will defeats C by
(a) 76 m
(b) 18 m
(c) 27 m
(d) 10 m
Answer
A
35. The probability distribution of a discrete random variable X is given as under

If A = 3 and E(X) = 2.94, then variance of X is
(a) 10.41
(b) 9.41
(c) 11.41
(d) 8.41
Answer
A
36. From a lot of 15 bulbs which include 5 defectives, a sample of 2 bulbs is drawn at random (without replacement). The probability distribution of the number of defective bulbs is
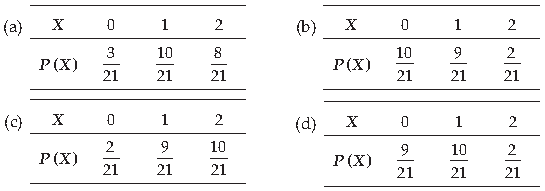
Answer
D
37. Between the hours 3 and 5 pm, the average number of phone calls per minute coming into the switchboard of a company is 2. The probability that during one particular minute there will be no phone call at all is (given e-2 = 0.13435)
(a) 0.12536
(b) 0.86565
(c) 0.13435
(d) None of these
Answer
C
38. A box contains 400 tickets each bearing one of the numbers from 1 to 400. 40 tickets are drawn successively with replacement from the box. The probability that at most 3 tickets bear numbers divisible by 40 is
(a) 0.8876
(b) 0.8976
(c) 0.9936
(d) 0.9763
Answer
C
39. A boatman rows 1 km in 5 min along the stream and 6 km in 1 h against the stream. The speed of the stream is
(a) 3 km/h
(b) 6 km/h
(c) 10 km/h
(d) 12 km/h
Answer
A
40. A shopkeeper purchases 40 kg of sugar at the rate of ₹ 35 per kg and 50 kg of sugar at the rate of ₹ 40 per kg. He mixed these two types of sugar. He sell the mixture to make a 20% profit in the transaction at the price of
(a) ₹ 45.33 per kg
(b) ₹ 47.67 per kg
(c) ₹ 35.39 per kg
(d) ₹ 37.30 per kg
Answer
A
Section C
41. The price and quantities of certain commodities are shown in the following table
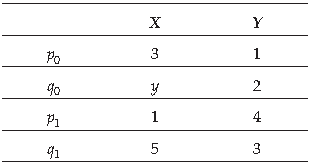
If ratio of Laspeyre’s (L) and Paasche’s (P) index number i.e. L : P = 45 : 34. Then, value of y is
(a) 1
(b) 4
(c) 2
(d) 3
Answer
A
42. For a Poisson distribution, 3P(X = 2) = P(X = 4). Then, P(X = 3) is (given e-6 = 0.00248)
(a) 0.0732
(b) 0.123
(c) 0.0543
(d) 0.0893
Answer
D
43. For a normal distribution, if x % of measurement differ from the mean by less than one fourth of the standard deviation, then the approximate value of x is
(a) 10
(b) 20
(c) 15
(d) 24
Answer
B
44. Three persons, A, B and C invested ₹ 3000, ₹ 5000 and ₹ 7000 respectively, to start a business. At the end of the year, the profit is ₹ 100000, out of which 25% goes for charity. B’s share greater than A’s share by
(a) ₹ 20000
(b) ₹ 10000
(c) ₹ 5000
(d) None of these
Answer
B
45. If the time taken by pipe A to fill the tank is 16 min more than the time taken by pipes A and B together to fill the tank and pipe B takes 25 min more than the time taken by pipes A and B together to fill the tank, then the time taken by both pipes A and B together to fill the tank is
(a) 18 min
(b) 28 min
(c) 20 min
(d) 41 min
Answer
C
Case Study
A wire of length 36 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle.
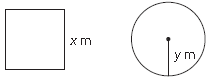
The side of square is xm and radius of the circle is ym.
On the basis of above information, answer the following questions.
46. The relation between x and y, is
(a) 2x + πy = 36
(b) 2x + πy = 18
(c) 2x + πy = 9
(d) None of these
Answer
B
47. The combined area, A of square and circle is given by
(a) A = x2 + πy2
(b) A = x2 + 2πy2
(c) A = 4xx2 + πy2
(d) None of these
Answer
A
48. The value of dA/dx is

Answer
C
49. The value of x when A is minimum, is
(a) 9/π + 4
(b) 18/π + 4
(c) 36/π + 4
(d) 72/π + 4
Answer
C
50. The value of y when A is minimum, is
(a) 9/π + 4
(b) 18/π + 4
(c) 36/π + 4
(d) 72/π + 4
Answer
B

