Please refer to Areas Of Parallelograms And Triangles Class 9 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Mathematics Areas Of Parallelograms And Triangles Notes and Questions
Parallelograms On The Same Base And Between Same Parallel Lines
Let us consider the following figure.
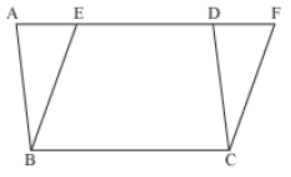
This figure consists of two parallelograms – parallelogram ABCD and parallelogram EBCF.
Can we find the similarities in these two parallelograms?
The property and its converse can be stated as
Parallelograms on the same base and between the same parallels are equal in area.
Parallelograms on the same base and having equal areas lie between the same parallels.
Let us discuss some examples using the above properties.
Example 1: Find the height of a parallelogram if the area of the parallelogram is equal to the area of a rectangle whose length is 6 cm and breadth is 4 cm and both have a common base 6 cm.
Solution:
The figure for the given situation can be drawn as follows.
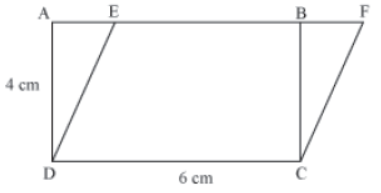
Here, both parallelogram EFCD and rectangle ABCD lie on the same base CD and have equal
area .Thus, they lie between the same parallels.
∴ Height of parallelogram = height of rectangle
Thus, height of parallelogram = 4 cm
Example 2: In the given figure, if the area of parallelogram BCFE is 16 cm2, then find the side of the square ABCD.
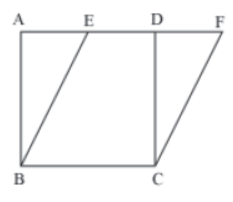
Solution:
Square ABCD and parallelogram BCFE lie on the same base BC and between the same
parallels AF and BC.
We know that the parallelograms on the same base and between the same parallels are
equal in area.
∴ area (ABCD) = area (BCFE)
area (ABCD) = 16 cm2
We know that area of square (ABCD) = side × side
⇒ (side)2 = 16 cm2
Side = 4 cm
Thus, side of the square ABCD is 4 cm.
Example 3: In the given figure, O and D respectively are the mid points of sides AB and EF of a rectangle and ABCD is a parallelogram.
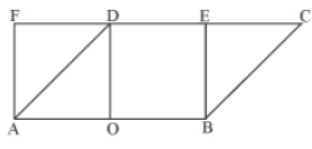
Prove that
area (AOD) + area (BEC) = area (BODE)
Solution:
It is given that O and D are the mid points of sides AB and EF respectively.
∴ AO = OB
Now, parallelograms AODF and BODE lie on equal bases AO and OB and between the same
parallels AB and EF.
∴ area (AODF) = area (BODE) … (i)
Also, parallelograms ABEF and ABCD lie on the equal base AB and between the same
parallels AB and CF.
∴ area (ABEF) = area (ABCD)
On subtracting area (BODE) from both sides, we obtain
area (ABEF) – area (BODE) = area (ABCD) – area (BODE)
area (AODF) = area (AOD) + area (BEC)
Using equation (i), we obtain
area (BODE) = area (AOD) + area (BEC)
Hence, proved.
A Parallelogram and a Triangle Lying on The Same Base and between The Same Parallel Lines
Parallelogram and Triangle on the Same Base and Between the Same Parallel Lines
Imagine a field in the shape of a parallelogram, divided into three parts as is shown in the figure.
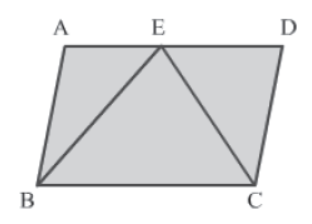
Let us say a farmer wants to sow wheat and pulses in an equal amount in this field. He achieves his objective by sowing wheat in the triangular portion EBC and pulses in the rest of the field. Here we see the farmer applying an important geometric property which can be stated as follows:
If a triangle and a parallelogram are on the same base and between the same parallel lines, then the area of the triangle is half the area of the parallelogram.
Go through this lesson to clarify the above concept. We will also prove this geometric property and solve some examples based on it.
Activity to Prove the Relation
Let us take two parallel lines l and m such that the distance between them is h.
Now, let us take any two points Q and R on the line m such that QR = a.
Taking the base as QR, let us draw few triangles namely ΔPQR, ΔNQR,, ΔOQR, and ΔLQR between the parallel lines l and m.
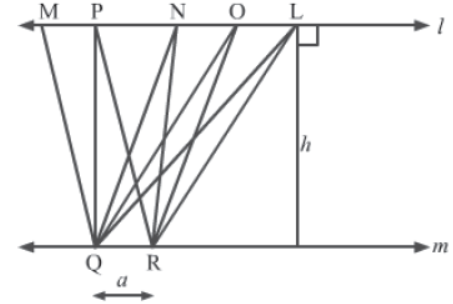
It can be observed from the figure that the base of all these four triangles is QR and height of each triangle is h.
Ar(ΔPQR) = Ar(ΔNQR) = Ar(ΔOQR) = Ar(ΔLQR) = 1/2 x base x height = 1/2 ah
Thus, the triangles lying between the same parallel lines and having the common base are of equal area.
Now, let us consider the parallelogram MPRQ.
Ar(MPRQ) = base × height = ah …(2)
From (1) and (2), we obtain
Ar(ΔPQR) = 1/2 Ar(MPRQ)
Thus, when a triangle and a parallelogram have common base and they lie between the same parallel lines then the area of the triangle is half the area of parallelogram.
Solved Examples Easy
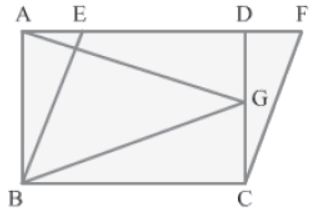
Example 1: AB||DC and BC||AF in the figure. Prove that the area of ΔAGB is equal to half the area of parallelogram BCFE.
Solution:
In the given figure, ΔABG and parallelogram ABCD lie on the same base AB and between the same parallel lines AB and DC.
∴ Area (ABG) = 1/2 Area (ABCD) … (1)
Also, parallelograms ABCD and BCFE lie on the same base BC and between the same
parallel lines BC and AF.
∴ Area (ABCD) = Area (BCFE) … (2)
Hence, from equations 1 and 2, we obtain:
Area (ABG) = 1/2 Area (BCFE)
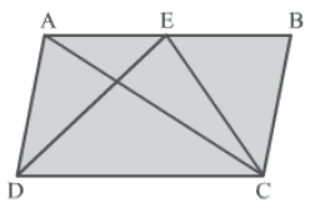
Example 2: In the figure, prove that the area of ΔECD is equal to the area of ΔABC if ABCD is a parallelogram.
Solution:
Parallelogram ABCD and ΔADC lie on the same base DC and between the same parallel lines AB and DC.
∴ Area (ADC) = 1/2 Area (ABCD)… (1)
Also, parallelogram ABCD and ΔECD lie on the same base DC and between the same parallel
lines AB and DC.
∴ Area (ECD) = 1/2 Area (ABCD)… (2)
Using equations 1 and 2, we get:
Area (ADC) = Area (ΔECD) … (3)
We know that a diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area (ADC) = Area (ABC)… (4)
Thus, using equations 3 and 4, we get:
Area (ECD) = Area (ABC)
Medium
Example 1: In the figure, XY||BC, BE||CA and CF||BA. The lines BE and CF meet XY at points E and F respectively. Prove that the area of ΔABE is equal to the area of ΔACF.
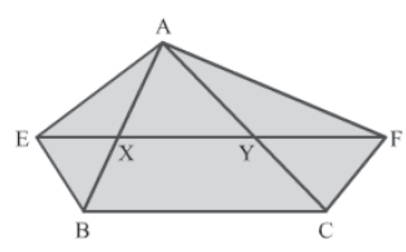
Solution:
In the given figure, ΔABE and parallelogram BCYE lie on the same base EB and between the same parallel lines EB and AC.
∴ Area (ABE) = 1/2 Area (BCYE) … (1)
Similarly,
Area (ACF) = 1/2 Area (CBXF) … (2)
Parallelograms BCYE and CBXF lie on the same base BC and between the same parallel lines
BC and EF.
∴ Area (BCYE) = Area (CBXF) … (3)
Thus, using equations 1, 2 and 3, we get:
Area (ABE) = Area (ACF)
Example 2: In the given figure, G is an interior point of the parallelogram PQRS. Show that:
Area of ΔPGQ + Area of ΔRGS = Area of ΔPGS + Area of ΔRGQ
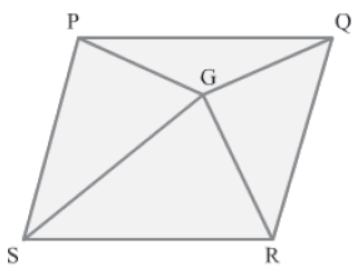
Solution:
It is given that G is an interior point of the parallelogram PQRS.
Construction: Let us draw a line BA parallel to PQ and SR and passing through point G.
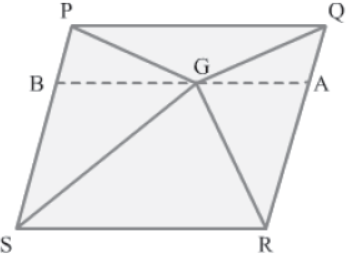
Now, ΔPGQ and parallelogram PQAB are on the same base PQ and between the same parallel lines PQ and BA.
∴ Area (PGQ) = 1/2 Area (PQAB) … (1)
Similarly,
Area (RGS) = 1/2 Area (BARS) … (2)
On adding equations 1 and 2, we obtain:
Area (PGQ) + Area (RGS) = 1/2 Area (PQAB) + 1/2 Area (BARS)
⇒ Area (PGQ) + Area (RGS) = 1/2 [Area (PQAB) + Area (BARS)]
⇒ Area (PGQ) + Area (RGS) = 1/2 Area (PQRS)… (3)
It is clear from the figure that:
Area (PQRS) = Area (PGQ) + Area (RGS) + Area (PGS) + Area (RGQ)
⇒ Area (PQRS) = 1/2 Area (PQRS) + Area (PGS) + Area (RGQ)(Using equation 3)
⇒ Area (PQRS) − 1/2 Area (PQRS) = Area (PGS) + Area (RGQ)
⇒ 1/2 Area (PQRS) = Area (PGS) + Area (RGQ)… (4)
Finally, using equations 3 and 4, we obtain:
Area (PGQ) + Area (RGS) = Area (PGS) + Area (RGQ)
Hard
Example 1: In the figure, PQRS is a parallelogram and M and N are the midpoints of RQ and SR respectively. Prove that:
Area of ΔPMN =3/8 Area of parallelogram PQRS
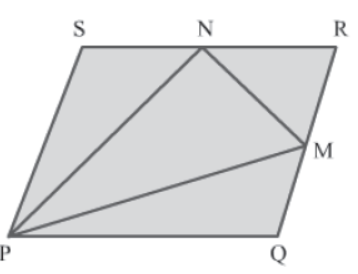
Solution:
Construction: Join Q to S and draw a line XM parallel to PQ and SR.
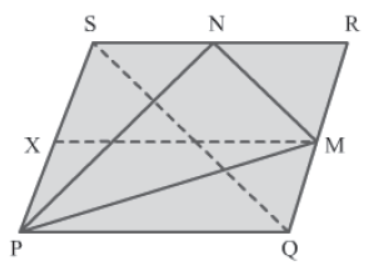
In ΔQRS, M and N are the midpoints of RQ and RS respectively.
∴ MN||QS and MN = 1/2 QS (By midpoint theorem)
Also,
Area (RMN) = 1/4 Area (QRS)
⇒ Area (RMN) = 1/4 x 1/2 Area (PQRS) [&becauseArea (QRS) = 1/2 Area (PQRS)]
⇒ Area (RMN) = 1/8 Area (PQRS) … (1)
Parallelograms XMRS and PQMX lie between the same parallel lines PS and QR and on equal bases (RM = QM).
∴ Area (XMRS) = Area (PQMX) = 1/2 Area (PQRS)
Also,
Area (PQM) = 1/2 Area (PQMX)
⇒ Area (PQM) = 1/2 x 1/2 Area (PQRS)
⇒ Area (PQM) = 1/4 Area (PQRS) … (2)
Similarly,
Area (PNS) = 1/4 Area (PQRS) … (3)
On adding equations 1, 2 and 3, we get:
Ar. (RMN) + Ar. (PQM) + Ar. (PNS) = 1/8 Ar. (PQRS) + 1/4 Ar. (PQRS) + 1/4 Ar. (PQRS)
Area (RMN) + Area (PQM) + Area (PNS) = (1/8+1/4+1/4) Area (PQRS)
Area (RMN) + Area (PQM) + Area (PNS) = 5/8 Area (PQRS)
Hence, we get:
Area (PMN) = Area (PQRS) − 5/8 Area (PQRS)
⇒ Ar (PMN) = 3/8 Area (PQRS)
Example 2: In the figure, ABCD is a parallelogram. If GH||DA and EF||AB, then show that:
Area of ΔAGH + Area of ΔHCB = Area of ΔEDI + Area of ΔAEJ.
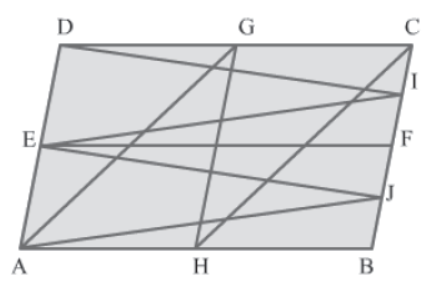
Solution:
It is given that ABCD is a parallelogram.
AB||CD (Opposite sides of a parallelogram)
EF||AB (Given)
Therefore, AEFB and EDCF are parallelograms.
Parallelogram AEFB and ΔAEJ lie on the same base AE and between the same parallel lines EA and FB.
∴ Area (AEJ) = 1/2 Area (AEFB)… (1)
Parallelogram EDCF and ΔEDI lie on same base DE and between the same parallel lines DE and CF.
∴ Area (EDI) = 1/2 Area (EDCF) … (2)
On adding equations 1 and 2, we get:
Area (AEJ) + Area (EDI) = 1/2 Area (AEFB) + 1/2 Area (EDCF)
Area (AEJ) + Area (EDI) = 1/2 Area (AEFB) + 1/2 Area (EDCF)
⇒ Area (AEJ) + Area (EDI) = 1/2 Area (ABCD) … (3)
Now, we know that:
DA||CB (Opposite sides of a parallelogram)
GH||DA (Given)
Therefore, AHGD and HBCG are both parallelograms.
We also know that a diagonal of a parallelogram divides it into two triangles of equal area.
So, in parallelogram AHGD, the diagonal AG divides it into two triangles of equal area, i.e., ΔADG and ΔAGH.
∴ Area (AGH) = 1/2 Area (AHGD) … (4)
Similarly, in parallelogram HBCG, the diagonal HC divides it in two triangles of equal area, i.e., ΔHGC and ΔHCB.
∴ Area (HCB) = 1/2 Area (HBCG) … (5)
On adding equations 4 and 5, we get:
Area (AHG) + Area (HCB) = 1/2 Area (AHGD) + 1/2 Area (HBCG)
⇒ Area (AHG) + Area (HCB) = 1/2 Area (ABCD) … (6)
Finally, using equations 3 and 6, we get:
Area (AEJ) + Area (EDI) = Area (AGH) + Area (HCB)
Triangles on The Same Base and between The Same Parallels
Take a look at the picture of a bridge shown below. Have your ever seen bridges such as this one?

You will notice that this bridge has several irons beams arranged triangularly between horizontal parallel beams on either side. The triangles formed between the parallel beams
are all of the same area. Such an arrangement ensures that the load of traffic does not result in bridge failure. The use of the triangular shape for this purpose is because this shape does not deform easily. This shape is unlike, say, the rectangular shape which can deform easily under force.
In this lesson, we will learn and prove the geometric property that two triangles on the same base (or equal bases) and between the same parallel lines are equal in area. We will also solve some examples based on this property.
Converse of the Property
For the property ‘two triangles lying on the same base (or equal bases) and between the same parallel lines are equal in area,’ the converse is also true. The converse of this property is stated as follows:
If two triangles of equal area lie on the same base, then they should lie between the same parallel lines.
Consider the following figure.
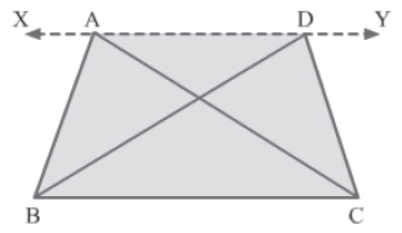
In this figure, ΔABC and ΔDBC lie on the same base BC. According to the above theorem, if the area of ΔABC is equal to the area of ΔDBC, then XY is parallel to BC.
Median of a Triangle Divides It into Two Triangles of Equal Area
Let us consider a ΔPQR with a median PS.
Let us draw a line AB passing through P and parallel to RQ.
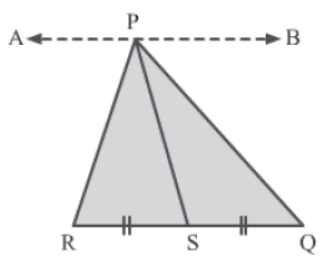
Now, in ΔPQR, PS is a median.
∴ RS = SQ
ΔPSR and ΔPSQ lie on equal bases and between the same parallel lines AB and RQ.
∴ Area (PSR) = Area (PSQ)
So, we can say that a median of a triangle divides the triangle into two triangles of equal area.
Solved Examples
Easy
Example 1: In a ΔABC, P and Q are points on the sides AB and AC respectively. If the area of ΔPBC is equal to the area of ΔQBC, then prove that PQ is parallel to BC.
Solution:
Using the given information, the ΔABC can be drawn as is shown.
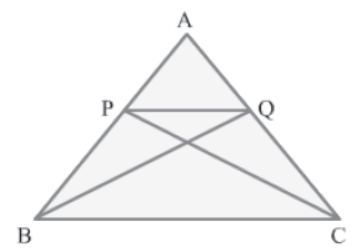
It is given that:
Area (PBC) = Area (QBC)
Now, these triangles lie on the common base BC.
We know that if two triangles of equal area lie on the same base, then they should lie
between the same parallel lines. So, we can say that ΔPBC and ΔQBC lie between the same
parallel lines PQ and BC.
∴ PQ||BC
Example 2: In the shown trapezium ABCD, DC = 2AB. A line segment BG is drawn parallel to AD such that G is the midpoint of DC. Prove that:
Area of ΔABD = Area of ΔBCG
Solution:
Construction:Join B to D to form ΔABD.
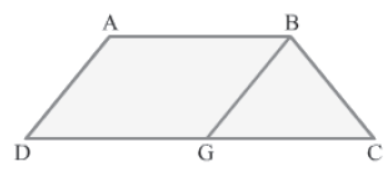
We know that:
AD||BG (Given)
AB||DC (&because ABCD is a trapezium)
We also know that if two pairs of opposite sides of a quadrilateral are parallel, then the
quadrilateral is a parallelogram.
Therefore, ABGD is a parallelogram.
Now, DB is a diagonal of the parallelogram ABGD. A diagonal of a parallelogram divides it
into two congruent triangles.
∴ Area (ABD) = Area (DGB) … (1)
It is given that G is the midpoint of DC.
∴ DG = GC
We know that triangles on equal bases and between the same parallel lines are equal in area.
∴ Area (DGB) = Area (BCG) … (2)
Hence, on using equations 1 and 2, we get:
Area (ABD) = Area (BCG)
Medium
Example 1: In the figure, WX||LM||ZY. Prove that: Area of ΔXLY = Area of ΔWMZ
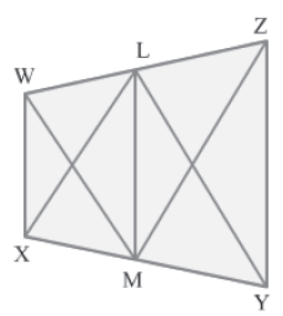
Solution:
It is given that WX||LM.
ΔXLM and ΔWML lie on the same base LM and between the same parallel lines WX and LM.
∴ Area (XLM) = Area (WML) … (1)
It is also given that LM||ZY.
ΔZML and ΔYLM lie on the same base LM and between the same parallel lines LM and ZY.
∴ Area (YLM) = Area (ZML) … (2)
Finally, on adding equations 1 and 2, we obtain:
Area (XLM) + Area (YLM) = Area (WML) + Area (ZML)
⇒ Area (XLY) = Area (WMZ)
Example 2: In the shown ΔPQR, S is the midpoint of QR and T is the midpoint of PS.
Prove that:
Area of ΔPQR = 4 × Area of ΔQTS
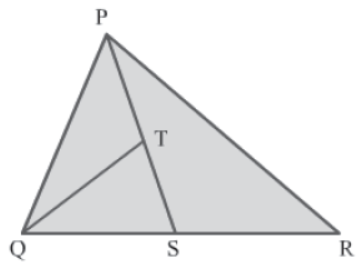
Solution:
It is given that S is the midpoint of QR in ΔPQR. So, PS is a median of the triangle. We know that a median of a triangle divides the triangle into two triangles of equal area.
∴ Area (PQS) = Area (PRS)
⇒ Area (PQS) = 1/2 Area (PQR) … (1)
Similarly, in ΔPQS, QT is a median since T is the midpoint of PS.
∴ Area (QTS) = Area (QPT)
⇒ Area (QTS) = 1/2 Area (PQS) … (2)
Finally, from equations 1 and 2, we get:
Area (QTS) = 1/2 x 1/2 Area (PQR)
⇒ Area (QTS) = 1/4 Area (PQR)
⇒ Area (PQR) = 4 × Area (QTS)
Hard
Example 1: In the figure, QC = CB and ABCD is a parallelogram. Prove that:
Area of ΔBPC = Area of ΔQDP
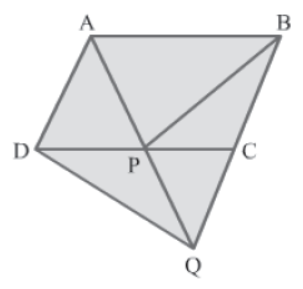
Solution:
Construction:Join A to C to form a diagonal of parallelogram ABCD.
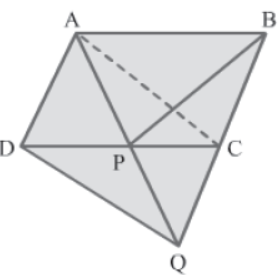
ΔACP and ΔBPC lie on the same base PC and between the same parallel lines PC and AB.
∴ Area (ACP) = Area (BPC) … (1)
AD = BC (&because ABCD is a parallelogram)
QC = CB (Given)
∴ AD = QC
Also, AD||QC
In quadrilateral ACQD, one pair of opposite sides is parallel and equal. Therefore, ACQD is a parallelogram.
Also, AQ and DC are the two diagonals of parallelogram ACQD. We know that the diagonals of a parallelogram bisect each other.
∴ AP = PQ and DP = PC
In ΔACP and ΔQDP:
AP = PQ (Proved above)
∠APC = ∠QPD (Vertically opposite angles)
DP = PC (Proved above)
∴ ΔACP ΔQDP
We know that congruent triangles are equal in area.
∴ Area (ACP) = Area (QDP) … (2)
Hence, from equations 1 and 2, we get:
Area (BPC) = Area (QDP)
Example 2: In the shown trapezium ABCD, F is the midpoint of BC. AB is produced to E, such that DE||CB. If the area of trapezium ABCD is equal to the area of quadrilateral AEDF, then prove that the area of ΔEAD is equal to the area of ΔAFD.
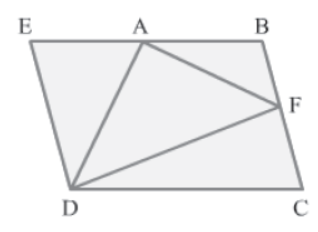
Solution:
Construction: Join A to C and B to D.
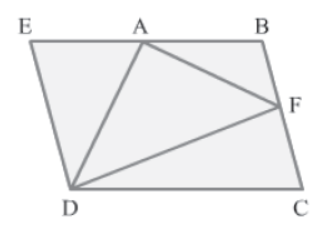
We know that triangles on the same base and between the same parallel lines are equal in area.
ΔBDC and ΔACD lie on the same base DC and between the same parallel lines AB and DC.
∴ Area (BDC) = Area (ACD) … (1)
In ΔBDC, DF is a median. (&because F is the midpoint of BC)
∴ Area (FDC) = 1/2 Area (BDC) … (2)
Similarly, in ΔCAB, AF is a median.
∴ Area (ABF) = 1/2 Area (CAB) … (3)
On adding equations 2 and 3, we get:
Area (FDC) + Area (ABF) = 1/2 [Area (BDC) + Area (CAB)]
⇒ Ar. (ABCD) − Ar. (AFD) = 1/2 [Ar. (ACD) + Ar. (CAB)] (Using equation 1)
⇒ Area (ABCD) − Area (AFD) = 1/2 Area (ABCD)
⇒ 2 × Area (AFD) = Area (ABCD)
It is given that:
Area (ABCD) = Area (AEDF)
∴ 2 × Area (AFD) = Area (AEDF)
⇒ 2 × Area (AFD) = Area (EAD) + Area (AFD)
⇒ Area (AFD) = Area (EAD)
We hope the above Areas Of Parallelograms And Triangles Class 9 Mathematics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 9 Mathematics

