Please refer to Triangles Class 9 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Mathematics Triangles Notes and Questions
SAS Congruence Rule
Congruency of Triangles
Congruency of triangles helps us find solutions to many problems in real life. For example, the distance travelled by a ball in a golf course is easy to measure when the ball is on land; however, when the land is separated by a water body like a pond or any other thing, the task of measurement becomes difficult. In such cases, we use the concept of congruency.
There are certain rules to check the congruency of triangles. One of these is the SAS (Side- Angle-Side) congruence rule. In this lesson, we will learn this rule and its applications.
SAS Congruence Rule
Consider a triangle two of whose sides and the included angle are known. We can check for the congruency of this triangle with respect to another triangle if we know the corresponding sides and angle of that triangle. Two triangles can, thus, be termed ‘congruent’ or ‘incongruent’ by using the SAS congruence rule. This rule states that:
If two sides of a triangle and the angle between them are equal to the corresponding sides and angle of another triangle, then the two triangles are congruent.
Look at the given ΔABC and ΔPQR.

Let us consider sides AB and AC and the included ∠BAC in ΔABC, and the corresponding sides and angle in ΔPQR, i.e., PQ, PR and ∠QPR.
By the SAS congruence rule, the two triangles will be congruent if AB = PQ, AC = PR and ∠BAC = ∠QPR.
Similarly, we can check for congruency by taking other pairs of sides and included angles in these triangles.
Verification of SAS Congruence Rule
The SAS congruence rule for triangles is taken as a postulate, so there is no proof for the same but we we can verify it by doing an activity.
The steps of the activity are as follows:
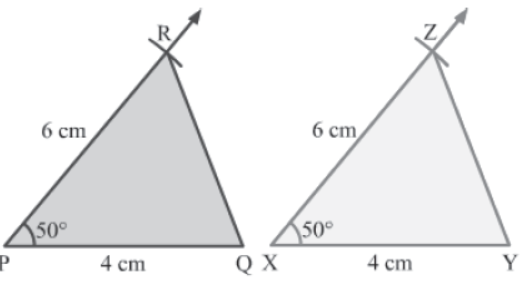
i) Construct ΔPQR such that PQ = 4 cm, PR = 6 cm and ∠QPR = 50°.
ii) Construct ΔXYZ with the same measures such that XY = 4 cm, XZ = 6 cm and ∠YXZ = 50°.
iii) Cut both the triangles along their boundaries.
iv) Try to superpose one triangle by the other. One triangle can be placed on the other in six different ways such that vertex lie on vertex.
v) In one of the the trials, you will get P falling over X, Q falling over Y and R falling over Z.
In this case, you will see that both the triangles cover each other exactly.
vi) Thus, under the correspondence PQR↔XYZ, the triangles are congruent.
This verifies the SAS congruence rule.
CPCT
CPCT stands for ‘corresponding parts of congruent triangles’. ‘Corresponding parts’ means corresponding sides and angles of triangles. According to CPCT, if two or more triangles are congruent to one another, then all of their corresponding parts are equal.
For example, in the given ΔABC and ΔDEF, AB = DE, ∠B = ∠E and BC = EF. So, according to the SAS congruence criterion, we have ΔABC ≅ΔDEF.

Now, by CPCT, we can say that the remaining corresponding parts of the two congruent
triangles are also equal. This means that AC = DF, ∠A = ∠D and ∠C = ∠F.
Similarly, we can apply CPCT in case of other congruent triangles.
In a right angled triangle, median drawn to the hypotenuse from the opposite vertex is equal to the half of the hypotenuse.
Let us prove the theorem.
Given: Right angled ΔPQR, ∠PQR = 90° and median QS to hypotenuse PR.
To prove: QS = 1/2 PR
Construction: Extend QS to T such that QS = ST and join T to R.

Proof:
In ΔPSQ and ΔRST, we have
QS = TS (By construction)
∠PSQ = ∠RST (Vertically opposite angles)
PS = RS (Given)
So, by SAS congruence criterion, we have
ΔPSQ ≅ ΔRST
∴ PQ = RT …(1) (By CPCT)
And ∠QPS = ∠TRS (By CPCT)
Thus, PQ || RT (∠QPS and ∠TRS alternate interior angles formed by transversal PR)
Now, QR is also a transversal to parallel line segments PQ and RT.
∠PQR + ∠TRQ = 180° (Sum of interior angles on the same side of transversal)
But ∠PQR = 90°
∴ ∠TRQ = 90° (2)
In ΔPQR and ΔTRQ, we have
PQ = RT [From (1)]
∠PQR = ∠TRQ = 90°
QR = QR (Common side)
So, by SAS congruence criterion, we have
ΔPQR ≅ ΔTRQ
∴ PR = QT (By CPCT)
⇒ 1/2 PR = 1/2 QT
But 1/2 QT = QS
∴ QS = 1/2 PR
Hence, proved.
ASA Congruence Rule
ASA Congruence Rule
Look at the given figure.

Observe how the ladder, the wall and the horizontal together make triangles in the figure. It can be seen that the angle marked between the ladder and the wall on the left is greater than the same angle marked on the right. Clearly, the triangles are not congruent although it is the same ladder on both sides.
Both angles and sides play an important role in determining the congruency of triangles. In this lesson, we will discuss the ASA (Angle-Side-Angle) congruence rule and solve some problems based on it.
ASA Congruence Rule
The ASA congruence rule for triangles states that:
If two angles of a triangle and the side between them are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
Consider the given ΔABC and ΔPQR.

Observe how corresponding components of the two triangles are marked.
Now, by the ASA congruence rule, the two triangles will be congruent if these
corresponding components are equal, i.e., if ∠ABC = ∠PQR, BC = QR and ∠ACB = ∠PRQ, then ΔABC ≅ ΔPQR.
Note that, under the above condition of congruence, we cannot write ΔABC ≅ ΔQRP. The order of the vertices matters in any congruency.
Did You Know?
A bright meteor was seen in the sky above Greenland on December 9, 1997. In an attempt to find the fragments of the meteorite, scientists collected data from eyewitnesses who observed the meteor passing through the sky. As is shown in the figure below, the scientists considered sightlines of observers in different towns.
One such sightline was of observers in the town called Paamiut (Point P). Another was of observers in the town called Narsarsuaq (Point N). Using the ASA congruence rule, the scientists were able to gather enough information to successfully locate the fragments of the meteorite (Point M).
Proof of the ASA Congruence Rule: Case 1
Let us consider ΔABC and ΔDEF such that ∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF. By the
ASA congruence rule, ΔABC and ΔDEF are congruent. By CPCT, we have AB = DE.
Case 1: Let us prove ΔABC ≅ ΔDEF by taking AB = DE.

In this case, we have
AB = DE (Given)
∠ABC = ∠DEF (Given)
BC = EF (Given)
So, by the SAS congruence rule, we have:
ΔABC ≅ ΔDEF
Proof of the ASA Congruence Rule: Case 2
Let us consider ΔABC and ΔDEF such that ∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF. By the
ASA congruence rule, ΔABC and ΔDEF are congruent. By CPCT, we have AB = DE. Let us
assume AB ≠ DE.
Case 2: Let us prove ΔABC ≅ ΔDEF by taking AB < DE.
Construction: Mark a point G on DE such that GE = AB. Join G to F.
Now, in ΔABC and ΔGEF, we have:

AB = GE (By construction)
∠ABC = ∠GEF (∵∠ABC = ∠DEF and ∠DEF = ∠GEF) IMG
BC = EF (Given)
So, by the SAS congruence rule, we obtain:
ΔABC ≅ ΔGEF
⇒ ∠ACB = ∠GFE (By CPCT)
But ∠ACB = ∠DFE (Given)
∴ ∠GFE = ∠DFE
This can be possible only when line segment GF coincides with line segment DF or point G coincides with point D. Therefore, AB must be equal to DE and ΔGEF must be ΔDEF.
∴ ΔABC ≅ ΔDEF
Proof of the ASA Congruence Rule: Case 3
Let us consider ΔABC and ΔDEF such that ∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF. By the ASA congruence rule, ΔABC and ΔDEF are congruent. By CPCT, we have AB = DE. Let us
assume AB ≠ DE.
Case 3: Let us prove ΔABC ≅ ΔDEF by taking AB > DE.
Construction: Extend ED to point G such that GE = AB. Join G to F.

Now, in ΔABC and ΔGEF, we have:
AB = GE (By construction)
∠ABC = ∠DEF (∵∠ABC = ∠DEF and ∠DEF = ∠GEF)
BC = EF (Given)
So, by the SAS congruence rule, we obtain:
ΔABC ≅ ΔGEF
⇒ ∠ACB = ∠GFE (By CPCT)
But ∠ACB = ∠DFE (Given)
∴ ∠GFE = ∠DFE
This can be possible only when line segment GF coincides with line segment DF or point G
coincides with point D. Therefore, AB must be equal to DE and ΔGEF must be ΔDEF.
∴ ΔABC ≅ ΔDEF
AAS Congruence Rule
Consider the following triangular clocks.
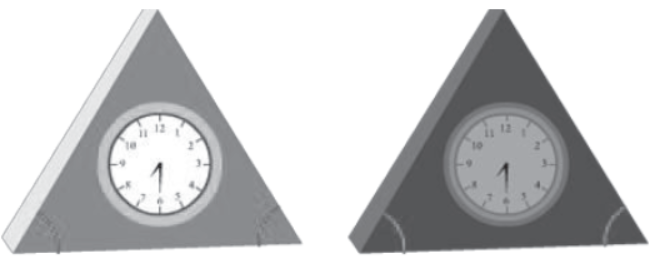
In each clock, two angles on the base are marked. We can check the congruency of the clocks if we know the marked angles and the included side (i.e., the base) by using the ASA congruence rule.
Now, can we check the congruency of these clocks if instead of the base we are given any of the other two sides? Yes, we can do so and this is why we have the AAS (Angle-Angle-Side)
congruence rule. In this lesson, we will discuss this rule and solve some examples related to it.
AAS Congruence Rule
The AAS congruence rule for triangles states that:
If any two angles and one side of a triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
This is nothing but the generalized form of the ASA congruence rule.
Consider the given ΔPQR and ΔXYZ.

In each triangle, the given side is not between the given angles. So, we cannot apply the ASA
congruence rule here. Instead, we will use the AAS congruence rule.
In ΔPQR and ΔYZX, we have:
PQ = YZ = 2 cm
∠PQR = ∠YZX = 40°
∠PRQ = ∠YXZ = 50°
Thus, by using the AAS congruence criterion, we obtain: ΔPQR ≅ ΔYZX
Difference between AAS and ASA
The AAS and ASA criterions are both used for checking or proving congruency of triangles, but there is a subtle difference between the two.
♦ The ASA rule is applied when two interior angles of a triangle and the side between them are considered.
♦ The AAS rule is applied when two interior angles of a triangle and any side other than the one between them are considered.
Take, for example, the given ΔABC and ΔPQR.

To prove ΔABC ≅ ΔPQR by the ASA rule, we need:
∠BAC = ∠QPR, ∠ABC = ∠PQR and AB = PQ
To prove ΔABC ≅ ΔPQR by the AAS rule, we need:
∠BAC = ∠QPR, ∠ABC = ∠PQR and BC = QR
SSS Congruence Rule
Relation between the Congruency of Triangles and Their Sides
Consider the kite shown below.

It can be seen that the red and yellow coloured triangles have equal sides. On the basis of
this information, can we say that the two triangles are congruent? Or, to rephrase the question, do the sides of triangles determine the congruency of the triangles? Yes, they do, and this is why we have the SSS (Side-Side-Side) congruence rule.
In this lesson, we will discuss the SSS congruence rule and its proof. We will also crack some problems based on it.
SSS Congruence Rule
Statement: Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.
Given: ΔABC and ΔDEF such that AB = DE, BC = EF and AC = DF
To prove: ΔABC ≅ ΔDEF
Construction: Suppose BC and EF are the longest sides of the two triangles. Draw EG such that ∠GEF = ∠ABC and GE = AB. Join point G to points F and D.

Proof: In ΔABC and ΔGEF, we have:
BC = EF (Given)
AB = GE (By construction)
∠ABC = ∠GEF (By construction)
So, by the SAS congruence rule, we have:
ΔABC ≅ ΔGEF
⇒ ∠BAC = ∠EGF and AC = GF (By CPCT)
Now, AB = DE and AB = GE
⇒ DE = GE … (1)
Similarly, AC = DF and AC = GF
⇒ DF = GF … (2)
In ΔDEG, we have:
DE = GE (From equation 1)
⇒ ∠EDG = ∠EGD … (3)
In ΔDFG, we have:
DF = GF (From equation 2)
⇒ ∠FDG = ∠FGD… (4)
On adding equations 3 and 4, we get:
∠EDG + ∠FDG = ∠EGD + ∠FGD
⇒ ∠EDF = ∠EGF
We know that ∠EGF = ∠BAC (Proved above)
∴ ∠BAC = ∠EDF … (5)
Thus, in ΔABC and ΔDEF, we have:
AB = DE (Given)
∠BAC = ∠EDF (From equation 5)
AC = DF (Given)
So, by the SAS congruence rule, we obtain:
ΔABC ≅ ΔDEF
Hence, the SSS congruence rule holds true.
RHS Congruence Rule
RHS Congruence Rule
Right angles are all around us. For example, while building houses, the walls are kept at a right angle to the horizontal. Different square and rectangular figures surround us and all of them consist of right angles. The following figure also shows right angles.

In the figure, the pieces of bread resemble right-angled triangles. They also seem to be congruent. Right-angled triangles are special and their congruency is checked by a special congruence rule known as the RHS (Right-Hypotenuse-Side) rule.
We will study the RHS congruence rule in this lesson and solve some examples to familiarize ourselves with the concept.
RHS congruence theorem: Two right-angled triangles are congruent if the hypotenuse and a side of one triangle are equal to the hypotenuse and the corresponding side of the other triangle.

Given: Two right-angled triangle ABC and DEF such that ∠B = ∠E = 90°; Hypotenuse AC =
Hypotenuse DF and AB = DE.
To prove: ΔABC ≅ ΔDEF.
Construction: Produce FE to G so that EG = BC and join DG.
Proof:
In triangles ABC and DEF,
AB = DE (Given)
BC = EG (By construction)
∠ABC= ∠DEF (Each equal to 90°)
Thus, by SAS congruence criterion,
ΔABC ≅ ΔDEG
⇒ ∠ACB = ∠ DGE and AC = DG (CPCT)
Given, AC = DF
∴ DG = AC = DF
In ΔDGF, we have
DG = DF
∠G = ∠F (Angles opposite to equal sides are equal)
In ΔDEF and ΔDEG,
∠G = ∠F (Proved)
∠DEG = ∠DEF (Both equal to 90°)
Thus, ∠GDE = 180° – (∠G + ∠DEG) = 180° – (∠F +∠DEF) = ∠FDE
In ΔDEG and ΔDEF,
DG = DF (Proved)
DE = DE (Common)
∠GDE = ∠FDE (Proved)
Thus, by SAS congruence criterion
ΔDEG ≅ ΔDEF
But, we have ΔABC ΔDEG
Thus, ΔABC ΔDEF
Whiz Kid
RHS congruence rule was used by the famous ancient Greek mathematician Thales to calculate the distance of a ship anchored at sea from the shore. For this, he stuck three poles on the shore such that the first one was directly in front of the ship, the second was at some distance from the first pole and the third was exactly between the other two poles. He then walked backward along a line from the second pole perpendicular to the shore until the middle pole and the ship were in the same line of sight. Then, he marked his position.
This is shown in the following figure.

It can be seen that the triangle formed on the sea is congruent to the triangle formed on the shore by the RHS rule. So, the distance between the ship and the shore is equal to the distance between the second pole and the spot where Thales stands.
Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
Isosceles Triangles around Us
You must have seen triangular clothes hangers or coat hangers such as the one shown.

What do you observe about the sides of the hanger? The base is clearly the longest side, while the other two sides are equal. We know that a triangle with any two sides equal is called an isosceles triangle. So, the hanger is a real-life example of an isosceles triangle.
Another example of an isosceles triangle is the roof of a hut. Yet another example is a diagonally cut slice of bread.
You can see that the angles opposite the equal sides of the clothes hanger are equal. In this lesson, we will discuss about the same, i.e., angles opposite equal sides of an isosceles triangle. We will also solve some problems based on this concept.
Know Your Scientist

Did You Know?
The word ‘isosceles’ is a combination of the Greek words ‘isos’meaning‘equal’ and ‘skelos’ meaning‘leg’. So, a triangle having two equal legs is called an isosceles triangle.
Know More
♦ The altitude to the base of an isosceles triangle bisects the vertex angle.
♦ The altitude to the base of an isosceles triangle bisects the base.
♦ When the equal sides are at right angle, the triangle is called a ‘right isosceles triangle’.
Whiz Kid
In an isosceles triangle, the orthocentre, the centroid, the incentre and the circumcentre, all lie on the median to the base.
Orthocentre: It is the point where the altitudes of the three sides of a triangle intersect.

In ΔABC, O is the orthocentre.
Centroid: It is the point where the medians of the three sides of a triangle intersect.

In ΔABC, G is the centroid.
Incentre: It is the point where the interior angle bisectors of a triangle intersect.
In ΔABC, I is the incentre.
Circumcentre: It is the point where the perpendicular bisectors of the three sides of a triangle intersect.
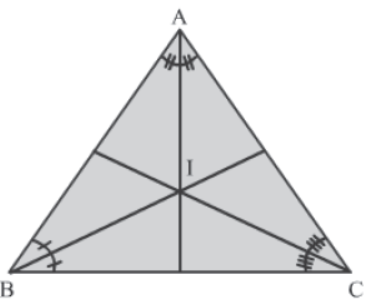
In ΔABC, D is the circumcentre.
Sides Opposite to Equal Angles of a Triangle are Equal
Observing the Equal Angles and the Sides Opposite to Them in an Isosceles Triangle
Consider the following ΔPQR.
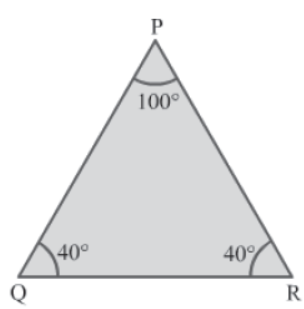
Is ΔPQR isosceles? We know that if two sides of a triangle are equal (or congruent), then the triangle is isosceles. However, in ΔPQR, two angles are equal (or congruent). We have studied that the angles opposite to equal (or congruent) sides of an isosceles triangle are equal (or congruent). Is the converse of this property also true?
In this lesson, we will study about the equality of sides opposite equal angles in an isosceles triangle. We will also solve some examples related to this concept.
Whiz Kid
In an isosceles triangle, the medians drawn from the base vertices to the opposite sides are of equal length.
For example:

The shown ΔABC is isosceles such that AB = AC. BD and CE are the respective medians from vertices B and C to sides AC and AB. Therefore, BD = CE.
Observing the Relation between the Angles and Sides of a Triangle IMG
Harsh is flying a kite. The thread of the kite makes angle x with the vertical, as is shown in the figure. Sometime later, he gives the thread to his friend Mohit who is standing some
distance away from him. At that position, the thread makes angle y with the vertical.
The figure clearly shows that angle y of ΔACD is greater than angle x of ΔABD. Also, side AC is greater than side AB. This shows us that if we increase the length of any side of a triangle, then the angle facing that side also increases.
In this lesson, we will discuss the relation between the angles and sides of a triangle. We will then solve some examples relating to the same.
Triangle Inequality Theorem
We know that if two sides of a triangle are equal, then the angles opposite these sides are also equal. Now, what if all the sides of a triangle are unequal? What can be said about
its angles?The triangle inequality theorem describes such a triangle. It states that:
If two sides of a triangle are unequal, then the longer side has the greater angle opposite it.
Consider the given ΔABC.
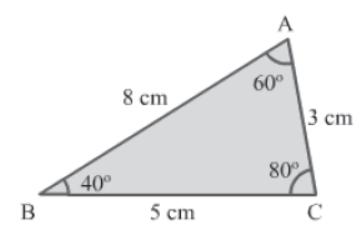
Let us apply the stated theorem in this triangle.
AB = 8 cm is the longest side in ΔABC. Therefore, the angle opposite AB, i.e., ∠BCA is the
greatest angle of the triangle. Also, AC = 3 cm is the shortest side in ΔABC. Therefore, the
angle opposite AC, i.e., ∠ABC is the smallest angle of the triangle.
Thus, we can conclude that the angle opposite the longer side is greater. Therefore, the theorem holds true.
Proving the Triangle Inequality Theorem
Given: ΔPQR in which PR > PQ
To prove: ∠Q > ∠R IMG
Construction: Mark a point S on PR such that PQ = PS. Join Q to S. PP
Proof: In ΔPQS, we have:
PQ = PS (By construction)
⇒ ∠1 = ∠2 … (1) [∵ Angles opposite equal sides are equal]
In ΔQRS, ∠2 is the exterior angle; so, it is greater than the interior opposite angles of ΔQRS.
∴ ∠2 > ∠SRQ
⇒ ∠2 > ∠PRQ … (2) [∵ ∠PRQ = ∠SRQ]
From (1) and (2), we have:
∠1 > ∠PRQ … (3)
Now, ∠1 is a part of ∠PQR.
So, ∠PQR > ∠1 … (4)
Thus, from (3) and (4), we can conclude that:
∠PQR > ∠PRQ
Observation of the Sides of a Triangle by Seeing the Angles
The red car has to travel at an angle of 65°, while the blue car has to travel at an angle of 50° with respect to line AB to reach the finish point C. Do you think any one car has an advantage over the other?
On observing the triangular track, it seems that path BC is longer than path AC. So, clearly, the red car has an advantage over the blue car. Also, the angle opposite BC is greater than the angle opposite AC. So, what does this tell us about the relation between the sides and angles of the triangular racetrack?
Let us go through this lesson to learn about the relation between the sides and angles of a triangle. We will also solve some problems based on this relation.
In a Triangle, the Side Opposite the Greater Angle is
Longer
We have studied that in a triangle having two unequal sides, the angle opposite the longer side is greater. The converse of this property is also true. It states that:
If two angles of a triangle are unequal, then the greater angle has the longer side opposite it. In other words, the smaller angle has theshorter side opposite it.
Consider the following ΔPQR.
Let us apply the stated property in this triangle

∠QPR = 110° is the greatest angle in ΔPQR.
Therefore, the side opposite ∠QPR, i.e., QR is the longest side of the triangle. Also, ∠PQR = 25° is the smallest angle in ΔPQR.
Therefore, the side opposite ∠PQR, i.e., PR is the shortest side of the triangle.
We can apply this property to other triangles as well. Using this property, we can say that in a right triangle, the hypotenuse is the longest side.
Whiz Kid
In trigonometry, a skinny triangle is one whose height is much greater than its base.
The given triangle is an example of a skinny triangle.
Proving the Property
Given: ΔPQR in which ∠Q > ∠R
To prove: PR > PQ.
Proof: In ΔPQR, we can have three possible cases: (1) PQ > PR, (2) PQ = PR and (3) PQ < PR.

CASE 1:
When PQ > PR, we have:
∠R > ∠Q (∵ Angle opposite longer side is greater)
But this contradicts the given hypothesis that ∠R < ∠Q. Thus, PQ > PR is not true.
CASE 2:
When PQ = PR, we have:
∠R = ∠Q (∵ Angles opposite equal sides are equal)
But this too contradicts the given hypothesis that ∠R < ∠Q. Thus, PQ = PR is also not true.
So, we are left with the third possibility, i.e., PQ < PR (or PR > PQ), which must be true.
Thus, we have proven that if two angles of a triangle are unequal, then the greater angle has the longer side opposite it.