Please refer to Circles Class 10 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 10. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 10 Mathematics Circles Notes and Questions
Circles
Concept Of Tangent At Any Point Of The Circle
A circle has important elements such as chords, secants, and tangents.
A tangent at any point of a circle is perpendicular to the radius through the point of contact.
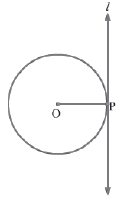
In the above figure O is the centre of circle, line l is the tangent and P is point of contact.
∴ l ⊥ OP
Proof:
It is given that O is the centre of the circle, l is the tangent to this circle and P is the point of contact.

Let us assume l is not perpendicular to the radius of the circle.
In this case, let us draw perpendicular OA to tangent l. Thus, point A is distinct from point P.
Let B be any point on tangent such that BAP is a line and BA = AP.
Now, in ΔOAB and ΔOAP, we have
OA = OA (Common side)
∠OAB = ∠OAP (OA ⊥ tangent l)
BA = AP (By construction)
∴ ΔOAB ΔOAP
∴ OB = OP (By CPCT)
Since OB = OP, point B also lies on the circle.
Also, point B is different from point P.
Thus, tangent l touches the circle at two distinct points. This contradicts the definition of tangent.
Hence, our assumption is wrong.
Therefore, tangent l ⊥OP.
Hence proved.
The converse of this theorem is also true which states that:
The line perpendicular to the radius of a circle at its outer end is tangent to the circle.
Proof:
Let O be the centre of the circle, OP be the radius and l be the line perpendicular to OP such as it passes through point P on the circle.
Also, let A be any point on line l distinct from P.

From the figure, it can be observed that ΔOAP is a right angled triangle.
∴ OA is hypotenuse for ΔOAP.
∴ OA > OP (Radius)
∴ OA is not radius.
∴ Point A does not lie on the circle.
∴ No point of line l other than P lies on the circle.
∴ P is the only point common to the circle and line l.
∴ Line l is tangent to the circle at point P.
Hence proved.
Let us now solve some examples related to the tangents of the circle.
Example 1: Draw a circle with centre O, and two lines such that one is a tangent and other is a secant.
Solution:
The figure can be drawn as follows.
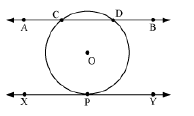

Example 2: Which of the following statements are correct?
(i) There can be only one tangent at a point on the circle.
(ii) Diameter is also a secant of the circle.
Solution:
(i) Correct
(ii) Incorrect
Example 3: A line XY is a tangent of the circle with centre O and radius 6 cm. The point of contact is P, and Q is any point on the tangent XY. If OQ = 10 cm, then what is the length of PQ?
Solution:
The figure can be drawn as follows.
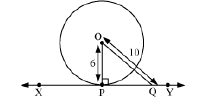
We know that the radius through the point of contact is perpendicular to the tangent.
∴ OP⊥XY
Using Pythagoras theorem in right-angled triangle OPQ, we obtain
(OQ)2 = (OP)2 + (PQ)2
(PQ)2 = (OQ)2 – (OP)2
(PQ)2 = (10)2 – (6)2
(PQ)2 = 100 – 36
(PQ)2 = 64
PQ = 8 cm
Thus, the length of PQ is 8 cm.
Example 4: Two tangents XY and PQ are drawn at the ends of a diameter AB of the circle with centre O. Show that XY ∥ PQ.
Solution:
The figure can be drawn as follows.

XY is a tangent at A and OA is the radius.
We know that the radius through the point of contact is perpendicular to the tangent.
∴ XY⊥OA
⇒ XY⊥AB … (1)
Similarly, PQ⊥AB … (2)
Now, the lines perpendicular to the same line are parallel.
∴ From equations (1) and (2), we obtain
XY || PQ
Hence, proved
Example 5: A circle is inscribed in a triangle such as it touches all the three sides of the triangle. Prove that the area of the triangle is half the product of its perimeter and the radius of circle.
Solution:
Let O be the centre of the circle inscribed in ΔABC.
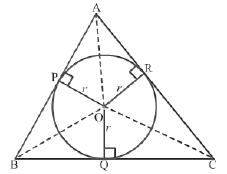
It can be seen that AB, BC and CA are tangents which touches the circle at P, Q and R respectively.
Also, OP, OQ and OR are the radii of the circle.
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, AB ⊥ OP, BC ⊥ OQ and CA ⊥ OR.
Let s be the perimeter of ΔABC.
∴ s = AB + BC + CA
Now,

Hence proved.
Example 6: Observe the given figure.

Find the angle between radii.
Solution:
In the given figure, O is the centre of the circle and OP and OR are the radii. Also, QP and SR are the tangents to the circle at points P and R respectively which intersect each other at
point A.
It is given that,
∠PAS = 110°
We need to find the angle between radii OP and OR i.e., ∠POR.
From the figure, we have
∠PAS + ∠PAR = 180°
⇒ 110° + ∠PAR = 180°
⇒ ∠PAR = 180° – 110°
⇒ ∠PAR = 70°
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, QP ⊥ OP and SR ⊥ OR.
∴ ∠APO = 90° and ∠ARO = 90°
Now, in quadrilateral APOR, we have
∠POR +∠APO + ∠ARO + ∠PAR = 360° (By angle sum property of quadrilaterals)
⇒ ∠POR + 90° + 90° + 70° = 360°
⇒ ∠POR + 250° = 360°
⇒ ∠POR = 110°
Thus, the angle between the radii is 110°.
Tangents Drawn From An External Point To A Circle
We are very well aware of what a tangent is. Now let us look at the following video and find out how many tangents can be drawn to a circle from an external point and if there is any
relation between the lengths of these tangents.
The lengths of the two tangent segments to a circle drawn from an external point are equal.
Proof:
Let P be the point outside the circle having centre O from which the tangents PQ and PR are drawn touching the circle at Q and R respectively.
We have to prove that PQ = PR.
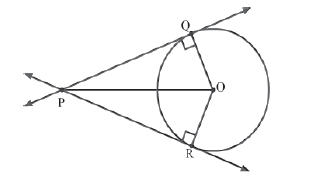
From the figure, it can be observed that OQ and OR are the radii of the circle.
Therefore, ∠PQO = ∠PRO = 90°
Now, in ΔPOQ and ΔPOR, we have
∠PQO = ∠PRO = 90°
PO = PO (Common hypotenuse)
OQ = OR (Radii of same circle)
Using RHS (Right-Hypotenuse-Side) congruence rule, we get
ΔPOQ ≅ ΔPOR
∴ PQ = PR (By CPCT)
Thus, the lengths of the two tangent segments to a circle drawn from an external point are
equal.
Note: Since ΔPOQ ΔPOR, we have
∠OPQ = ∠OPR (By CPCT)
∠POQ = ∠POR (By CPCT)
Thus, the above theorem can be extended as,
(1) The tangents drawn to a circle from an external point are equally inclined to the line joining the external point and the centre.
(2) The tangents drawn to a circle from an external point subtend equal angles at the centre.
Now, let us solve some examples to understand the concept.
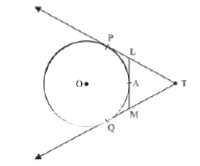
Example 1: In the given figure, prove that TL + AL = TM + AM
Example 2: A circle is circumscribed by a quadrilateral PQRS such that the circle touches all the sides of quadrilateral PQRS at points A, B, C, and D respectively. Show
that
PQ + RS = QR + PS
Solution:
The figure can be drawn as follows.

Now, applying the theorem “The tangents drawn from an external point to the circle are equal in length”, we obtain
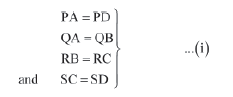
Therefore,
PQ + RS = (PA + QA) + (RC + SC)
= (PD + QB) + (RB + SD) [Using (i)]
= (PD + SD) + (QB + RB)
= PS + QR
Thus, PQ + RS = PS + QR
Hence, proved
Example 3: A circle is inscribed in a triangle ABC such that the circle touches the sides AB, BC, and AC of the triangle at P, Q, and R respectively. What are the lengths of AP, BQ, and CR if AB = 10 cm, BC = 6 cm, and AC = 12 cm.
Solution:
The figure can be drawn as follows.
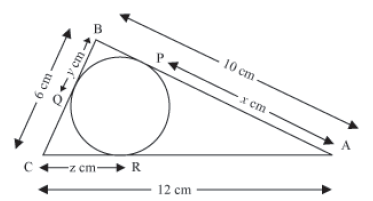
Let AP = x cm, BQ = y cm, and CR = z cm.
Now, applying the theorem “The tangents drawn from an external point to the circle are
equal in length”, we obtain
AP = AR = x
BQ = BP = y
CR = CQ = z
Therefore, we can write
AP + BP = AB
x + y = 10 cm … (i)
BQ + QC = BC
y + z = 6 cm … (ii)
CR + AR = AC
z + x = 12 cm … (iii)
On adding (i), (ii), and (iii), we obtain
2x + 2y + 2z = 28 cm
x + y + z = 14 cm … (iv)
Subtracting (i) from (iv), we obtain
(x + y + z) – (x + y) = 14 – 10
z = 4 cm
Similarly, subtracting (ii) and (iii) respectively from (iv), we obtain
(x + y + z) – (y + z) = 14 – 6
x = 8 cm
(x + y + z) – (z + x) = 14 – 12
y = 2 cm
Thus, AP = 8 cm, BQ = 2 cm, and CR = 4 cm
Example 4: In the given figure, PQR is an isosceles triangle with PQ = PR. A circle, which is inscribed in ΔPQR, touches the sides of the triangle at A, B, and C. Show that AQ = AR.

Solution:
It is given that PQR is an isosceles triangle where
PQ = PR … (i)
Now, the tangents drawn from an external point to a circle are equal in length.
∴ PC = PB … (ii)
On subtracting equation (ii) from equation (i), we obtain
PQ – PC = PR – PB
QC = RB … (iii)
Now, QA and QC are tangents to the circle from point Q.
∴ QA = QC
Similarly, RB = RA
Using the above relations in equation (iii), we obtain
QA = RA
∴ AQ = AR
Example 5: PA and QA are tangents drawn to a circle with centre O. Show that ∠BOQ = ∠PAQ.
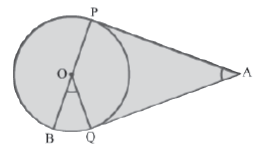
Solution:
Join O with A, P with Q.

We know that, the tangents drawn to a circle from an external point are equal and they are equally inclined to the line joining the external point and the centre.
Therefore, ∠PAO = ∠QAO and ∠POA = ∠QOA.
It is clear that PQ ⊥ OA.
Now, ∠BOQ = 2∠OPQ … (1)
[Angle subtended by an arc at the centre is twice the angle subtended by the same arc at anywhere on the Circle]


We hope the above Circles Class 10 Mathematics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 10 Mathematics


