Please refer to Class 12 Mathematics Sample Paper With Solutions Set G provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
SECTION – A
1. Write a 3 x 3 skew symmetric matrix.
Solution: Example of a 3 x 3 skew symmetric matrix
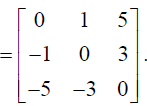
2. Find the product of the order and degree of the following differential equation : x(d2y/dx2)2 + (dy/dx)2 + y2 = 0 .
Solution: Here order and degree of the given differential equation are 2 and 2 respectively. Therefore, the required product is 2 x 2 = 4 .
3. Write a differential equation for y = Acosαx + Bsinβx , where A and B are arbitrary constants.
Solution: Given y = Acosαx + Bsinβx ⇒ dy/dx = -αAsin x + Bα cos αx
⇒ d2y/dx2 = -αA cos αx – Bα2 sin αx = α2 [A cosαx + Bsinαx] = -α2y
∴ d2y/dx2 + α2y = 0 .
4. Write the projection of 2î + 3ĵ – k̂along the vector î + ĵ .
Solution: Projection of 2î + 3ĵ – k̂ along the vector î + ĵ is (2î + 3ĵ – k̂).(î + ĵ)/|î + ĵ| = 2+3 – 0/√12+12 = 5/√2 .We have used, projection of a̅ on b̅ = a̅.b̅ .
5. Write the value of î.(ĵ x k̂) + ĵ.(k̂x î) + k̂.(î x ĵ) .
Solution: We have î.(ĵ x k̂) + ĵ.(k̂x î) + k̂.(î x ĵ) =
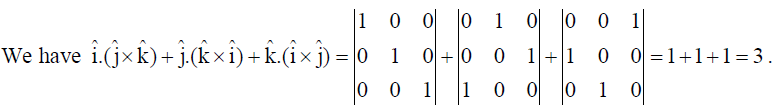
6. Write the direction cosines of the normal to the plane 3x + 4y + 12z = 52.
Solution: The direction ratios of the normal to the plane 3x + 4y +12z = 52 are 3, 4, 12.
So d. c.’s are ± 3/√32 + 42 + 122 , ± 4/√169 , ± 13/13 i.e., ± 3/13 , ± 4/13 , ± 12/13 .
SECTION – B
7. There are 3 families A, B and C. The number of men, women and children in these families are as under :

Daily expenses of men, women and children are ₹ 200, ₹ 150 and ₹ 200 respectively. Only men and women earn and children do not. Using matrix multiplication, calculate the daily expenses of each family. What impact does more children in the family create on the society?
Solution: The given information can be expressed as :
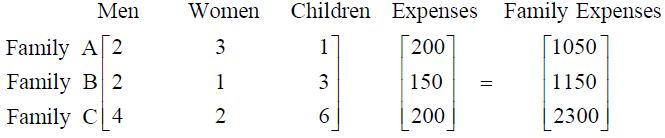
So expenses for family A, B and C are respectively 1050, 1150 and 2300 (in ₹).
Impact : More children in the family not only add to the expenses of the family but also add extra burden on the resources of the society.
8. If tan-1 x + tan-1 y + tan-1 z = π/2 ; x , y, z > 0 , then find the value of xy + yz + zx .
Solution: We have tan-1 x + tan-1 y + tan-1 z = π/2 ⇒ tan-1 x+y/1-xy = π/2 – tan-1 z = cot-1 z
⇒ tan-1 x+y/1-xy = tan-1 1/z ⇒ x+y/1-xy = 1/z
⇒ zx + yz = 1 – xy ∴ xy+ yz + zx = 1.
9. If a ≠ b ≠ c and

then using properties of determinants, prove that a + b + c = 0 .
Solution:

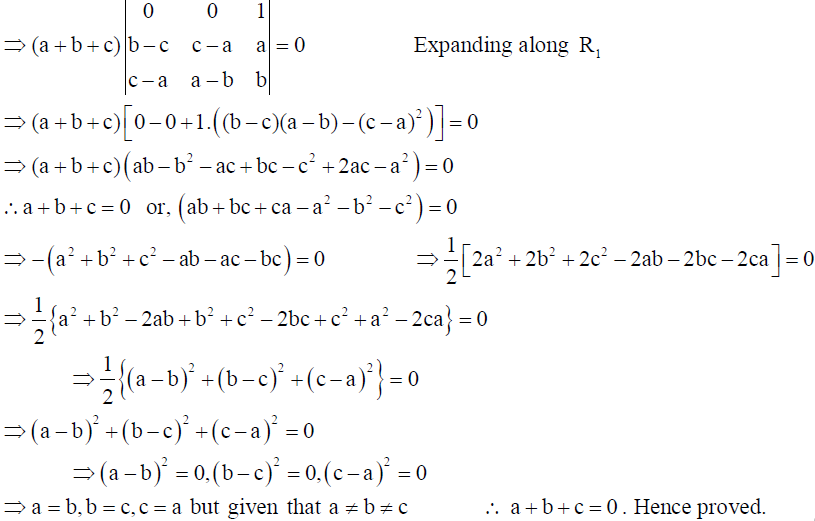
10. If
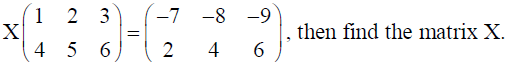
Solution:
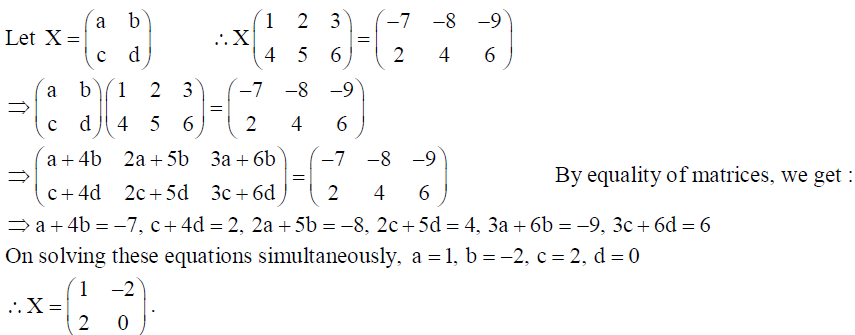
OR
Find the inverse of matrix
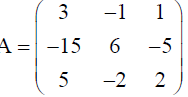
and hence show that A-1 . A = I .
Solution:

Hence A-1. A = I .
11. If function f (x) = |x – 3| + |x – 4|, then show that f (x) is not differentiable at x = 3 and x = 4. 11
Solution:
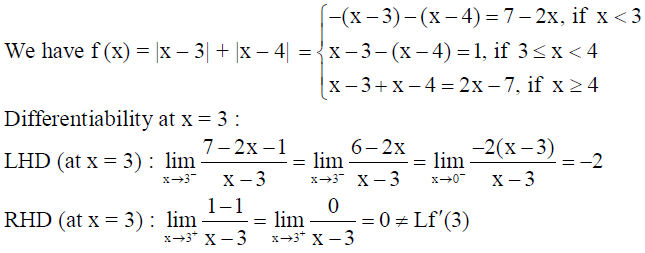
∴ (x) is not differentiable at x = 3.
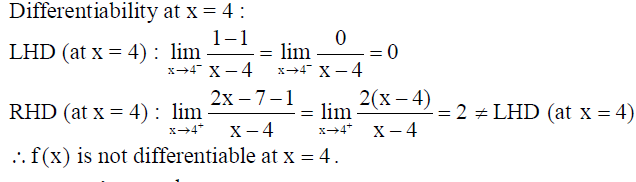
12. If y = xe-x2 , find dy/dx .
Solution:
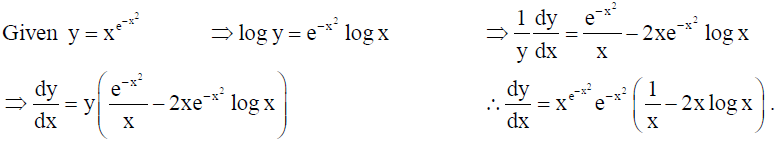
OR
If log √x2+y2 = tan-1(x/y) , then show that dy/dx = y-x/y+x .
Solution:

13. If y = √x+1 – √x-1 , prove that (x2-1) d2y/dx2 + x dy/dx – 1/4 y = 0 .
Solution:
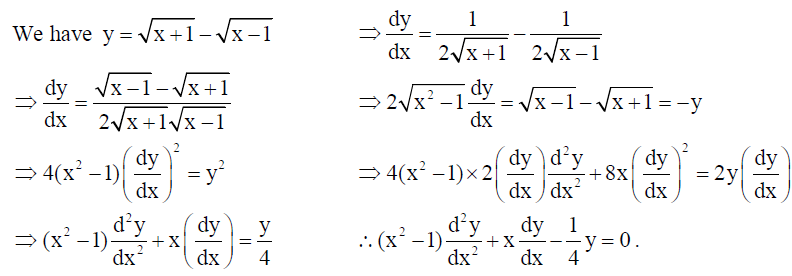
14. Find :
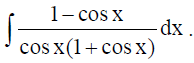
Solution:
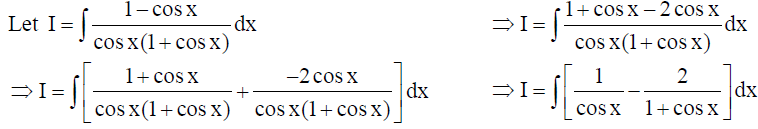
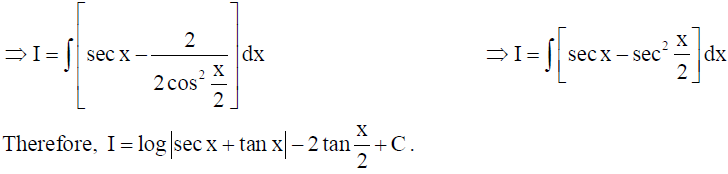
15. Evaluate : ∫ x sin-1 xdx .
Solution:
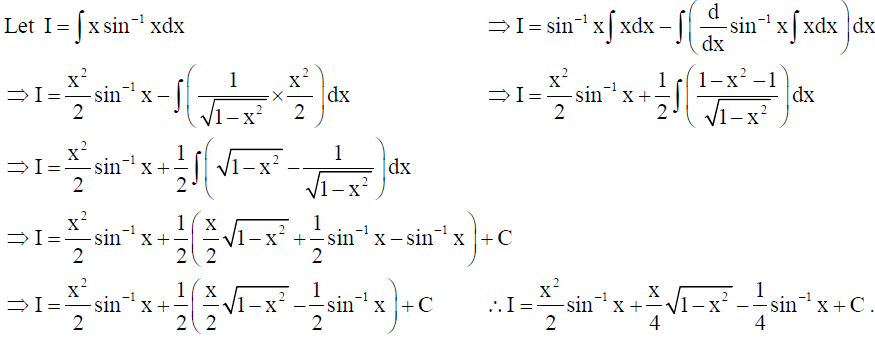
16.
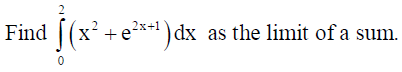
Solution:

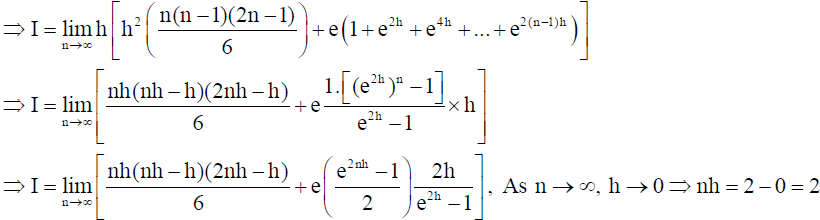

OR
Evaluate :
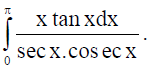
Solution:

17. Show that the lines x-1/3 = y-1/-1 , z+1 = 0 and x-4/2 = z+1/3 , y = 0 intersect each other. Also find their point of intersection.
Solution: Let L1 : x-1/3 = y-1/-1 , z+1 = 0 ⇒ x-1/3 = y-1/-1 = z+1/0 = λ
And L2 : x-4/2 = z+1/3 , y = 0 ⇒ x-4/2 = y/0 = z+1/3 = μ
Coordinates of random points on these lines are respectively P(3λ +1,-λ +1,-1) and Q(2μ + 4,0,3μ -1) .
When the lines L1 and L2 intersect each other, points P and Q must coincide i.e.,
3λ +1 = 2μ + 4…(i),-λ + 1= 0…(ii),-1= 3μ -1…(iii) ⇒ 3λ – 2μ = 3…(i),λ =1…(ii),μ = 0…(iii)
Solving (ii) and (iii) we get λ =1, μ = 0 .
Replacing value of λ =1, μ = 0 in LHS of (i) : 3λ – 2μ = 3×1- 2×0 = 3 = RHS of (i)
Hence lines L1 and L2 are intersecting.
Also the point of intersection is P or Q (4, 0, –1).
18. Let P(3, 2, 6) be a point in the space and Q be a point on the line r̅ = (î – ĵ + 2k̂) + μ (- 3î + ĵ + 5k̂) , then find the value of μ for which the vector P̅Q̅ is parallel to the plane x – 4y + 3z =1.
Solution: Since Q lies on r̅ = (î – ĵ + 2k̂) + μ (- 3î + ĵ + 5k̂) so, coordinates of Q (- 3μ + 1, μ – 1,5μ + 2) .
The direction ratios of line PQ : -3μ – 2 , μ – 3 , 5μ – 4 .

OR
Find the vector and Cartesian equations of the plane which bisects the line joining the points (3, –2, 1) and (1, 4, –3) at right angles.
Solution: The d.r.’s of the line joining the points (3, –2, 1) and (1, 4, –3) are 2, –6, 4 i.e., 1, –3, 2.
Also mid-point of this line is (2, 1, –1).
So the plane through (2, 1, –1) and perpendicular to a line with d.r.’s 1, –3, 2 is :
1(x – 2) – 3(y -1) + 2(z +1) = 0 i.e., x – 3y + 2z + 3 = 0 which is the Cartesian equation of plane.
And vector equation is r̅ = (î – 3ĵ + 2k̂) + 3 = 0
19. From a set of 100 cards numbered 1 to 100, one card is drawn at random. Find the probability that the number on the card is divisible by 6 or 8, but not by 24.
Solution: Total numbers which are divisible by 6 from 1 to 100 are 16, nos. which are divisible by 8 are 12 and the nos. which are divisible by 24 are 4.
∴ P(number is divisible by 6 but not by 24) = 16/100 – 4/100 = 12/100
and P(number is divisible by 8 but not by 24) = 12/100 – 4/100 = 8/100
Therefore, required probability = 12/100 + 8/100 = 20/100 or 1/5 .
SECTION – C
20. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b) : |a – b| is divisible by 2} is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other, but no element of {1, 3, 5} is related to any element of {2, 4}.
Solution: We have R = {(a, b) : | a – b | is divisible by 2} where a, b ∈ A and A = {1, 2,3,4,5} .
Reflexivity : For any a∈A , we have | a – a | = 0 , which is divisible by 2. That is, (a,a)∈ R so, R is reflexive.
Symmetry : Let (a, b)∈ R ∀ a,b∈A . We have | a – b | is divisible by 2.
As | a – b | = | b – a | . So | b – a | is also divisible by 2. That is, (b, a)∈R so, R is symmetric.
Transitivity : Let a, b,c ∈ A such that (a, b)∈ R and (b,c)∈ R then, | a – b | is divisible by 2 and | b – c | is divisible by 2.
This implies that | a – b | = 2m and | b – c |= 2p where m,p∈Z .
As (a – b) + (b – c) = ±2(m + p) ⇒ a – c = ±2(m+ p) ⇒| a – c |= 2(m+ p) .
That is, | a – c | is also divisible by 2 so, R is transitive.
Since the relation R is reflexive, symmetric and transitive so, it is an equivalence relation.
In the relation R all the elements corresponding to {1, 3, 5} are related to each other i.e., (1,3), (3,1), (1,5), (5,1), (3,5), (5,3). Also, all the elements of {2, 4} are related to each other as well since their difference is even (divisible by 2). But no element of {1, 3, 5} is related to any element of {2, 4} because the difference of elements of two sets is not even (not divisible by 2).
21. Using integration, find the area bounded by the curves y = | x – 1 | and y = 3 – | x |.
Solution: Given curves are
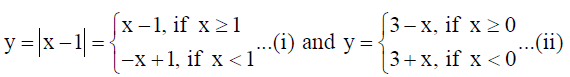
When curves (i) and (ii) intersect each other in I quadrant, x -1= 3- x ⇒ x = 2 ∴ (2, 1)
When curves (i) and (ii) intersect each other in II quadrant, 1- x = 3 + x ⇒ x = -1 ∴ ( -1, 2) .

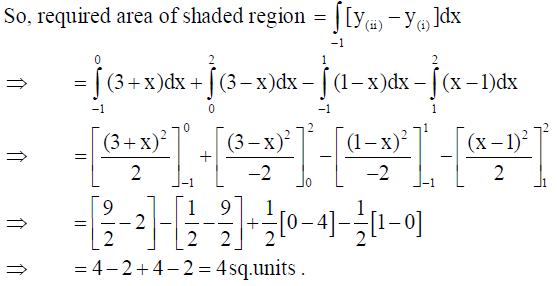
22. Find the point on the curve y = x/1+x2 , where the tangent to the curve has the greatest slope.
Solution:
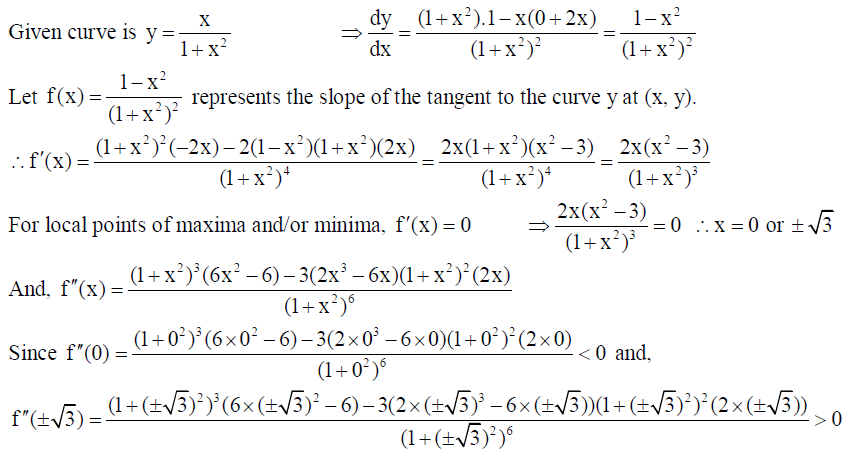
∴ x = 0 is point of local maxima.
Replacing value of x in the given curve, y = 0/1+02 = 0
Therefore, the required point is (0,0) .
23. Find the general solution of the differential equation dy/dx = y2/xy-x2 .
Solution:

OR
Solve the following differential equation, given that y = 0 , when x = π/4 :
sin2x dy/dx – y = tan x .
Solution:
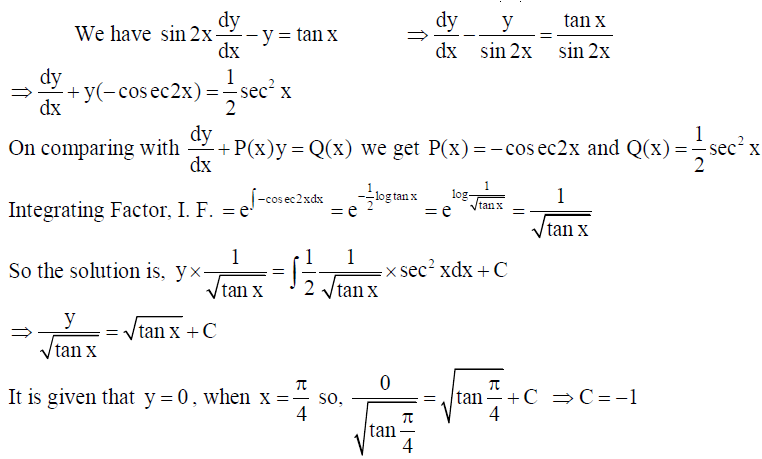
Therefore the required solution is y/√tan x = √tan x – 1 i.e., y = tan x – √tan x .
24. Find the vector and cartesian equations of the plane passing through the intersection of the planes r̅ .(î + ĵ + k̂) = 6 and r̅ .(2î + 3ĵ + 4k̂) = -5 and the point (1, 1, 1).
Solution:
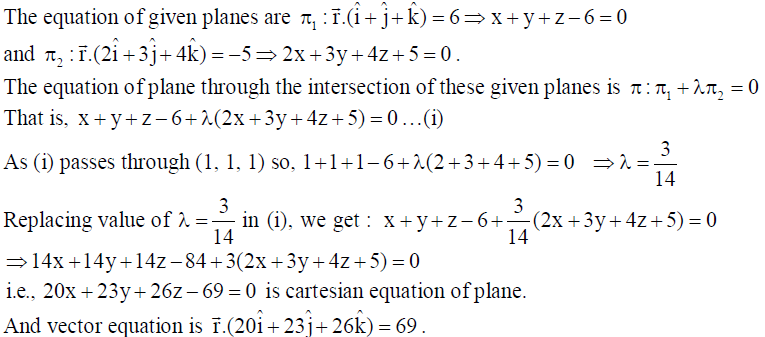
25. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduces the risk of heart attack by 30% and the prescription of a certain drug reduces its chance by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga.
Solution: Let A be the event that the patient follows a course of meditation and yoga, B be the event that
he takes a certain drug.
Then, P(A) = 1/2, P(B) = 1/2.
Let E be the event that the patient suffers a heart-attack.
Also P(E|A) = 70/100 x 40/100 , P(E|B) = 75/100 x 40/100
By Bayes’ Theorem, we get :
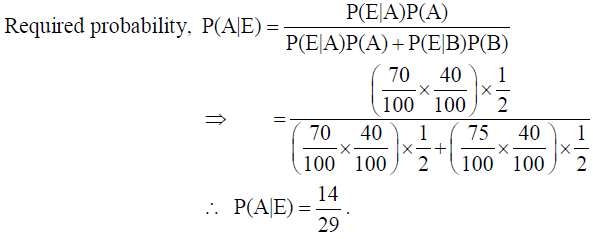
26. A dealer deals in two items only – item A and item B. He has ₹ 50,000 to invest and a space to store at most 60 items. An item A costs ₹ 2,500 and an item B costs ₹ 500. A net profit to him on item A is ₹ 500 and on item B ₹ 150. If he can sell all the items that he purchases, how should he invest his amount to have maximum profit ? Formulate an LPP and solve it graphically.
Solution: Let the number of items in item A and B respectively be x and y.
To maximize : z = ₹ (500x + 150y)
Subject to the constraints : x + y ≤ 60, 2500x + 500y ≤ 50000 i.e., 5x + y ≤100, x ≥ 0, y ≥ 0 .
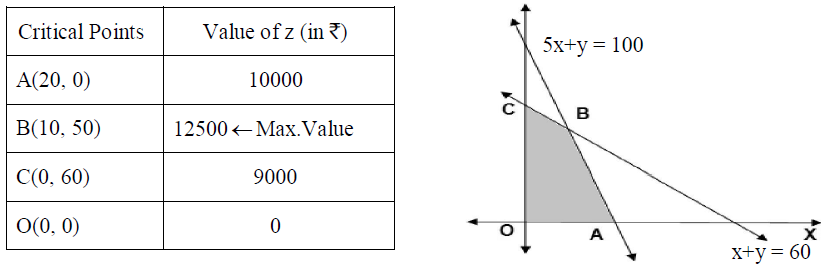
Therefore the maximum profit of ` 12500 is obtained for 10 and 50 items of item A and item B respectively.
OR
A dietician wants to develop a special diet using two foods X and Y. Each packet (contains 30 g) of food X contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Y contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires at least 240 units of calcium, at least 460 units of iron and at most 300 units of cholesterol. Make an LPP to find how many packets of each food should be used to minimise the amount of vitamin A in the diet, and solve it graphically.
Solution: Let the number of packets of food X and Y respectively be x and y.
To minimize : z = (6x + 3y) units
Subject to the constraints : 12x + 3y ≥ 240, 4x + 20y ≥ 460, 6x + 4y ≤ 300, x ≥ 0, y ≥ 0
or 4x + y ≥ 80, x + 5y ≥115, 3x + 2y ≤ 150, x ≥ 0, y ≥ 0 .

Therefore the minimum amount of vitamin A is 150 units for 15 and 20 packets of food X and food Y respectively.
