Please refer to Class 12 Mathematics Sample Paper With Solutions Set A provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
PART – A
Section – I
1. Find the magnitude of the vector a = 3i − 2 j + 6k .
Answer : Here, a = 3i − 2 j + 6k
∴ Its magnitude = |a|

OR
Find the number of vectors of unit length perpendicular to both the vectors a = 2i + j + 2k and b = j + k .
Answer : Given, a =2i + j +2k and b = j + k
Unit vectors perpendicular to a and b are ±

So, there are two unit vectors perpendicular to the given vectors.
2. Suppose that five good fuses and two defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement. What is the probability that we are lucky and find both of the defective fuses in the first two tests?
Answer : Let D1, D2 be the events that we find a defective fuse in the first and second test respectively.
∴ Required probability = P(D1 ∩ D2)
= P(D1)P(D2|D1) = 2/7 . 1/6 = 1/21
3. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
Answer : For transitivity of a relation, if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
We have, R = {(1, 2), (2, 1)}
⇒ (1, 2) ∈ R and (2, 1) ∈ R but (1, 1) ∉ R
∴ R is not transitive.
OR
Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a – b)}. Write the equivalence class [0].
Answer : Here, R = {(a, b) ∈ A × A : 2 divides (a – b)}, which is an equivalence relation, where
A = {0, 1, 2, 3, 4, 5}.
Clearly, [0] = {a ∈ A : aR0}
= {a ∈ A : 2 divides (a – 0)} = {a ∈ A : 2 divides a}
= {0, 2, 4}
∴ Equivalence class [0] is {0, 2, 4}.
4. Find the direction cosines of the line (4-x)/2 = y/6 = 1-z/3
Answer : The given equation of line is

5. If the matrix A =

is skew symmetric, then find the value of ‘a’ and ‘b’.
Answer : Since, matrix A is skew symmetric matrix.
∴ A′ = –A

From (i), A + A′ = O

∴ a + 2 = 0 and b –3 = 0
⇒ a = –2 and b = 3
OR
Write the element a23 of a 3 × 3 matrix A = [aij] whose elements aij are given by aij = |i – j| /2
Answer : Here, aij = |i-j| /2
∴ For i = 2, j = 3 we have, a23 = |2-3|/2 = |-1|/2 =1/2
6. If

= 8 , then find the value of x.
Answer : Expanding the given determinant, we get
x(–x2 – 1) –sin θ(–xsin θ – cos θ) + cos θ (–sin θ + xcos θ) = 8
⇒ –x3 – x + x = 8
⇒ x3 + 8 = 0
⇒ (x + 2) (x2 – 2x + 4) = 0
⇒ x + 2 = 0 [ ∵ x2 – 2x + 4 > 0 ∀x]
⇒ x = –2
7. Find the value of

Answer : We have,

OR
Evaluate :

Answer :

Put x2 + 1 = t ⇒ 2xdx = dt ⇒ xdx = 1/2dt
Also x = 2 ⇒ t = 5 and x = 4 ⇒ t = 17
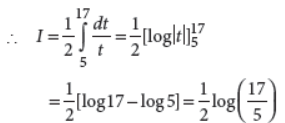
8. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B, state whether f is one-one or not.
Answer : We have, A = {1, 2, 3}, B = {4, 5, 6, 7} and
f = {(1, 4), (2, 5), (3, 6)}
∴ f(1) = 4, f(2) = 5 and f(3) = 6.
Since, distinct elements of A have distinct images in B, therefore, f is one-one function.
9. If a line makes an angle Θ1, Θ2 and Θ3 with the x, y and z-axes respectively, then find the value of cos 2Θ1 + cos 2Θ2 + cos 2Θ3.
Answer : Consider, cos2θ1 + cos 2θ2 + cos2θ3
= 2(cos2θ1+ cos2θ2 + cos2θ3) – 3 ( cos2x = 2cos2 x – 1)
= 2(1) – 3 = – 1
OR
If the equation of a line AB is x-3 / 1 = y+2/-2 = z-5/4 , then find the numbers to which direction ratios of a line parallel to AB, are proportional.
Answer : Since direction ratios of line AB are 1, –2, 4, therefore the direction ratios of line parallel to AB will be proportional to 1, –2 and 4.
10. Find the order and degree of y = px + √(a2p2+b2) , where p = dy/dx
Answer : Given, y − px = √(a2p2 + b2)
⇒ (y – px)2 = a2p2 + b2
⇒ (x2 – a2)p2 – 2xyp + (y2 – b2) = 0

11. Find the area enclosed by the ellipse x2/a2 + y2/b2 = 1.
Answer : We know that, the area enclosed by ellipse
x2/a2 + y2/b2 = 1 is πab sq. units.
12. Find the sum of the vectors
a = i − 2 j + k,
b = −2i + 4j + 5k = and c = i – 6j – 7k
Answer : The given vectors are
The given vectors are
a = î − 2 ĵ + k̂, b = −2î + 4 ĵ + 5k̂ ,
c = i − 6 ĵ − 7k̂
∴ Required sum = a + b + c
= (î − 2ĵ + k̂) + (−2î + 4ĵ + 5k̂) + (î − 6ĵ − 7k̂) = −4ĵ − k̂.
13. Check whether the relation R in the set R of real numbers defined as R = {(a, b) : a < b} is (i) symmetric, (ii) transitive.
Answer : We have, R = {(a, b) : a < b}, where a, b ∈ R
(i) Symmetric : Let (x, y) ∈ R, i.e., x R y ⇒ x < y
Then, y x, so (x, y) ∈ R ⇒ (y, x) ∉ R
Thus, R is not symmetric.
(ii) Transitive : Let (x, y) ∈ R and (y, z) ∈ R
⇒ x < y and y < z ⇒ x < z
⇒ (x, z) ∈ R. Thus, R is transitive.
14. If A is a square matrix such that A2 = A, then show that (I – A)3 + A = I.
Answer : We have, A2 = A
Now, L.H.S. = (I – A)3 + A = (I – A)(I – A)(I – A) + A
= (I ⋅ I – I ⋅ A – A ⋅ I + A ⋅ A)(I – A) + A
= (I – A – A + A)(I – A) + A
[∵ I ⋅ A = A ⋅ I = A and A2 = A]
= (I – A)(I – A) + A
= (I ⋅ I – I ⋅ A – A ⋅ I + A ⋅ A) + A
= (I – A – A + A) + A = (I – A) + A = I = R.H.S.
Hence, (I – A)3 + A =I
15. Find the value of P(A ∪ B), if 2P(A) = P(B) = 5/13 and P(A | B) = 2/5
Answer : Given, P(A|B) = 2/5 ⇒ P(A∩B) /P (B) = 2/5

16. If (a ×b)2 + (a,b) = 400 and |a| = 4, then find |b|.
Answer : We hāve, (ā ×Ђ) + (ā.Ђ)2 = 400 ānd 4
We know thāt,
(ā ×Ђ) + (ā.Ђ) = |ā|2 |Ђ|2
⇒ 400 = (4)2 |Ђ|2 ⇒ 16|Ђ|2 = 400
⇒ |Ђ|2 = 25 ⇒ |Ђ| = 5
Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. Neelam and Ved appeared for first round of an interview for two vacancies. The probability of Neelam’s selection is 1/6 and that of Ved’s selection is 1/4.
Answer : Let A be the event that Neelam is selected and B be the event that Ved is selected. Then, we have,
P(A) = 1/6
⇒ P(A) = 1-1/6 = 5/6 = p (Neelam is not selected)
P(B) = 1/4
⇒ P(B) = 1-1/4 = 3/4 = P (Ved is not selected)
Based on the above information, answer the following questions :

(i) The probability that both of them are selected, is
(a) 1/12
(b) 1/24
(c) 1/6
(d) 1/2
Answer : B
(ii) The probability that none of them is selected, is
(a) 2/7
(b) 3/8
(c) 5/8
(d) 1/3
Answer : C
(iii) The probability that only one of them is selected, is
(a) 5/8
(b) 2/3
(c) 2/7
(d) 1/3
Answer : D
(iv) The probability that atleast one of them is selected, is
(a) 3/8
(b) 1/8
(c) 3/7
(d) 2/7
Answer : A
(v) Suppose Neelam is selected by the manager and told her about two posts P and Q for which selection is independent. If the probability of selection for post P is
1/6 and for post Q is 1/7 , then the probability that Neelam is selected for at least one post, is
(a) 1/7
(b) 2/7
(c) 3/8
(d) 1/2
Answer : B
18. Sonam wants to prepare a sweet box for Diwali at home. For making lower part of box, she takes a square piece of cardboard of side 18 cm.

Based on the above information, answer the following questions :
(i) If x cm be the length of each side of the square cardboard which is to be cut off from corner of the square piece of side 18 cm, then x must lie in
(a) [0, 18]
(b) (0,9)
(c) (0, 3)
(d) None of these
Answer : B
(ii) Volume of the open box formed by folding up the cutting corner can be expressed as
(a) V = x(18 – 2x)(18 – 2x)
(b) V = x/2 (18 + x)(18 – x)
(c) V = x/3 (18 – 2x)(18 + 2x)
(d) V = x(18 – 2x)(18 – x)
Answer : A
(iii) The values of x for which dV/dx = 0, are
(a) 3, 2
(b) 0, 3
(c) 0, 9
(d) 3, 9
Answer : D
(iv) Sonam is interested in maximising the volume of the box. So, what should be the side of the square to be cut off so that the volume of the box is maximum?
(a) 13 cm
(b) 8 cm
(c) 3 cm
(d) 2 cm
Answer : C
(v) The maximum value of the volume is
(a) 144 cm3
(b) 232 cm3
(c) 256 cm3
(d) 432 cm3
Answer : D
PART – B
Section – III
19. Differentiate sin2 x w.r.t. ecos x.
Answer : Let u(x) = sin2 x and v(x) = ecos x.
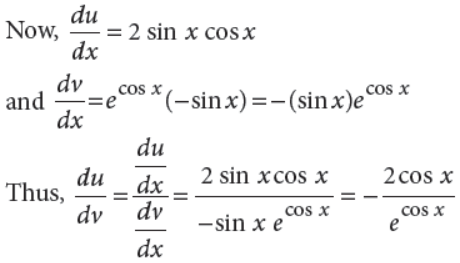
20. Find

Answer :

OR
Evaluate :

Answer :

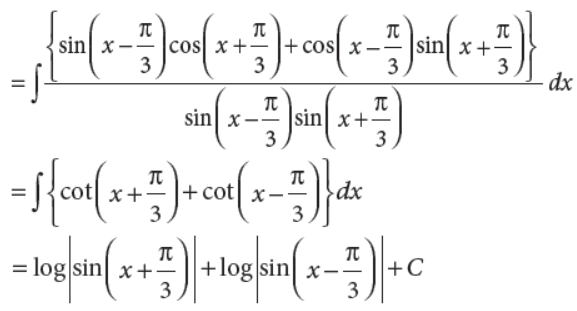
21. Prove that the area enclosed between the x-axis and the curve y = x2 – 1 is 4/3 sq. units
Answer : The equation y = x2 – 1 represents a upward parabola with vertex at (0, –1).
It cuts x-axis where y = 0
i.e., x2 – 1 = 0 ⇒ x = ± 1

22. Find the value of cos-1 (1/2) + 2sin-1 (1/2)
Answer : We know that the range of principal value branch of cos–1 and sin–1 are [0, π] and [-π/2 , π/2] respectively.

23. If ā = 2i + 3j − k and Ђ = i + 2j + 3k , find a ×b and | ā ×Ђ |.
Answer : GIven,
ā = 2î + 3ĵ − k̂ and b = î + 2 ĵ + 3k̂

OR
Prove by vector method that the area of △ABC is a2 sin B sin C / 2 sin A
Answer : Area of the triangle ABC


24. If A and B are events such that P(A) = 1/3 , P(B) = 1/4 and P(A ∩ B) = 1/12 , then find P(not A and not B).
Answer : Here, P(A) . P(B) = 1/3 x 1/4 = 1/12 = P(A∩B)
⇒ Events A and B are independent.
⇒ Events A and B are also independent.
Now, P(A ∩ B) = P(A) P(B)
( ∵ A and B are independent events)
= (1 – P(A))(1 – P(B))
= (1-1/3)(1-1/4) = 2/3 x 3/4 = 1/2
25. Show that the function f(x) = 4x3 – 18x2 + 27x – 7 is always increasing on R.
Answer : We have, f(x) = 4x3 – 18x2 + 27x – 7
⇒ f ′(x) = 12x2 – 36x + 27

Hence, f(x) is always increasing on R.
26. If the solution of the differential equation dy/dx = ax + 3/2y + f represents a circle, then find the value of ‘a’.
Answer : We have,

[ coefficient of x2 should be equal to coefficient of y2]
27. Find the vector equation of the line passing through the point A(1, 2, –1) and parallel to the line 5x – 25 = 14 – 7y = 35z.
Answer : Vector equation of the line passing through (1, 2, –1) and parallel to the line
5x – 25 = 14 – 7y = 35z
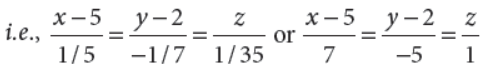
î s r̂ = (î + 2 ĵ − k̂)+ λ(7î − 5ĵ + k̂)
28. If A is a non-singular 3 × 3 matrix such that |5 ⋅ adjA| = 5, then find |A|.
Answer : Given that |5 adjA| = 5 and
A is non-singular matrix, i.e., |A| ≠ 0.
Clearly, |5 adjA| = 5

OR
If there are two values of a which makes determinant, △ =

= 86 , then find the sum of these values.
Answer :

Expanding along C1, we get
1(2a2 + 4) – 2(–4a – 20) = 86
⇒ 2a2 + 4 + 8a + 40 = 86
⇒ 2a2 + 8a – 42 = 0
⇒ a2 + 4a – 21 = 0 ⇒ (a + 7)(a – 3) = 0 ⇒ a = 3, –7
Now, sum of values of a is 3 + (–7) = 3 – 7 = –4
Section – IV
29. Find the value of k, for which
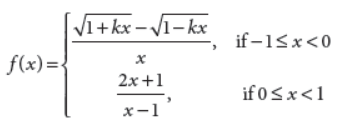
is continuous at x = 0.
Answer : Since, f(x) is continuous at x = 0

Now, from (i), (ii), (iii) and (iv), we get k = –1
30. Evaluate :

Answer :


31. Differentiate the function log (a+b sinx / a-b sinx) with respect to x.
Answer : Let
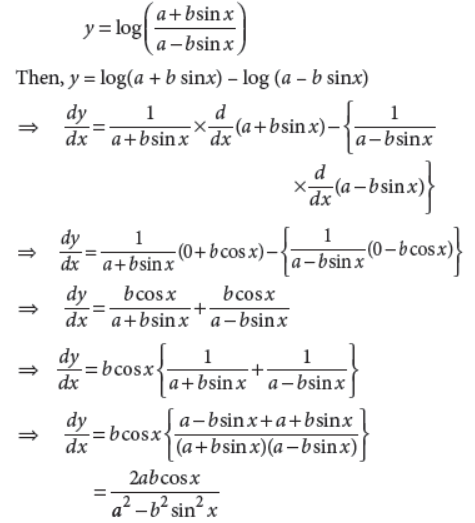
OR
Find dy/dx ,when y = √a+√a+√a+x2 , where a is a constant.
Answer :

32. Find area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle
x2 + y2 = 32.
Answer : We have, x2 + y2 = 32 …(i), a circle with centre (0, 0) and radius 4 2, and y = x …(ii), a straight line.
Solving (i) and (ii), we get point of intersection (4, 4) in the first quadrant.

33. If the equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x –5, then find the values of a and b.
Answer : We have, y2 = ax3 + b
Differentiating w.r.t. x, we get

So, equation of tangent at the point (2, 3) is
y – 3 = 2a (x – 2)
⇒ y = 2ax – 4a + 3 …(i)
But we are given that equation of tangent at (2, 3) is
y = 4x – 5 …(ii)
∴ On comparing (i) and (ii), we get
2a = 4 ⇒ a = 2
∵ Point (2, 3) lies on the curve y2 = ax3 + b,
∴ (3)2 = (2)3 a + b ⇒ 9 = 8a + b
⇒ 9 = 8 × 2 + b ⇒ b = –7
34. Solve the differential equation :
(1 + x2) dy/dx +2xy-4x2 = 0 subject to the initial condition y(0) = 0.
Answer : We have,


OR
Find the particular solution of the differential equation dy/dx = x(2logx+1) / sin y + y cos y , given that y = π/2 , when x = 1.
Answer :

35. Show that the function f : (–∞, 0) → (–1, 0) defined by f(x) = x / 1 +|x| , x ∈ (–∞, 0) is one-one and onto.
Answer :

Here, y ∈ (–1, 0)
So, x is defined for all values of y.
Also x ∈ (–∞, 0) for all y ∈ (–1, 0).
∴ f is onto.
Section – V
36. Find the inverse of the matrix A =

Answer : We have,
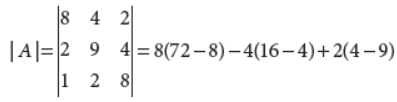
= 512 – 48 – 10 = 454 ≠ 0
Thus, A is a non-singular matrix and therefore it is invertible.
Let Cij be cofactor of aij in A. Then,

OR
If A=

, verify that (AB)–1 = B–1 A–1.
Answer :

From (i) and (ii), (AB)–1 = B–1 A–1.
37. Find the equation of the plane passing through the points (2, 2, –1) and (3, 4, 2) and parallel to the line whose direction ratios are 7, 0, 6.
Answer : The equation of a plane passing through (2, 2, –1) is a(x – 2) + b(y – 2) + c(z + 1) = 0 …(i)
This plane also passes through (3, 4, 2).
∴ a(3 – 2) + b(4 – 2) + c(2 + 1) = 0
⇒ a + 2b + 3c = 0 …(ii)
Now, plane (i) is parallel to the line whose direction ratios are 7, 0, 6
Therefore, 7a + 0(b) + 6c = 0
Solving (ii) and (iii) by cross-multiplication method,
we get
a /(2) (6) − (0) (3) = b/(7) (3) (6) (1) = c/(0)(1) (2) (7)
⇒ a/12 = b/15 = c/-14 = λ (say)
⇒ a = 12l, b = 15l, c = –14l
Substituting the values of a, b, c in (i), we get
12λ(x – 2) + 15λ(y – 2) – 14λ(z + 1) = 0
⇒ 12x – 24 + 15y – 30 – 14z – 14 = 0 [∵ λ ≠ 0]
⇒ 12x + 15y – 14z = 68
This is the required equation of plane.
OR
Consider the lines L1 : (x+1)/3 = (y+2)/1 = (z+1)/2 , L2 : (x-2)/1 = (y+2)/2 = (z-3)/3
Find the distance of the point (1, 1, 1) from the plane passing through the point (–1, –2, –1) and whose normal is perpendicular to both the lines L1 and L2.
Answer : Any plane through (–1, –2, –1) is
a(x + 1) + b(y + 2) + c(z + 1) = 0 …(i)
D.R.’s of any normal to (i) are < a, b, c >.
As this normal is perpendicular to both L1 and L2,
therefore,
3a + 1b + 2c = 0 …(ii)
1a + 2b + 3c = 0 …(iii)
Eliminating a, b, c between (i), (ii) and (iii), we obtain
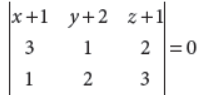
⇒ (x + 1)(3 – 4) – (y + 2)(9 – 2) + (z + 1)(6 – 1) = 0
⇒ – (x + 1) – 7 (y + 2) + 5 (z + 1) = 0
or x + 7y – 5z + 10 = 0 …(iv)
This is the required equation of plane.
∴ Distance of (1, 1, 1) from the plane (iv)

38. Solve the following LPP graphically.
Maximize, Z = 150x + 250y
Subject to the constraints
x + y ≤ 35
1000x + 2000y ≤ 50000
x, y ≥ 0
Answer : The given problem is
Maximize , Z = 150x + 250y
Subject to the constraints
x + y ≤ 35, x + 2y ≤ 50 and x, y ≥ 0
To solve graphically, we convert the inequations into
equations to obtain the following lines :
x + y = 35, x + 2y = 50, x = 0, y = 0
Let us draw the graph of these lines as shown below.

The feasible region is the shaded region. We observe that the region is bounded.
The corner points of the feasible region OBED are
O(0, 0), B(35, 0), E(20, 15) and D(0, 25).
The value of the objective function at corner points of the feasible region are :
| Corner points | Value of Z = 150x + 250y |
| O(0, 0) | 0 |
| B(35, 0) | 5250 |
| E(20, 15) | 6750 (Maximum) |
| D(0, 25) | 6250 |
Clearly, Z is maximum at x = 20, y = 15.
OR
Find the number of point(s) at which the objective function Z = 4x + 3y can be minimum subjected to the constraints 3x + 4y ≤ 24, 8x + 6y ≤ 48, x ≤ 5, y ≤ 6; x, y ≥ 0.
Answer : Let l1 : 3x + 4y = 24, l2 : 8x + 6y = 48, l3 : x = 5,
l4 : y = 6, l5 : x = 0, l6 : y = 0
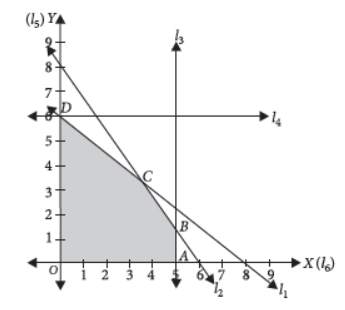
For B : Solving l2 and l3, we get B(5, 4/3)

Thus, Z is minimum at 1 point O(0, 0).
