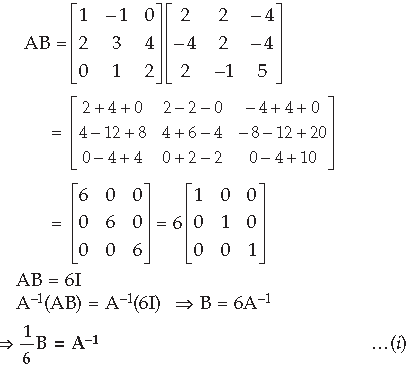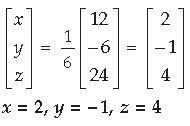Students can read the important questions given below for Determinants Class 12 Mathematics. All Determinants Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Determinants Class 12
Very Short Answer Type Questions
Question. If A is an invertible matrix of order 3 and |A| = 5, then find |Adj A|.
Answer.
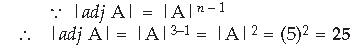
Question. If A is a non-singular matrix of order 3 and |Adj A| = |A|K, then write the value of K.
Answer.

Question. If A is a square matrix of order 3 and |3A| = K|A|, then write the value of K.
Answer.
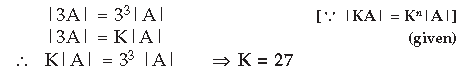
Question. A is a square matrix of order 3 and |A| = 7. Write the value of |adj. A|.
Answer. |adj. A|= |A|n–1
= |A|3 – 1 = (7)2 = 49
Question. If |A| = 2, where A is a 2 × 2 matrix, find |adj A|.
Answer. |adj A|= |A|n – 1 = (2)2 –1 = 2
Question. What is the value of the determinant
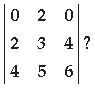
Answer. Expanding along R1 = – 2(12 – 16) = – 2(– 4) = 8
Question. Find the minor of the element of second row and third column (a23) in the following determinant :
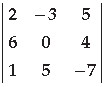
Answer.
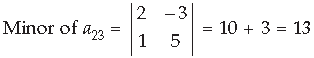
Question. What positive value of x makes the following pair of determinants equal?
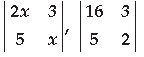
Answer.
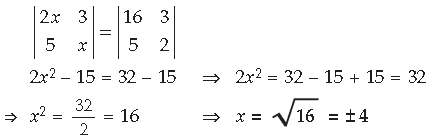
Question. Write the adjoint of the following matrix :
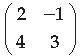
Answer.
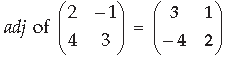
Question.
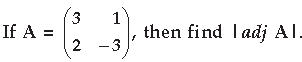
Answer.
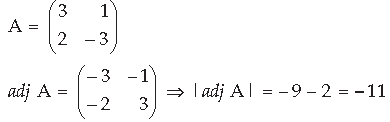
Question. A matrix A of order 3 × 3 is such that |A| = 4.
Find the value of |2A|.
Answer. |2A| = 2n|A| = 23(4) = 32
Question. If A is an invertible matrix of order 3 and |A| = 5, then find the value of |adj A|.
Answer. |adj A|= |A|n – 1
= (5)3–1 = (5)2 = 25
Question.

Answer.
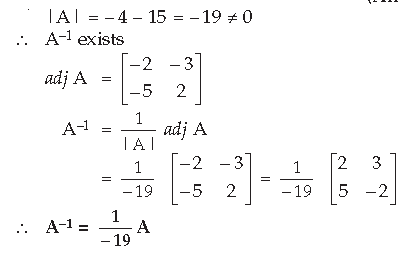
Question.
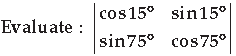
Answer.
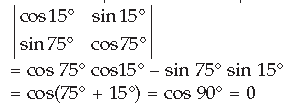
Question.
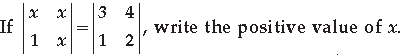
Answer.
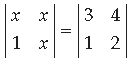
⇒ x2 – x = 6 – 4
⇒ x2 – x = 2
⇒ x2 – x – 2 = 0
⇒ x2 – 2x + x – 2 = 0
⇒ x(x – 2) + 1(x – 2) = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2 or x = – 1
∴ The positive value of x is 2.
Question. Let A be a square matrix of order 3 × 3. Write the value of |2A|, where |A| = 4.
Answer. |2A| = 23|A| = 8(4) = 32
Question. The value of the determinant of a matrix A of order 3 × 3 is 4. Find the value of |5A|.
Answer. |A| = 4
|5A| = 53 |A| = 125 (4) = 500
Question. If the determinant of a matrix A of order 3 × 3 is of value 4, write the value of |3A|.
Answer. |A| = 4
⇒ |3A| = 33 |A| = 27(4) = 108
Question.

Answer.
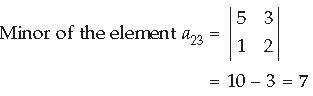
Question. If A is a square matrix of order 3 such that |adj A| = 64, find |A|.
Answer. |adj A| = 64
|A|2 = 64 [ ∵ |adj A| = |A|n–1, Here n= 3]
∴ |A| = ± 8
Question. If A is an invertible square matrix of order 3 and |A| = 5, then find the value of |adj A|.
Answer. |adjA|= |A|n–1
= (5)3–1
= 52 = 25 [Here |A| = 5, n = 3
Question.
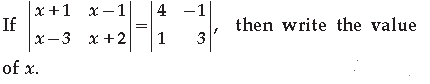
Answer. (x + 1) (x + 2) – (x – 1) (x – 3) = 12 + 1
⇒ (x2 + 2x + x + 2) – (x2 – 3x – x + 3) = 13
⇒ 3x + 2 + 4x – 3 = 13
⇒7x – 1 = 13 ⇒ 7x = 14
Question. If Aij is the cofactor of the element aij of the
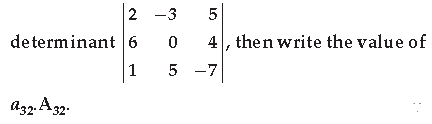
Answer.
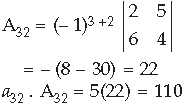
Question.
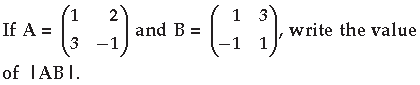
Answer.
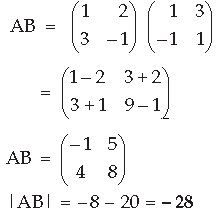
Question.
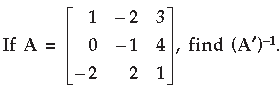
Answer.

Question. Find the inverse of the matrix
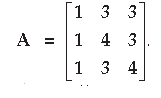
Answer.
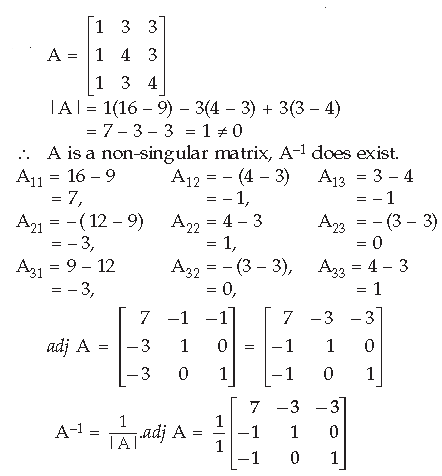
Question. Find the maximum value of
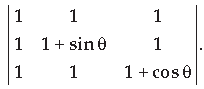
Answer.
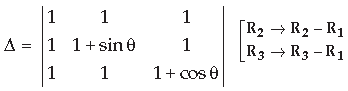
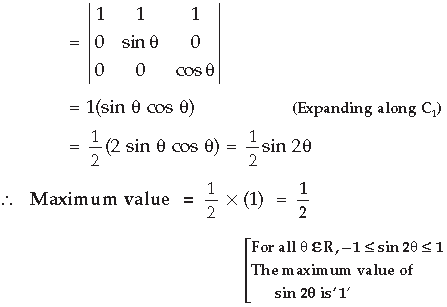
Question.
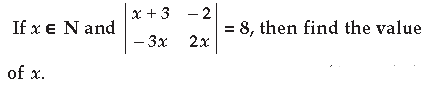
Answer.

Question. If A is a square matrix of order 2 and |adj A| = 9, find |A|.
Answer. |adj A|= 9 …(given)
|A|n – 1 = 9, (order, adj, n = 2)
|A|2 – 1 = 9
|A| = 9
Question. If for any 2 × 2 square matrix A,
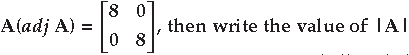
Answer.
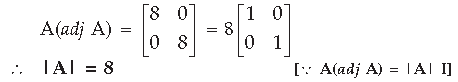
Question. If A is an invertible matrix of order 2 and det (A) = 4, then write the value of det (A–1).
Answer.
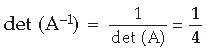
Question. If A is a 3 × 3 invertible matrix, then what will be the value of k if det(A–1) = (det A)k
Answer.

Short Answer Type Questions-I
Question. If A is a skew-symmetric matrix of order 3, then prove that det A = 0. (All India)
Answer. A is a skew-symmetric matrix
At = – A
⇒ |At| = |– A|
⇒ |At| = (– 1)n|A|
⇒ |At| = (– 1)3|A| …( ∵ = 3)
⇒ |A| = – |A| ( ∵ |At| = |A|)
⇒ |A| + |A| = 0
⇒ 2|A| = 0 ∴ |A| = 0
Short Answer Type Questions-II
Question.
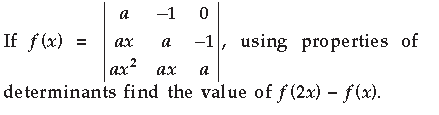
Answer. To find : f (2x) – f (x)
1st method :


Question. Using properties of determinants, prove the following :
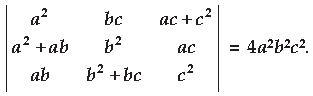
Answer.

Expanding along C1, we have
= – 2abc2 . 1(– ab – ab)
= – 2abc2 (– 2ab)
= 4a2b2c2 = R.H.S.
Question.

Answer.

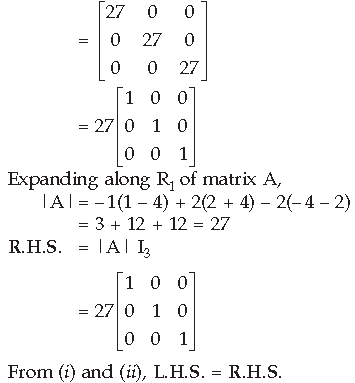
Question.
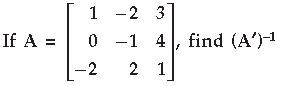
Answer.
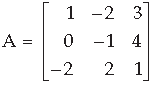
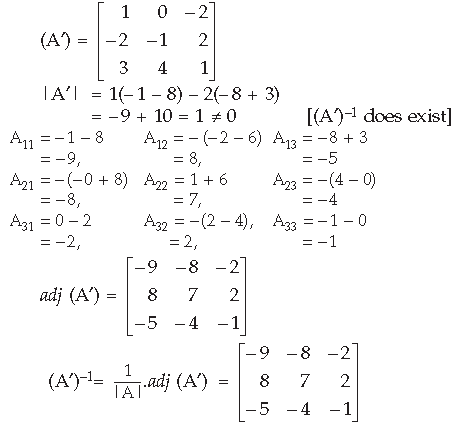
Question. Using properties of determinants, solve for x :
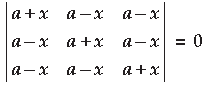
Answer.

Question. Two schools A and B decided to award prizes to their students for three values, team spirit, truthfulness and tolerance at the rate of ₹ x, ₹y and ₹ z per student respectively. School A, decided to award a total of ₹ 1,100 for the three values to 3, 1 and 2 students respectively while school B decided to award ₹ 1,400 for the three values to 1, 2 and 3 students respectively. If one prize for all the three values together amount to ₹ 600 then
(i) Represent the above situation by a matrix equation after forming linear equations.
(ii) Is it possible to solve the system of equations so obtained using matrices?
Answer.
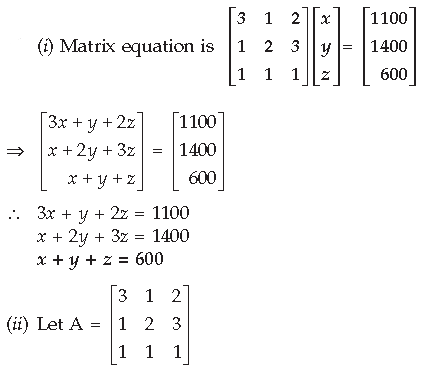
⇒ |A| = 3(2 – 3) – 1(1 – 3) + 2(1 – 2)
= – 3 + 2 – 2 = – 3 ≠ 0
A–1 exists, so equations have a unique solution. Hence system of equations can be solved.
Question. Using properties of determinants, prove that
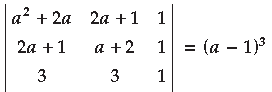
Answer.

Question.
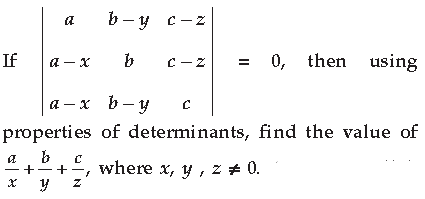
Answer.
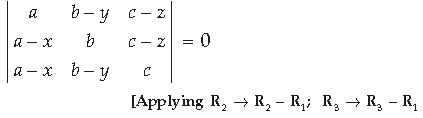
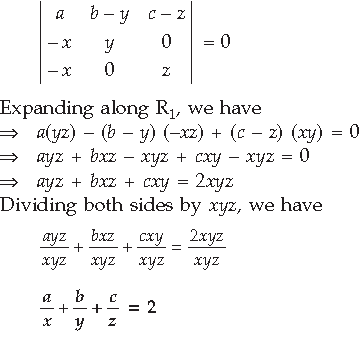
Question.
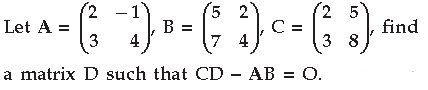
Answer. Given : CD – AB = 0
DC = AB ⇒ D = C–1AB …(i)
|C| = 16 – 15 = 1 ≠ 0;
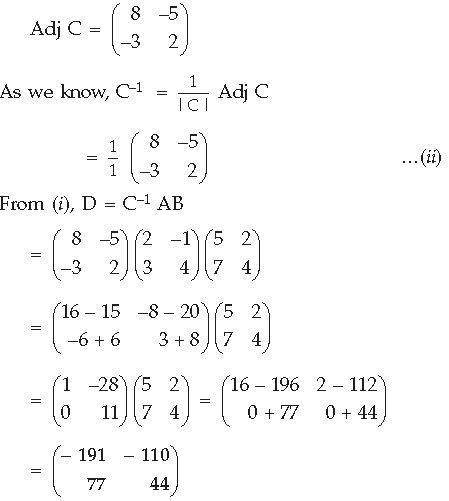
Long Answer Type Questions
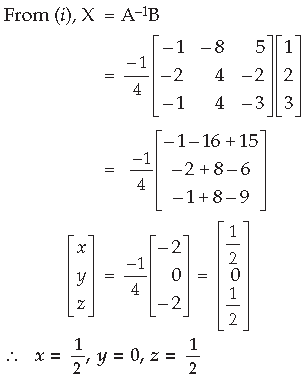
Question. Using matrices, solve the following system of equations :
x + y + z = 1;x – 2y + 3z = 2; x – 3y + 5z = 3
Answer. Given equations can be written as

Question. Using properties of determinants, show the following :
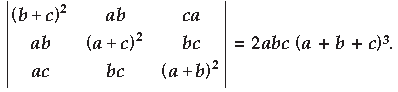
Answer.
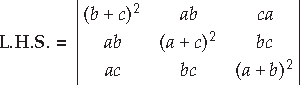


Question.
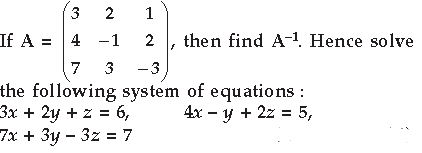
Answer.

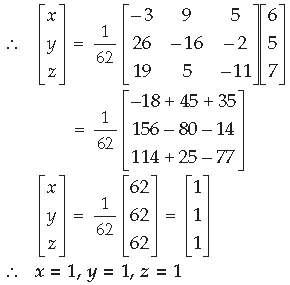
Question.
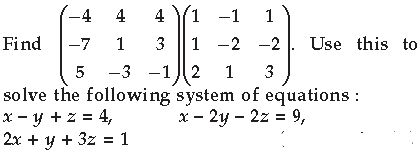
Answer. Part I :

Part II :
Given system of equations can be written in matrix form
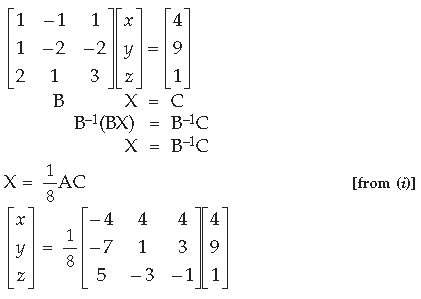
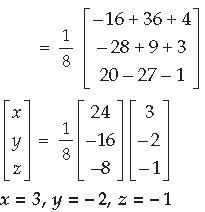
Question.
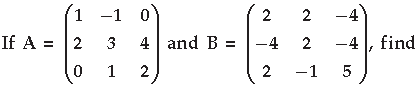
AB. Use this to solve the following system of equations :
x – y = 3, 2x + 3y + 4z = 17, y + 2z = 7
Answer. Part I :