Please refer to Class 12 Mathematics Sample Paper With Solutions Set I provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
Part–A
Section – I
All questions are compulsory. In case of internal choices attempt any one.
Q1. Check whether R be a relation on the set N defined by {(x, y): x, y ∈ N, 2x + y = 41} is transitive or not.
Answer : R is not transitive.
OR
Give an example of a relation which is transitive but neither reflexive nor symmetric.
Answer : {(2, 3), (2, 4), (4, 3)}
Q2. Let A = {1, 2, 3}. Write identity relation in A.
Answer : The set {(1, 1), (2, 2), (3, 3)} is the identity relation in A.
Q3. A relation R is defined from set A = {1, 3, 4, 5} to set B = {2, 4, 6} as: R = {(a, b) : b is divisible by a}, a ∈ A and b ∈ B. Write the relation R in roster form.
Answer : R = {(1, 2), (1, 4), (1, 6), (3, 6), (4, 4)}.
OR
If set A = {1, 2, 3, 4} and set B = {5, 6, 7, 8} and a relation R from set A to set B is defined as: R = {(a, b) : a + b = 5, a ∈ A, b ∈ B}. Is the relation R an empty relation? Give reason.
Answer : Yes, because a + b ≠ 5 for all a and b, where a ∈ A, b ∈ B
Q4. If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Answer : 1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6, 6 × 3; 1 × 5 and 5 × 1
Q5. If
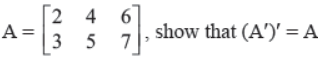
Answer : …….??
OR
If A

Answer : ……..?
Q6. Write the co-factors of elements of the second row of the determinant:

Answer : – 39, 3, 11
Q7. Find ∫sin 3x dx.
Answer : –cos 3x/3 + C
OR
Evaluate :
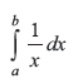
Answer : log b/a
Q8. Find the area of the region bounded by y2 = 9x, x=2, x=4 and the x-axis in the first quadrant.
Answer : (16 – 4 2 ) sq. units
Q9. Determine the order and degree of equation: 3d2y/dx2 – 5dy/dx + 2y = 0.
Answer : Order = 2, Degree = 1
OR
Show that y = x2 + 2x + C is a solution of differential equation y′ – 2x – 2 = 0.
Answer :
Q10. Find a̅.b̅ if a̅ = 3î – ĵ+2k̂ and b̅ = 2î + 3ĵ+3k̂.
Answer : 9
Q11. Write the scalar and vector components of position vector: r̅ = 4î – 5ĵ+7k̂.
Answer : Vector components: 4it, – 5tj, 7kt ; Scalar components: 4, – 5, 7
Q12. Compute the magnitude of vector:
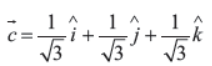
Answer : 1
Q13. Find the Cartesian equation of the plane r̅ = (î + ĵ– k̂) = 2.
Answer : x + y – z = 2
Q14. Find the vector equation of the plane: x + 2y + 2z = 5.
Answer : r̅ = (î + 2ĵ+ 2k̂) = 5
Q15. If P(A) = 5/3 and P(B) = 5/1 , find P(A ∩ B) if A and B are independent events.
Answer : 3/25
Q16. Compute P(A|B) if P(B) = 0.5 and P(A ∩ B) = 0.32.
Answer : 0.64
Section-II
Both the Case study-based questions are compulsory. Attempt any 4 sub-parts from each question (17–18). Each sub-part carries 1 mark.
Q17. Rahul buy some pepsi cans. All cans are of closed right cylindrical cans of volume 128 p cm3.
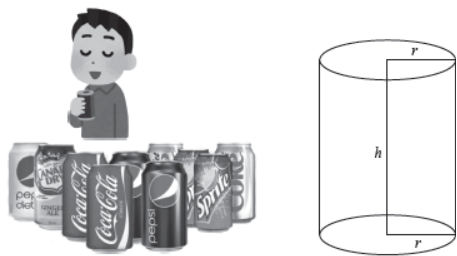
Based on the above information answer the following:
(i) Height of cylindrical can is
(a) 128/r2
(b) 182/r2
(c) 812/r2
(d) 821/r2
Answer : A
(ii) Total surface area (S) of cylinder in terms of r is
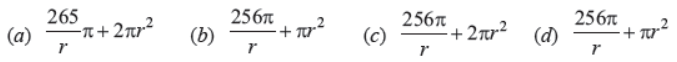
Answer : C
(iii) For maximum or minimum surface area, dS/dr = 0 which is equal to
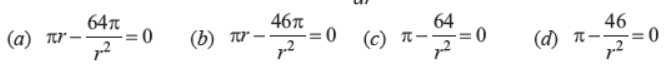
Answer : A
(iv) For minimum surface area of cylindrical can, value of r is
(a) 3 cm
(b) 1 cm
(c) 4 cm
(d) 2 cm
Answer : C
(v) Surface area of cylindrical can is minimum at h = ……………… cm
(a) 2
(b) 4
(c) 6
(d) 8
Answer : D
Q18. A class consists of 100 students. 25 of them are girls and 75 boys. 20 of them are rich and remaining poor, 40 of them are fair complexioned.

Based on the above information answer the following:
(i) Probability of selecting a fair complexioned student is
(a) 2/5
(b) 1/5
(c) 3/5
(d) 4/5
Answer : A
(ii) Probability of selecting a rich student is
(a) 2/5
(b) 1/5
(c) 3/5
(d) 4/5
Answer : C
(iii) Probability of selecting a girl
(a) 2/5
(b) 3/4
(c) 1/4
(d) 3/5
Answer : C
(iv) Find the probability of selecting a fair complexioned rich girl.
(a) 0.1
(b) 0.21
(c) 0.12
(d) 0.02
Answer : D
(v) Find the probability of selecting a fair complexioned rich boy.
(a) 0.06
(b) 0.14
(c) 0.16
(d) 0.02
Answer : A
Part–B
Section–III
All questions are compulsory. In case of internal choices attempt any one.
Q19. If tan–1 (a/x) + tan−1 (b/x) = π/2. find the value of x.
Answer : √ab
Q20. Using determinants, find the area of the triangle with vertices (– 3, 5), (3, – 6), (7, 2).
Answer : 46 sq. units.
OR
For what value of k, the points (1, 5) (k, 1) and (11, 7) are collinear?
Answer : k = – 19
Q21. Discuss the continuity at the point ‘a’ of the function
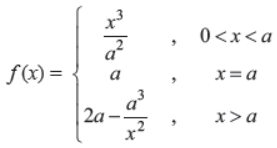
Answer : f (x) is continuous at x = a.
Q22. Determine the equation of the normal line to the curve y = 3√5–x at the point (– 3, 2).
Answer : 12x – y + 38 = 0
Q23. Evaluate:
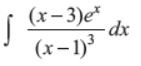
Answer :
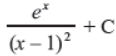
OR
Evaluate :
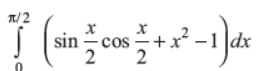
Answer :
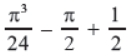
Q24. Find the area of the parabola y2 = 4ax bounded by its latus rectum.
Answer : 8/3 a2 sq. units
Q25. Solve the differential equation sin–1 (dy/dx) = x+y.
Answer : tan (x + y) – sec (x + y) = x + C
Q26. Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Answer : ……..?
Q27. Find the distance of the point (7, 2, 4) and the plane determined by the points A(2, 5, – 3), B(–2, –3, 5) and C(5, 3, –3)
Answer : √29
Q28. A problem in mathematics is given to 3 students whose chances of solving it are 1/2 ,1/3 , 1/4 What is the probability that the problem is solved?
Answer : 3/4
OR
The odds against solving a problem by A and B are 3 : 2 and 2 : 1. Find the probability of getting the problem solved.
Answer : 3/5
Section-IV
All questions are compulsory. In case of internal choices attempt any one.
Q29. Let W denote the words in the English Dictionary. Show that the relation R is defined as {(x, y) ∈ W × W: the words x and y have at least one letter in common} is reflexive, symmetric but not transitive.
Answer :
Q30. If
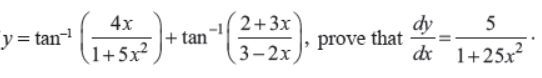
Answer : …..?
Q31. Prove that the greatest integer function defined by f (x) = [x], 0 < x < 3 is not differentiable at x = 1 and x = 2.
Answer : …..?
OR
If x = 2 cos t – cos 2t, y = 2 sin t – sin 2t, find d2y/dx2 at t = π/2.
Answer : –3/2
Q32. Find the interval in which the function f given by f (x) = x100 + sin x – 1 strictly increasing?
Answer : (π/2 ,π)
Q33. Evaluate: y cos x cos 2x cos 3x dx
Answer :
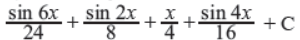
Q34. Find the area of the region bounded by the curves y2 = 4x, y-axis and the line y = 3.
Answer : 9/4 sq. units
OR
Find the area of the circle 4×2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Answer : √2+6 + 9/4 Sin–1 2√2/3.
Q35. Solve:
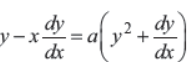
Answer : y = C(x + a) (1 – ay)
Section-V
All questions are compulsory. In case of internal choices attempt any one.
Q36. Show that
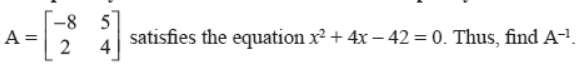
Answer :
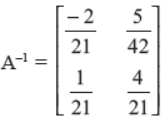
OR
Find the matrix X for which
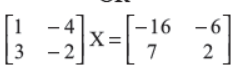
Answer :
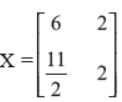
Q37. Show that the line whose vector equation r̅ = 2î – 2ĵ + 3k̂ + λ(î – ĵ + 4k̂) is parallel to the plane whose vector equation is r̅ = (î + 5ĵ + k̂) = 5. Also, find the distance between them.
Answer : 10√3/9
OR
Find the equation of the planes through the points (0, 4, – 3), (6, – 4, 3) other than the plane through the origin, which cut off, from the axes, intercepts whose sum is zero.
Answer : 6x + 3y – 2z = 18 and 2x – 3y – 6z = 6
Q38. Solve the following linear programming problem (L.P.P.) graphically.
Maximize Z = 22x + 18y.
Answer : Maximum value of Z = 392 and is attained at (8,12)
Subject to the constraints
x + y ≤ 20
360x + 240y ≤ 5760
and x ≥ 0, y ≥ 0
Answer : (a) p =q/2
OR
The corner points of the feasible region determined by the system of linear constraints are as shown below:
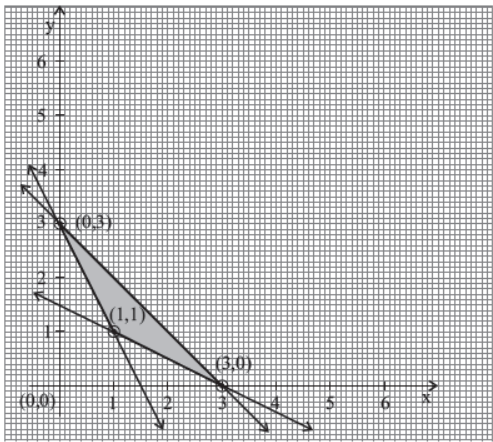
Answer the following:
(a) Let Z = px + qy, where p, q > 0. Find the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1)
Answer : (a) p =q/2
(b) Let Z = 4x + 6y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.
Answer : (b) Maximum value of Z is18 at (0, 3) and minimum value of Z is 10 at (1, 1).