Please refer to Class 12 Mathematics Sample Paper With Solutions Set H provided below. The Sample Papers for Class 12 Mathematics have been prepared based on the latest pattern issued by CBSE. Students should practice these guess papers for class 12 Mathematics to gain more practice and get better marks in examinations. The Sample Papers for Mathematics Standard 12 will help you to understand the type of questions which can be asked in upcoming examinations.
SECTION – A
1. If a̅ = 7î + ĵ- 4k̂ and b̅ = 2î + 6ĵ + 3k̂, then find the projection of a̅ on b̅ .
Solution:

2. Find λ, if the vectors a̅ = a̅ + 3ĵ + k̂, b̅ = 2î – ĵ – k̂and c̅ = λĵ + 3k̂are coplanar.
Solution: Since the given vectors are coplanar so, [a̅ b̅ c̅] = 0

3. If a line makes angles 90o , 60o and θ with x, y and z-axis respectively, where θ is acute angle, then find θ .
Solution: Here α = 90o , β = 60o and γ = θ Since cos2 α + cos2 β + cos2 γ =1
So, cos2 90o + cos2 60o + cos2 θ =1 ⇒ 0 + 1/4 + cos2 θ = 1 ⇒ cos2 θ = 3/4
⇒ cos θ = ±√3/2 ⇒ cos θ√3/2
⇒ cos θ = cos π/6 ∴ θ = π/6 [Since θ is an acute angle.
4. Write the element a23 of a 3 x 3 matrix A = (aij) whose elements aij are given by aij = |i-j|/2 .
Solution: We have aij = |i-j|/2 ∴ a23 = |2-3|/2 = 1/2 .
5. Find the differential equation representing the family of curves v = A/r + B , where A and B are arbitrary constants.
Solution: Given v = A/r + B ⇒ dv/dr = -A/r2 + 0
⇒ r2 , dv/dr = -A ⇒ r2 , d2v/dr2 + dv/dr (2r) = 0
∴ r,d2v/dr2 + 2 dv/dr = 0 is the required differential equation.
6. Find the integrating factor of the differential equation (e-2√x/√x – y/√x)dx/dy = 1 .
Solution: We have (e-2√x/√x – y/√x)dx/dy = 1 ⇒ dy/dx + y/√x = e-2√x/√x
On comparing to dy/dx + P(x)y = Q(x) , we observe P(x) = 1/√x and Q(x) = e-2√x/√x
∴ Integrating Factor = e∫1/√x dx = e2√x .
7. If A =
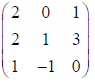
find A2 – 5A + 4I and hence find a matrix X such that A2 – 5A + 4I + X = O .
Solution:
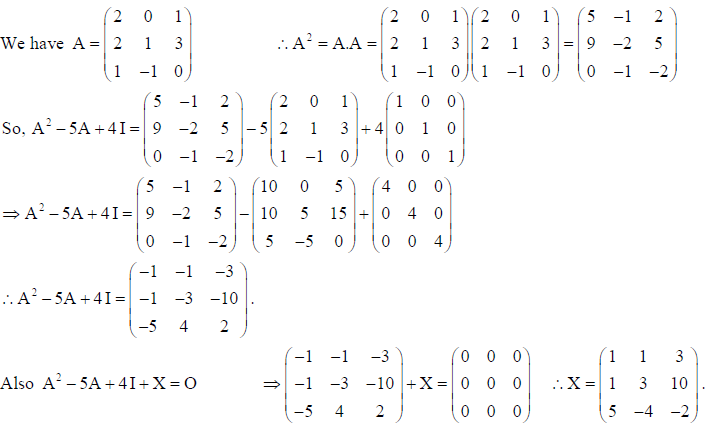
OR
If A =

find (A’)-1 .
Solution:

8. If f(x) =

using properties of determinants find the value of f (2x) – f (x) .
Solution:


⇒ f(x) = (a + x)(a2 + ax) – 0 + 0 ∴ f (x) = a(a + x)2
Now f (2x) – f (x) = a(a + 2x)2 – a(a + x)2
⇒ f (2x) – f (x) = a[a2 + 4x2 + 4ax – a2 – x2 – 2ax]
⇒ f (2x) – f (x) = a[3x2 + 2ax] ∴ f (2x) – f (x) + ax(3x + 2a) .
9. Find : ∫ dx/sin x + sin 2x
Solution:

OR
Integrate x2-3x+1/√1-x2 w.r.t. x.
Solution:

10. Evaluate :

Solution:
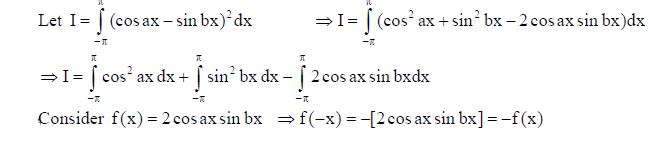
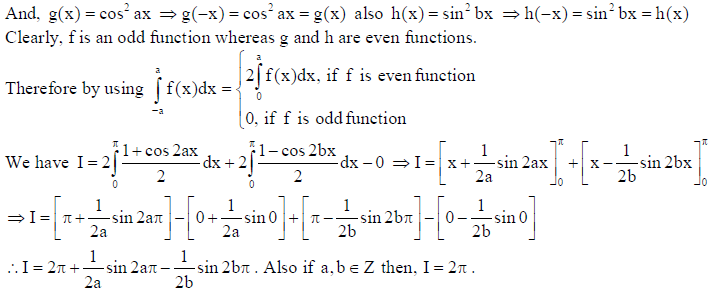
11. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Solution: Let E be the event that a red ball and another black ball is drawn.
Let E1 be the event that 1 or 2 appears on the die.
Let E2 be the event that 3, 4, 5 or 6 appears on the die.

OR
An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
Solution: Let X denote the number of heads so, it can take values 0, 1, 2, 3, 4.
Let E : head appears on the coin. ∴ P(E) = 1/2 , P(Ε̅) = 1/2 .
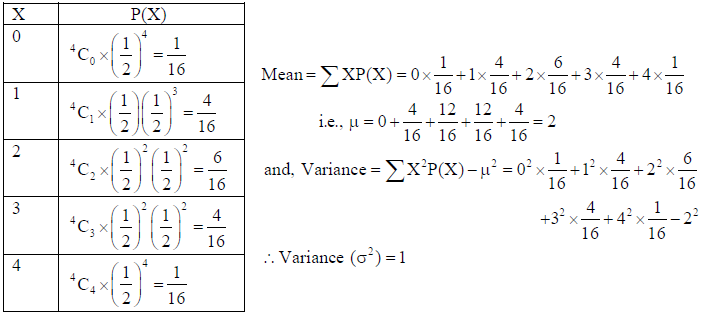
12. If r̅ = xî + yĵ + zk̂, find (r̅ x î) . (r̅ x ĵ) + xy .
Solution:


13. Find the distance between the point (–1, –5, –10) and the point of intersection of the line x-2/3 = y+1/4 = z-2/12 and the plane x – y + z = 5.
Solution: Let the line L : x-2/3 = y+1/4 = z-2/12 = λ and the plane π : x – y + z = 5 . Let P(–1, –5, –10).
∴ coordinates of random point on L : M(3λ + 2, 4λ – 1, 12λ + 2) .
If the line & plane intersect then M must lie on plane π
i.e., 3λ + 2 – 4λ + 1+12λ + 2 = 5 ⇒ λ = 0
∴ M(2,-1, 2) . Therefore, PM = √(2+1)2 + (-1 + 5)2 + (2+10)2 = 13 units .
14. If sin[cot-1(x +1)] = cos(tan-1 x) , then find x.
Solution:

OR
If (tan-1 x)2 + (cot-1 x2) = 5π2/8 , then find x.
Solution:

15. If y = tan-1(√1+x2 + √1-x2/√1+x2 – √1-x2 , x2 ≤ 1 , then find dy/dx .
Solution:


16. If x = a cosθ + bsin θ and, y = a sin θ – bcosθ , show that y2 , d2y/dx2 – x dy/dx + y = 0 .
Solution: Given x = a cosθ + bsin θ and, y = a sin θ – bcosθ
⇒ dx/dθ = -a sin θ + b cosθ and, dy/dθ = a cosθ + b sin θ
∴ dy/dx = dy/dθ x dθ/dx = a cosθ + b sin θ/b cosθ – a sin θ = -x/y …(i)
⇒ y , dy/dx = -x ⇒ y , d2y/dx2 + dy/dx x dy/dx = -1
By (i), we get : y , d2y/dx2 + (-x/y) x dy/dx + 1 = 0 ∴ y2 , d2y/dx2 – x dy/dx + y = 0 .
17. The side of an equilateral triangle is increasing at the rate of 2cm/s. At what rate is its area increasing when the side of the triangle is 20cm?
Solution: Let a denote the side length of the triangle so, da/dt = 2cms-1 .
Since area of the equilateral triangle is A = √3 a2/4 ⇒ dA/dt = √3 a/2 x da/dt

18. Find : ∫(x+3)√3 – 4x -x2 dx .
Solution: Let I = ∫(x+3)√3 – 4x -x2 dx
Consider x + 3 = A d/dx [3 – 4x – x2] + B ⇒ x + 3 = A[- 4 – 2X] + B
On equating the coefficients of like terms, we get : A = -1/2 , B = 1

19. Three schools A, B and C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of ₹ 25, ₹ 100 and ₹ 50 each. The number of articles sold are given below :

Find the funds collected by each school separately by selling the above articles. Also find the total funds collected for the purpose.
Write one value generated by the above situation.
Solution: Let the funds collected by schools A, B and C be x, y and z (in ₹) respectively.

By equality of matrices, we get : x = 7000, y = 6125, z = 7875 .
So the funds collected by school A is ₹ 7000, by school B is ₹ 6125 and by school C is ₹ 7875.
And, total funds collected = ₹ (7000 + 6125 + 7875) = ₹ 21000.
SECTION – C
20. Let N denote the set of all natural numbers and R be the relation on N×N defined by (a,b)R(c,d) if ad(b + c) = bc(a + d) . Show that R is an equivalence relation.
Solution: We have (a,b)R(c,d) given as ad(b + c) = bc(a + d)
Reflexivity : Let (a, b)∈ N x N
⇒ ab(b + a) = ba(a + b) ∴ (a,b)R(a,b)
So, R is reflexive.
Symmetry : Let (a, b), (c,d)∈ NxN
Let (a, b)R(c,d) ⇔ ad(b + c) = bc(a + d)
⇒ cb(d + a) = da(c + b) ∴ (c,d)R(a,b) .
So, R is symmetric.
Transitivity : Let (a, b), (c,d), (e,f )∈ NxN
Since (a, b)R(c,d) ⇔ ad(b + c) = bc (a+b) ⇒ 1/b + 1/c = 1/a + 1/d [Dividing by abcd both sides
Now (a, b)R(c,d) ⇔ 1/a + 1/d = 1/b + 1/c and (c,d)R(e, f ) ⇔ 1/c + 1/f = 1/d + 1/e
Adding these two equations, 1/a + 1/d + 1/c + 1/f = 1/b + 1/c + 1/d + 1/e ⇒ 1/a + 1/f = 1/b + 1/e ⇒ (a, b)R(e,f )
Hence R is transitive.
Since R is reflexive, symmetric and transitive so, it is an equivalence relation.
21. Using integrals, find the area of the triangle formed by positive x-axis, and the tangent and the normal to the circle x2 + y2 = 4 at (1, 3 ) .
Solution:

OR
Evaluate

Solution:
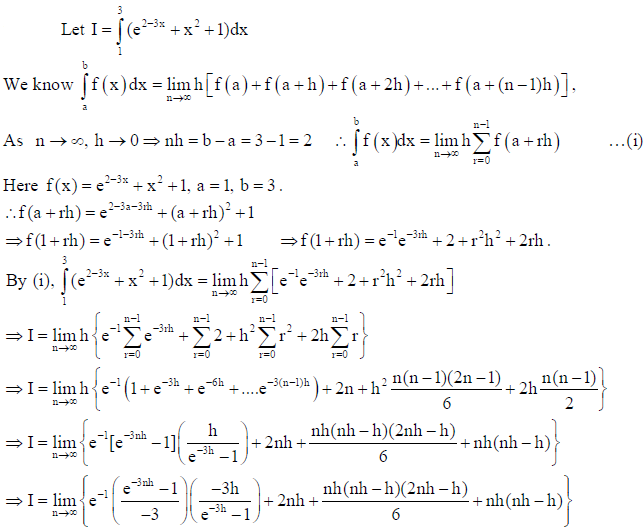

22. Solve the differential equation : (tan-1 y – x) dy = (1+y2) dx .
Solution: We have (tan-1 y – x) dy = (1+y2) dx ⇒ dx/dy + x/1+y2 = tan-1 y/1+y2
It’s linear differential equation of the form dx/dy + P(y) x = Q(y) where
P(y) = 1/1+y2 , Q(y) = tan-1 y/1+y2

OR
Find the particular solution of the differential equation dy/dx = xy/x2+y2 given that y = 1 when x = 0 .
Solution:

23. If lines x-1/2 = y+1/3 = z-1/4 and x-3/1 = y-k/2 = z/1 intersect, find the value of k and hence find the equation of the plane containing these lines.
Solution: Let L1 : x-1/2 = y+1/3 = z-1/4 = λ and, L2 : x-3/1 = y-k/2 = z/1 = μ
The coordinates of random points on these lines are :
P(2μ + 1,3μ -1, 4μ +1) and Q(μ + 3, 2μ + k,μ)
Since 1 2 L and L intersect each other so, the points P and Q must coincide for some real values
of λ and μ . That is 2λ +1 = μ + 3…(i),3λ -1 = 2μ + k…(ii), 4λ + 1 = μ…(iii)
Solving (i) and (iii), we get : λ = -3/2 , μ = -5

24. If A and B are two independent events such that P(A̅∩B) = 2/15 and P(A∩B̅) = 1/6 , then find P(A) and P(B) .
Solution: Since A and B are two independent events so A̅ and B , A and B̅ are independent events.
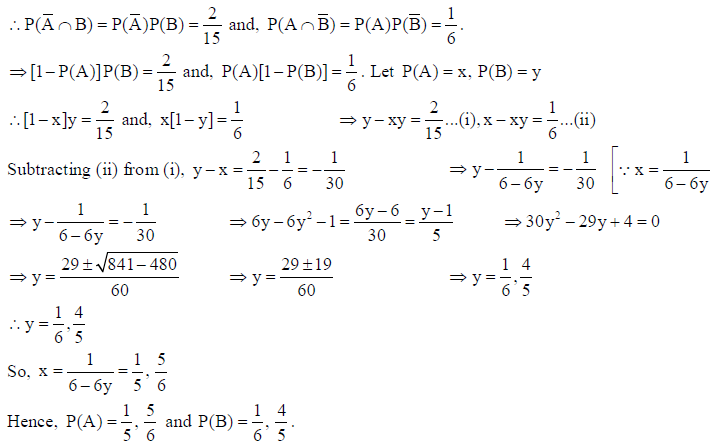
25. Find the points of local maxima and local minima, of the function f (x) = sin x – cos x, 0 < x < 2π. Also find the local maximum and local minimum values.
Solution: We have f (x) = sin x – cos x, 0 < x < 2π ⇒ f ‘(x) = cos x + sin x , f ”(x) = -sin x + cos x
For local points of maxima and minima f ‘(x) = cos x + sin x = 0

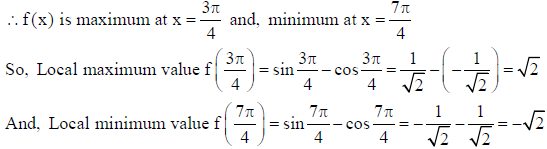
26. Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 8, 3x + y ≤ 6, x + y ≤ 4, x ≥ 0, y ≥ 0 .
Solution: To maximize : z = 2x + 5y
Subject to constraints : 2x + 4y ≤ 8, 3x + y ≤ 6, x + y ≤ 4, x ≥ 0, y ≥ 0 .


So, maximum value of z is 10.


