Please refer to Introduction To Euclids Geometry Class 9 Mathematics Notes And Questions Class 9 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 9. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 9 Mathematics Introduction To Euclids Geometry Notes and Questions
Definitions in Euclidian Geometry
Geometry Around Us
Our daily life is filled with geometry—the pure mathematics of points, lines, curves and surfaces. We can observe various shapes and angles in the objects that surround us.
Observe, for example, this table and its rectangular surface; the boomerang and its angular shape; the bangle and its circular shape.

Euclid, an ancient Greek mathematician, observed the various types of objects around him and tried to define the most basic components of those objects. He proposed twenty-three definitions based on his studies of space and the objects visible in daily life. Let us go through this lesson to learn each of Euclid’s definitions.
Know Your Scientist


Did You Know?
The Elements is a great collection of basic geometrical concepts and ideas. The content in it is based on the works of a few great mathematicians, including Pythagoras, Thales, Plato, Aristotle, Eudoxus and Menaechmus. This work had been the most commonly used and the premier source of geometrical concepts for over 2000 years since its publication. It is believed to be the most translated, published and studied book after the Bible in the western world.
Definitions Given by Euclid
Euclid gave the definitions of a few very basic attributes of objects that are normally around us. These definitionsare listed below.
1. A point is that which has no part.
2. A line is a breadth-less length.
3. The extremities of a line are called points.
4. A straight line is one that lies evenly with the points on itself.
5. A surface is that which has length and breadth only.
6. The edges of a surface are lines.
7. A plane surface is one that lies evenly with the straight lines on itself.
8. A plane angle is the inclination to each other of two lines in a plane, which meet each other and do not lie in a straight line.
9. When the lines containing the angle are straight, the angle is called rectilinear.
10. When a straight line set up on another straight line makes the adjacent angles equal to each other, each of the equal angles is right and the straight line standing on the other is called a perpendicular to that on which it stands.
11. An obtuse angle is an angle greater than the right angle.
12. An acute angle is an angle less than the right angle.
13. A boundary points out the limit or extent of something.
14. A figure is that which is contained by any boundary or boundaries.
Definitions Given by Euclid
15. A circle is a plane figure consisting of a set of points equidistant from a reference point.
16. This reference point is called the centre of the circle.
17. The diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects
the circle.
18. A semicircle is the figure contained by the diameter and the circumference cut off by it.
Also, the centre of the semicircle is the same as that of the circle.
19. Rectilinear figures are those that are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
20. Of trilateral figures, an equilateral triangle is that which has its three sides equal; an isosceles triangle is that which has only two of its sides equal; and a scalene triangle is that which has its three sides unequal.
21. Of trilateral figures, a right-angled triangle is that which has a right angle; an obtuseangled triangle is that which has an obtuse angle; and an acute-angled triangle is that which has its three angles acute.
22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong is that which is right-angled but not equilateral; a rhombus is that which is equilateral but not right-angled; and a rhomboid is that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let any other type of quadrilateral be called a trapezium.
23.Parallel lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
Did You Know?
Although Euclid defines ‘point’, ‘line’ and ‘plane’, these geometric quantities are now considered by mathematicians as undefined. This is because these three quantities are considered the basic entities in geometry. These three entities are used for defining other geometric shapes and concepts.
Solved Examples
Easy
Example 1: Which of the following pairs of terms are considered ‘undefined’ in geometry?
A. Point and circle
B. Point and line
C. Circle and line
D. Circle and radius
Solution:
The correct answer is B.
Point, line and plane are considered ‘undefined’ in geometry.
Example 2: Fill in the blanks.
i) The extremities of a plane surface are known as __________.
ii) An __________ angle is greater than the right angle.
iii) The __________ of a circle is the straight line passing through the centre of the circle.
iv) A trilateral figure is contained by__________ lines.
v) The __________ is a trilateral figure whose all sides are equal.
Solution:
i) lines
ii) obtuse
iii) diameter
iv) three
v) equilateral triangle
Axioms in Euclidian Geometry
Euclid’s Axioms
Euclid assumed certain properties to be universal truths that did not need to be proved. He classified these properties as axioms and postulates. The properties that were not specific to geometry were referred to as common notions or axioms.
He compiled all the known mathematical works of his time into the Elements. Each book of the Elements contains a series of propositions or theorems, varying in number from about ten to hundred. These propositions or theorems are preceded by definitions. In Book I, twenty-three definitions are followed by five postulates. Five common notions or axioms are listed after the postulates.
In this lesson, we will study some of Euclid’s axioms.
Statements of Euclid’s Axioms
Here are a few of Euclid’s axioms.
I. Things that are equal to the same thing are also equal to one another.
II. If equals are added to equals, then the wholes are equal.
III. If equals are subtracted from equals, then the remainders are equal.
IV. Things that coincide with one another are equal to one another.
V. The whole is greater than the part.
VI. Things that are double of the same things are equal to one another.
VII. Things that are halves of the same things are equal to one another.
These axioms have a lot of practical applications in different branches of science.
Axioms I and II
Let us start with the first axiom which states that things that are equal to the same thing are also equal to one another.
Let us suppose the area of a rectangle is equal to the area of a triangle and the area of that triangle is equal to the area of a square. Then, according to the first axiom, the area of the rectangle is equal to the area of the square. Similarly, if a = b and b = c, then we can say that a = c.
Now, the second axiom states that if equals are added to equals, then the wholes are equal.
Let us take a line segment AD in which AB = CD.

Let us add BC to both sides of the above relation (‘equals are added’). Then, according to the second axiom, we can say that AB + BC = CD + BC, i.e., AC = BD.
Concept Builder
• A line segment is a part of a line that has two end points. It has a definite length.
• A line segment corresponds to the shortest distance between two points, say P and Q. The line segment joining the points P and Q is denoted as —PQ .

Solved Examples
Easy
Example 1: Show that a line segment has only one midpoint.
Solution:
Let us suppose that a line segment PQ has two midpoints R and S.

Case 1: When R is the midpoint, we have PR = RQ.
One of Euclid’s axioms states that if equals are added to equals, then the wholes are equal.
So, on adding PR to both sides of the above relation, we obtain:
2PR = PR + RQ
⇒ PQ = 2PR … (1)
Case 2: When S is the midpoint, we have PS = SQ.
Again, we will use the previously stated axiom and add PS to both sides of the above relation.
2PS = PS + SQ
⇒ PQ = 2PS … (2)
On comparing equations 1 and 2, we obtain:
2PS = 2PR
PS = PR (Things that are halves of the same things are equal to one another)
This implies that points S and R lie at the same place on line PQ, which is clearly not the case. Thus, our assumption is wrong. Hence, we can conclude that a line segment can have only one midpoint.
Axiom III
The third axiom states that if equals are subtracted from equals, then the remainders are equal.
Let us consider the following rectangles ABCD and PQRS.
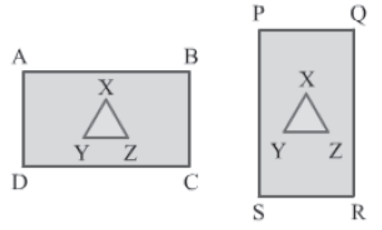
Suppose the areas of the rectangles are equal. Now, let us remove a triangle XYZ (as shown in the figure) from each rectangle. Then, according to the third axiom, we can say that the area of the remaining portion of rectangle ABCD is equal to the area of the remaining portion of rectangle PQRS.
Solved Examples
Easy
Example 1: In the given line segment AD, AC = BD. Prove that AB = CD.

Solution:
It is given that AC = BD in line segment AD.
One of Euclid’s axioms states that if equals are subtracted from equals, then the remainders are equal.
So, on subtracting BC from both sides of the above relation, we obtain:
AC − BC = BD − BC
⇒ AB = CD
Axioms IV and V
The fourth axiom states that things that coincide with one another are equal to one another.
This axiom is sometimes used in geometrical proofs.
Let us consider a point Q lying between points P and R of a line segment PR, as is shown in the figure.

We can see that (PQ + QR) coincides with the line segment PR. So, as per the fourth axiom, we can say that PQ + QR = PR.
Now, the fifth axiom states that the whole is greater than the part.
Let us again consider the line segment PR shown above. We can see that PQ is a part of PR.
So, as per the fifth axiom, we can say that PR (i.e., the whole) is greater than PQ (i.e., the part). Mathematically, we write it as PR > PQ.
Axioms VI and VII
The sixth and seventh axioms are interrelated. The former states that things that are double of the same things are equal to one another, whilethe latter states thatthings that are halves of the same things are equal to one another.
Let us consider two identical circles with radii
r1 and r2. Also, suppose their diameters are d1 and d2 respectively.
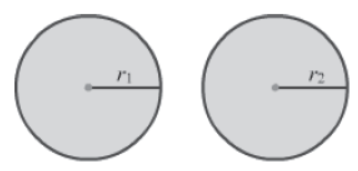
As the circles are identical, their radii are equal.
∴ r1 = r2
Now, as per the sixth axiom, we can say that 2r1 = 2r2
∴ d1 = d2
Hence, we can say that if two circles have equal radii, then their diameters are also equal.
Now, instead of taking the radii as equal, let us say that the diameters of the two circles are equal. Then, as per the seventh axiom, we can say that the radii of the two circles are also equal.
Euclid’s First Four Postulates
Meaning of Postulates
Certain things are considered universal truths that need not be proved. Consider, for example, the following: the sun rises from the east; Sunday comes after Saturday; March has 31 days. These things are universally true; hence, they do not need to be proven.
Similarly, certain geometrical properties are regarded as universal truths. Euclid identified and presented such properties in the Elements. The properties specific to geometry were classified by him as postulates. In Book I, twenty-three definitions are followed by five postulates. Let us learn these postulates in this lesson.
Did You Know?
• The Elements includes the number theory that explains the relation between perfect numbers and Mersenne primes, where Mersenne primes are positive integers that are 1 less than any power of 2 or can be written in the form 2P-1 .
• In the Elements, Euclid explains how there are infinitely many prime numbers.
Additionally, the book includes Euclid’s lemma on factorization as well as Euclidean algorithm for finding the greatest common factor of two numbers.
Postulates I and II
Postulate I: It is possible to draw a straight line from any point to any other point.
As per this postulate, if we have two points P and Q on a plane, then we can draw at least one line that simultaneously passes through the two points. Euclid does not mention that only one line can pass through two points, but he assumes the same. The fact that only one line can pass through any two points is illustrated in the following figure.

Postulate II: A terminated line can be produced indefinitely.
This postulate can be considered an extension of the first postulate. According to this postulate, we can make a straight line that is different from a given line by extending its points on both sides of the plane.
In the following figure, MN is the original line, while M’N’ is the new line formed by extending the original line in either direction.

Know More
Infinitely many straight lines can pass through a given point.
Consider the following figure.
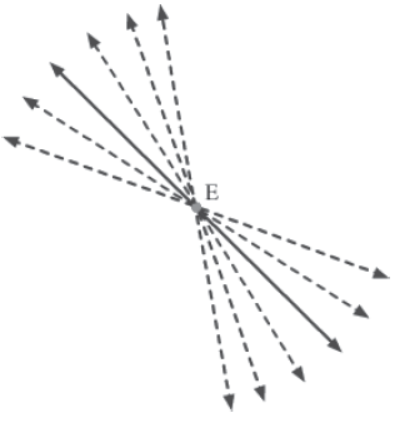
In the figure, many lines can be seen passing through point E. In fact, infinitely many lines can pass through E.
Postulates III and IV
Postulate III: It is possible to describe a circle with any centre and radius.
According to Euclid, a circle is a plane figure consisting of a set of points that are equidistant from a reference point. It can be drawn with the knowledge of its centre and radius.
Circles with different radii have different sizes but the same shape.
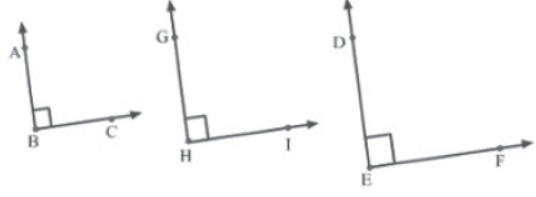
Postulate IV: All right angles are equal to one another.
A right angle is unique in the sense that it measures exactly 90°. Hence, all right angles are of the measure 90°, irrespective of the lengths of their arms. Thus, all right angles are equal to one another. For example, in the following figure, ∠ABC = ∠GHI = ∠DEF = 90°.
Did You Know?
Unlike right angles, acute and obtuse angles are not unique in the sense that their measures lie in the ranges 0°−89° and 91°−179° respectively. Hence, the measure of one acute angle is not the same as the measure of another acute angle. Similarly, each obtuse angle has a different measure.
Know Your Scientist
Thales

Thales also generalized the concept of equality of the base angles of an isosceles triangle.
He also propounded a few general notions such as ‘all straight angles are equal’, ‘equals subtracted from equals are equal’ and ‘equals added to equals are equal’. These theorems have helped in the evolution of modern mathematics.
Following rules were observed while measuring the lengths of line segments and angles.
These rules were not stated separately but these were assumed by Euclid in the derivation of new postulates. These can be taken as additional postulates.
Rule 1. Every line segment has a positive length.
Rule 2. If a point R lies on the line segment PQ, then the length of PQ is equal to the sum of the lengths of PR and RQ. That is, PQ = PR + RQ
Rule 3. Every angle has a certain magnitude. A straight angle measures 180°.
Rule 4. If rays —OP , —OQ and —OR are such that OR lies between OP and OQ , then ∠POQ = ∠POR + ∠ROQ
Rule 5. If the angle between two rays is zero then they coincide. Conversely, if two rays coincide, then angle between them is either zero or an integral multiple of 360°.
Solved Examples
Medium
Example 1: Prove that an isosceles triangle can be constructed on any given line segment.
Solution:
Say we have a line segment AB of any length.
Let us extend AB to the points X and Y in either direction, such that AX = BY.
Now, as per Euclid’s second axiom, we have:
AX + AB = BY + AB
⇒ BX = AY … (1)
Using Euclid’s third postulate, let us draw a circle with A as the centre and AY as the radius.
Similarly, let us draw another circle with B as the centre and BX as the radius. Let the circles intersect at a point C.
Now, let us join A and B to C to get the line segments AC and BC respectively. We thus obtain ΔACB.
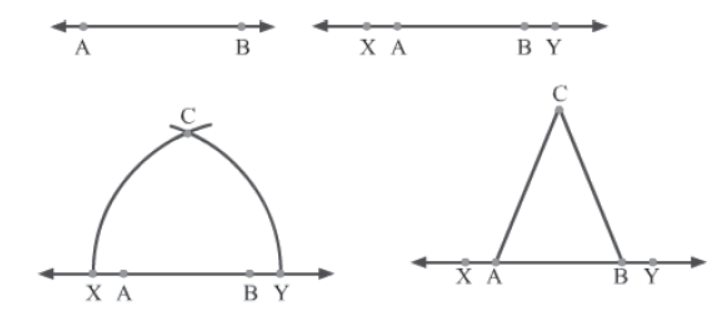
Now, we have to prove that ΔACB is isosceles, i.e., AC = BC.
AY and AC are the radii of the circle with centre A; BX and BY are the radii of the circle with
centre B.
∴ AY = AC … (2)
Similarly, BX = BC … (3)
From equations 1, 2 and 3 and Euclid’s axiom that things which are equal to the same thing are equal to one another, we can conclude that AC = BC.
So, ΔACB is isosceles.
Euclid’s Fifth Postulate
Euclid’s Fifth Postulate
Do you know what is meant by a transversal? When two lines are intersected by a common line, the common line is known as a transversal. Examples of transversals can be found in the various things that surround us. Look, for example, at the house shown in the figure.
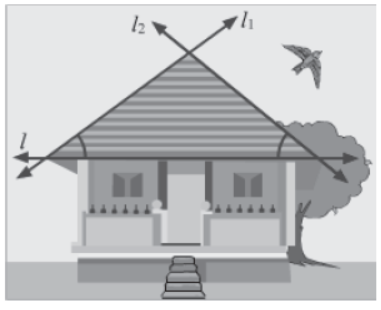
Three edges of the roof have been labelled as l, l1 and l2. Notice how line l intersects lines l1 and l2. Hence, line l is a transversal. Similarly, lines l and l1 are intersected by the transversal l2 and lines l and l2 are intersected by the transversal l1.
Euclid’s fifth postulate (also known as the parallel postulate) is all about transversals.
This postulate lays down the conditions for the intersection of the lines cut by a transversal. We will study about this postulate in this lesson.
Did You Know?
The geometrical system described in the Elements was for long known simply as ‘geometry’. It was considered to be the only geometry possible. Today, however, that system is often referred to as ‘Euclidean geometry’ to distinguish it from other ‘non- Euclidean geometries’ that mathematicians discovered in the nineteenth century.
Concept Builder
A transversal is a line that intersects two or more lines at distinct points. When the lines are parallel, the transversal produces several congruent and supplementary angles.
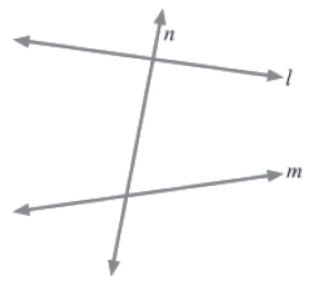
In the above figure, line n intersects the two lines l and m; therefore, n is a transversal.
Euclid’s Fifth Postulate
Statement: If a straight line falling on two straight lines forms interior angles that together measure less than two right angles
on the same side of it, then the two straight lines, when produced indefinitely, meet on that side on which the sum of the angles is less than two right angles.
Explanation:
Let l be a transversal intersecting two lines l1 and l2. Say ∠A and ∠B are the interior angles formed on the same side by the transversal. Now, if the sum of ∠A and ∠B is less than two right angles (i.e., ∠A + ∠B < 180°), then l1 and l2 will intersect (when extended indefinitely) on the same side as ∠A and ∠B. This is shown in the following figure.
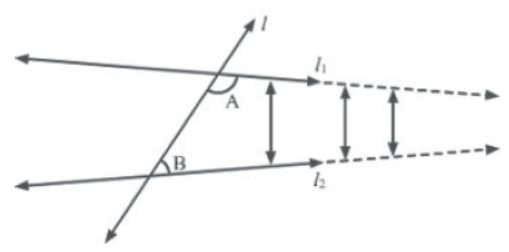
If we extend l1 and l2 on the same side as ∠A and ∠B, then we will find that the distance between the lines goes on decreasing. This indicates that the lines will intersect after some finite distance.
It is important to note that two other cases arise for the same situation involving transversal l and lines l1 and l2, i.e., the case when ∠A + ∠B > 180° and the case when ∠A + ∠B = 180°.
Did You Know?
In the Elements, Euclid does not use the fifth postulate until the twenty-ninth proposition.
He uses only the first four postulates for propositions 1−28.
Did You Know?
• A Hungarian mathematician named Janos Bolyai and a Russian mathematician named Nikolai Lobachevsky independently realized that completely self-consistent ‘non-Euclidean
geometries’ can be created without the parallel postulate.
• Mathematicians around the world have tried proving Euclid’s fifth postulate by using the other four. They have provided different versions of this postulate, which indirectly show the existence of parallel lines.
Know Your Scientist

He is credited for an axiom about parallel lines that is considered an alternative to Euclid’s parallel postulate. This axiom is known as Playfair’s axiom and it states that:
For every line in a plane, there exists another unique line in the same plane parallel to the given line, which passes through a point placed at a certain distance from that line.
This can be understood from the following figure.
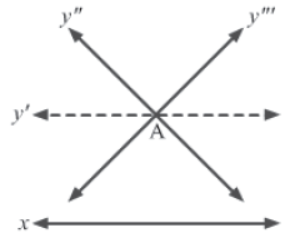
It is clear from the figure that out of the various lines passing through point A, only line y′ is parallel to line x.
Solved Examples
Easy
Example 1: In the given figure, if l||m and n is the transversal, then find the value of x.
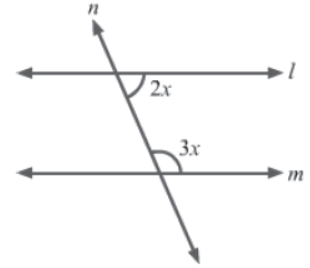
Solution:
It is given that l||m and n is the transversal.
According to Euclid’s fifth postulate, if the sum of the interior angles made by the transversal on the two lines is equal to two right angles, i.e., 180°, then the lines are parallel.
∴ 2x + 3x = 180° (&because l||m)
⇒ 5x = 180°
⇒ ∴ x = 180°/5 = 36°
Medium
Example 1: In the given figure, prove that AB||CD and CD > AB.
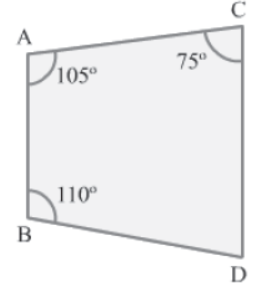
Solution:
Consider the transversal AC intersecting the line segments AB and CD. Here, ∠CAB and ∠ACD are the interior angles made by AC.
From the figure, we have:
∠CAB + ∠ACD = 105° + 75° = 180°
Hence, by Euclid’s fifth postulate, line segments AB and CD are parallel or AB||CD.
Now, consider the transversal AB intersecting the line segments AC and BD. Here, ∠CAB
and ∠ABD are the interior angles made by AB.
From the figure, we have:
∠CAB + ∠ABD = 105° + 110° = 215° > 180°
Thus, according to Euclid’s fifth postulate, if we extend AC and BD toward the right side (i.e., the same side where the sum of the interior angles is greater than two right angles),
then the distance between AC and BD will keep increasing.
Since AB||CD and CD meets AC and BD toward the right side of AB (i.e., where the distance between AC and BD keeps increasing when extended), we obtain that CD > AB.
Example 2: In the given figure, if x||y, then show that ABCD is a parallelogram.
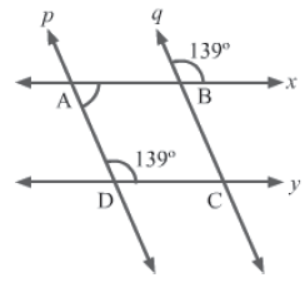
Solution:
Since x||y and p is the transversal, we have:
∠BAD + ∠ADC = 180° (By Euclid’s fifth postulate)
⇒ ∠BAD = 180° − ∠ADC
⇒ ∠BAD = 180° − 139°
⇒ ∠BAD = 41°
Also, ∠ABC = 139° (Vertically opposite angles at B made by x and q)
We have the lines p and q intersected by the transversal x. ∠BAD and ∠ABC are interior
angles made on the same side by x.
∠BAD + ∠ABC = 41° + 139° = 180°
∴ p||q (By Euclid’s fifth postulate)
Now, in ABCD, we have:
AB||CD (&because x||y)
AD||BC (&because p||q)
Hence, ABCD is a parallelogram.
