Please refer to Kinetic Theory Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Kinetic Theory Notes and Questions
Assumptions of Kinetic Theory of Gases
1. Every gas consists of extremely small particles known as molecules. The molecules of a given gas are all identical but are different from those of another gas.
2. The molecules of a gas are identical spherical, rigid and perfectly elastic point masses.
3. Their molecular size is negligible in comparison to intermolecular distance (10-9 m).
4. The speed of gas molecules lies between zero and infinity (very high speed).
5. The distance covered by the molecules between two successive collisions is known as free path and mean of all free path is known as mean free path.
6. The number of collision per unit volume in a gas remains constant.
7. No attractive or repulsive force acts between gas molecules.
8. Gravitational to extremely attraction among the molecules is ineffective due small masses and very high speed of molecules.
Gas laws
Assuming permanent gases to be ideal, through experiments, it was established that gases irrespective of their nature obey the following laws.
Boyle’s Law
At constant temperature the volume (V) of given mass of a gas is inversely proportional to its
pressure (p), i.e.,
V ∝ 1/p ⇒ pV = constant
For a given geas, p1V1 = p2V2
Charles’ Law
At constant pressure the volume (V) of a given mass of gas is directly proportional to its absolute temperature (T), i.e.,
V ∝ T ⇒ V / T = constant
For a given gas, V1/T1 = V2/T2
At constant pressure the volume (V) of a given mass of a gas increases or decreases by 1/273.15 of its volume at 0°C for each 1°C rise or fall in temperature.
Volume of the gas at t°Ce
Vt = V0 (1 + t/273.15)
where V0 is the volume of gas at 0°C.
Gay Lussacs’ or Regnault’s Law
At constant volume the pressure p of a given mass of gas is directly proportional to its absolute temperature T, i.e. ,
p ∝ T ⇒ V/T = constant
For a given gas,
p1/T1 = p2/T2
At constant volume (V) the pressure p of a given mass of a gas increases or decreases by
1/273.15 of its pressure at 0°C for each l°C rise or fall in temperature.
Volume of the gas at t°C, pt = p0 (1 + t/273.15)
where P0 is the pressure of gas at 0°C.
Avogadro’s Law
Avogadro stated that equal volume of all the gases under similar conditions of temperature and pressure contain equal number molecules. This statement is called Avogadro’s hypothesis.
According Avogadro’s law
(i) Avogadro’s number The number of molecules present in 1g mole of a gas is defined as Avogadro’s number.
NA = 6.023 X 1023 per gram mole
(ii) At STP or NTP (T = 273 K and p = 1 atm 22.4 L of each gas has 6.023 x 1023 molecules.
(iii) One mole of any gas at STP occupies 22.4 L of volume.
Standard or Perfect Gas Equation
Gases which obey all gas laws in all conditions of pressure and temperature are called perfect gases.
Equation of perfect gas pV=nRT
where p = pressure, V = volume, T = absolute temperature, R = universal gas constant and n = number of moles of a gas.
Universal gas constant R = 8.31 J mol-1K-1.
Real Gases
- Real gases deviate slightly from ideal gas laws because
- Real gas molecules attract one another.
- Real gas molecules occupy a finite volume.
Real or Van der Waal’s Gas Equation
(p + a/V2) (V – b) = RT
where a and b are called van der Waals’ constants.
Pressure due to an ideal gas is given by
p = (1/3).(mn/V). c2 = 1/3 ρ c2
For one mole of an ideal gas
P = (1/3).(M/V).c2
where, m = mass of one molecule, n = number of molecules, V = volume of gas, c = (c12 +c22 + … + cn2) / n allde root mean square (rrns) velocity of the gas molecules and M =
molecular weight of the gas. If p is the pressure of the gas and E is the kinetic energy per unit
volume is E, then
p = (2/3).E
Kinetic Energy of a Gas
(i) Average kinetic energy of translation per molecule of a gas is given by
E = (3/2) kt
where k = Boltzmann’s constant.
(ii) Average kinetic energy of translation per mole of a gas is given by
E = (3/2) Rt
where R = universal gas constant.
(iii) For a given gas kinetic energy
E ∝ T ⇒ E1/E2 = T1/T2
(iv) Root mean square (rms) velocity of the gas molecules is given by
(v) For a given gas c ∝ √T
(vi) For different gases c ∝1/√M
(vii) Boltzmann’s constant k = R/N
where R is ideal gas constant and N = Avogadro number.
Value of Boltzmann’s constant is 1.38 x 10-28 J/K.
(viii) The average speed of molecules of a gas is given by
(ix) The most probable speed of molecules of a gas is given by

Degree of Freedom
The degree of freedom for a dynamic system is the number of directions in which it can move freely or the number of coordinates required to describe completely the position and configuration of the system.
It is denoted by for N.
Degree of freedom of a system is given by
f or N = 3A – R
where A = number of particles in the system and R = number of independent relations.
Degree of Freedom
1. For monoatomic gas = 3
2. For diatomic gas = 5
3. For non-linear triatomic gas = 6
4. For linear triatomic gas = 7
Specific heat of a gas
(a) At constant volume, CV = f/2 R
(b) At constant pressure, cp = (f/2 + 1)R
(c) Ratio of specific heats of a gas at constant pressure and at constant volume is given by γ = 1 + 2/f
Mean Free Path
The average distance travelled by a molecule between two successive collisions is called mean free path (γ).
Mean free path is given by
γ = kT / √2 π σ2p
where σ = diameter of the molecule, p = pressure of the gas,
T = temperature and k = Botlzmann’s constant.
Mean free path
λ ∝ T and λ ∝ 1/p
Brownian Motion
The continuous random motion of the particles of microscopic size suspended in air or any liquid, is called Brownian of microscopic motion.
Brownian suspended motion in both is observed with many liquids and gases.
Brownian motion is due to the unequal bombardment of the suspended Particles by the molecules of the surrounding medium.
rest and Motion are relative terms, nobody can exist in a state of absolute rest or of absolute motion.
One dimensional motion:- The motion of an object is said to be one dimensional motion if only one out of three coordinates specifying the position of the object change with time. In such a motion an object move along a straight line path.
Two dimensional motion:- The motion of an object is said to be two dimensional motion if two out of three coordinates specifying the position of the object change with time. In such motion the object moves in a plane.
Three dimensional motion:- The motion is said to be three dimensional motion if all the three coordinates specifying the position of an object change with respect to time ,in such a motion an object moves in space.
The magnitude of displacement is less than or equal to the actual distance travelled by the object in the given time interval.
Displacement ≤ Actual distance
Speed:- It is rate of change of distance covered by the body with respect to time.
Speed = Distance travelled /time taken Speed is a scalar quantity .Its unit is meter /sec. and dimensional formula is [M0L1T-1] .It is positive or zero but never negative.
Uniform Speed:- If an object covers equal distances in equal intervals of time than the speed of the moving object is called uniform speed. In this type of motion, position – time graph is always a straight line.
Instantaneous speed:-The speed of an object at any particular instant of time is called instantaneous speed. In this measurement, the time Δt→0.
When a body is moving with uniform speed its instantaneous speed = Average speed = uniform speed.
Velocity:- The rate of change of position of an object in a particular direction with respect to time is called velocity. It is equal to the displacement covered by an object per unit time.
Velocity =Displacement /Time
Velocity is a vector quantity, its SI unit is meter per sec. Its dimensional formula is [M0L1T-1]. It may be negative, positive or zero.
When a body moves in a straight line then the average speed and average velocity are equal.
Acceleration:- The rate of change of velocity of an object with respect to time is called its acceleration.
Acceleration = Change in velocity /time taken
It is a vector quantity, Its SI unit is meter/ sec.2 and dimension is [M0L1T-2], It may be positive ,negative or zero.
Positive Acceleration:- If the velocity of an object increases with time, its acceleration is positive .
Negative Acceleration :-If the velocity of an object decreases with time, its
acceleration is negative . The negative acceleration is also called retardation or deacceleration.
Formulas of uniformly accelerated motion along straight line:-
For accelerated motion, For deceleration motion
V = u + at v = u – at
S = ut + 1/2 at2 S = ut – 1/2 at2
V2 =u2+ 2as V2= u2– 2as
Sn = u + a/2(2n- 1) Sn = u – a/2( 2n- 1)
Free fall :- In the absence of the air resistance all bodies fall with the same acceleration towards earth from a small height. This is called free fall. The acceleration with which a body falls is called gravitational acceleration (g).Its value is 9.8 m/sec2.
Relative Motion:- The rate of change of distance of one object with respect to the other is called relative velocity. The relative velocity of an object B with respect to the object A when both are in motion is the rate of change of position of object B with respect to the object A.
Relative velocity of object A with respect to object B
V→ AB =→ VA –→ B
When both objects are move in same direction, then the relative velocity of object B with respect to the object A
V→ BA =→ VB -+V A
When the object B moves in opposite direction of object A .
V→ BA =V→ B +→V A
When VA and VB are incident to each other at angle Θ
VAB = (V2A + V2B – 2VAVBCos Θ)1/2
Scalars :- The quantities which have magnitude only but no direction. For example :
mass, length, time, speed , temperature etc.
Vectors :- The quantities which have magnitude as well as direction and obeys vector laws of addition, multiplication etc.
For examples : Displacement, velocity, acceleration, force , momentum etc.
Addition of Vectors :-
(i) Only vectors of same nature can be added.
(ii) The addition of two vector A and B is resultant R
⃗R = + ⃗A + B
And R = ( A2 + B2+ 2AB CosΘ)1/2
And tan β = B SinΘ/ ( A + B CosΘ) ,
Where Θ is the angle between vector A and vector B, And β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative →A+→ B =→B +→A
(iv) Vector addition is associative, (→A +→B ) +→C =→A + (→B +→C )
(v) R is maximum if Θ = 0 and minimum if Θ = 180 0.
Subtraction of two vectors :-
(i) Only vector of same nature can be subtracted.
(ii) Subtraction of B from A = vector addition of A and (-B),
⃗R = ⃗A –→B =→A + (→-B)
Where R = [ A2+ B2+2AB Cos(180 – Θ) ]1/2 and
tanβ = B Sin(180 – Θ)/ [ A + B Cos(180 – Θ) ], Where Θ is the angle between A and B and β is the angle which R makes with the direction of A.
(iii) Vector subtraction is not commutativ (→A – →B) ≠ (→B – →A)
(iv) Vector subtraction is not associative,
Rectangular components of a vector in a plane :- If A makes an angle Θ with x-axis and Ax and By be the rectangular components of A along X-axis and Y- axis respectively, then
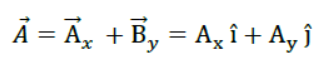
Here Ax = A CosΘ and Ay = A SinΘ
And A = ( Ax2 + Ay2)1/2
And tanΘ = Ay/Ax
Dot product or scalar product : – The dot product of two vectors A and B,
represented by .→A .→B is a scalar , which is equal to the product of the magnitudes of A and B and the Cosine of the smaller angle between them.
If Θ is the smaller angle between A and B, then
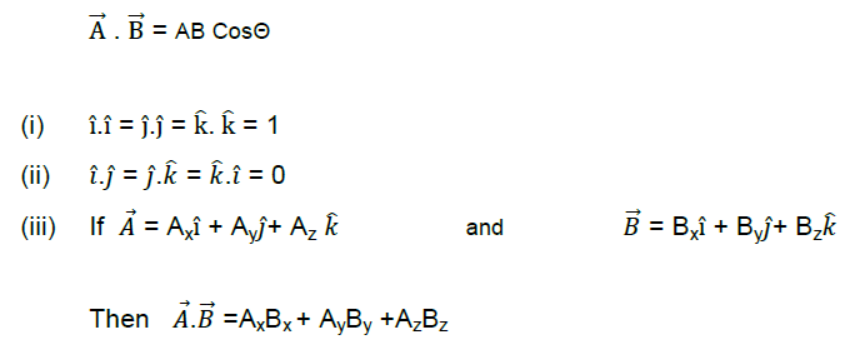
Cross or Vector product :-
The cross product of two vectors →A and →B , represented by→A x→B is a vector , which is equal to the product of the magnitudes of A and B and the sine of the smaller angle between them.
If Θ is the smaller angle between A and B, then
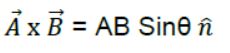

Projectile motion : – Projectile is the name given to anybody which once thrown in to space with some initial velocity, moves thereafter under the influence of gravity alone without being propelled by any engine or fuel. The path followed by a projectileis called its trajectory.
- Path followed by the projectile is parabola.
- Velocity of projectile at any instant t ,
V = [(u2 – 2ugtsin θ + g2t2)]1/2 - Horizontal range
R = u2 Sin2Θ/g
For maximum range Θ =450,
Rmax = u2 /g - Flight time
T = 2u SinΘ/g - Height
H = u2 sin2Θ/2g
For maximum height Θ =900
Hmax.= u2/2g
Very Short answer :
Question. Two balls of different masses are thrown vertically upward with same initial velocity. Height attained by them are h1 and h2 respectively what is h1/h2.
Answer: 1/1, because the height attained by the projectile is not depend on the masses.
Question. State the essential condition for the addition of the vector.
Answer: They must represent the physical quantities of same nature.
Question. What is the angle between velocity and acceleration at the peak point of the projectile motion ?
Answer: 90 0 .
Question. What is the angular velocity of the hour hand of a clock ?
Answer: W = 2π/12 = π/6 rad h-1,
Question. What does the slope of v-t graph indicate ?
Answer: Acceleration
Question. Under what condition the average velocity equal to instantaneous velocity?
Answer: For a uniform velocity.
Question. The position coordinate of a moving particle is given by x=6+18t+9t2 (x in meter, t in seconds) what is it’s velocity at t=2s
Answer: 54 m/sec.
Question. Give an example when a body moving with uniform speed has acceleration.
Answer: In the uniform circular motion.
Question. What is the source of centripetal acceleration for earth to go round the sun ?
Answer: Gravitation force of the sun.
Question. What is the average value of acceleration vector in uniform circular motion .
Answer: Null vector .
Question. Derive an equation for the distance travelled by an uniform acceleration body in nth second of its motion.
Answer: S Sn = u +a/2( 2n- 1)
Question.what is relative velocity in one dimension, if VA and VB are the velocities of the body A and B respectively then prove that VAB=VA-VB?
Answer: Relative Motion:- The rate of change of separation between the two object is called relative velocity. The relative velocity of an object B with respect to the object A when both are in motion is the rate of change of position of object B with respect to the object A .
*Relative velocity of object A with respect to object B
VAB = VA – VB
When both objects are moving in same direction , then the relative velocity of object
B with respect to the object A
VBA = VB – VA
Question. The velocity of a moving particle is given by V=6+18t+9t2 (x in meter, t in seconds) what is it’s acceleration at t=2s
Answer: Differentiation of the given equation eq. w.r.t. time
We get a = 18 + 18t
At t = 2 sec.
a= 54 m/sec2.
Question. Show that when the horizontal range is maximum, height attained by the body is one fourth the maximum range in the projectile motion.
Answer: We know that the horizontal range
R = u2 Sin2Θ/g
For maximum range Θ =450,
Rmax = u2 /g
and Height
H = u2 sin2Θ/2g
For Θ =450
H = u2 /4g = 1/4 of the Rmax.
Question. Derive the relation between linear velocity and angular velocity
Answer: Derive the expression
V = r ω
Question. The greatest height to which a man can a stone is h, what will be the longest distance upto which he can throw the stone ?
Answer: we know that
Hmax.= Rmax /2
So h = R/2
Or R = 2h
Question. State the parallelogram law of vector addition. Derive an expression for magnitude and direction of resultant of the two vectors.
Answer: The addition of two vector →A and→B is resultant→R
And R = ( A2 + B2+ 2AB CosΘ)1/2
And tan β = B SinΘ/ ( A + B CosΘ) ,
Where Θ is the angle between vector →A and vector →B , And β is the angle which→R makes with the direction of .
Question. A gunman always keeps his gun slightly tilted above the line of sight while shooting. Why,
Answer: Because bullet follow parabolic trajectory under constant downward acceleration.
HOTS Question :
Question.→A and→B are two vectors and Θ is the angle between them, If

Answer: 60 0
Question. A boat is sent across a river with a velocity of 8km/h. if the resultant velocity of boat is 10 km/h , then calculate the velocity of the river.
Answer: 6 km/h.
Question. A cricket ball is hit at 450 to the horizontal with a kinetic energy E. calculate the kinetic energy at the highest point.
Answer: E/2.(because the horizontal component uCos450 is present on highest point.)
Question. Speed of two identical cars are u and 4u at a specific instant. The ratio of the respective distances at which the two cars stopped from that instant.
Answer: 1 : 16
Question. A projectile can have the same range R for two angles of projection. If t1 and t2 be the time of flight in the two cases, then prove that t1t2 = 2R/g
Answer: for equal range the particle should either be projected at an angle Θ and (90 – Θ) ,then t1 = 2u SinΘ/g
t2 = 2u Sin(90 – Θ)/g = 2u CosΘ/g
t1t2 = 2R/g .
We hope the above Kinetic Theory Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


