Please refer to Thermodynamics Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Thermodynamics Notes and Questions
- Thermal Equilibrium:- Two systems are said to be in thermal equilibrium with each other if they have the same temperature.
- Thermo dynamical system:- An assembly of large numbers of particles having same temperature, pressure etc is called thermo dynamical system.
- Thermodynamic variables :- The variables which determine the thermodynamic behavior of a system are called thermodynamic variables
- Zeroth law of Thermodynamics :- IT states that if two system A and B are in thermal equilibrium with a third system C , then the two system A and B are also in thermal equilibrium with each other.
- Thermodynamic Process :- A thermodynamic process is said to be taking place , if the thermodynamic variable of the system change with time.
Types of thermodynamic Process:-
(1) Isothermal process – process taking place at constant temperature.
(2) Adiabatic process – process where there is no exchange of heat.
(3) Isochoric process – process taking place at constant volume
(4) Isobaric process –Process taking place at constant Pressure.
(5) Cyclic process:- Process where the system returns to its original state.
- Equation of state : A relation between pressure, volume and temperature for a system is called its equation of state .
- Indicator diagram (P-V diagram) :- The graphical representation of the state of a system with the help of two thermodynamical variables is called indicator diagram of the system.
- Internal energy of a gas :- It is the sum of kinetic energy and the intermolecular potential energy of the molecules of the gas. Internal energy is a function of temperature.
- First law of Thermodynamics :- It states that if an amount of heat dQ I added to a system , a part of heat is used in increasing its internal energy while the remaining part of heat may be used up as the external work done dW by the system.
Mathematically dQ=dU+dW
dQ=dU+ PdV.
- Work done during expansion / compression of gas:- When the volume of gas changes from V1 to V2 , the work done is given by W= ∮ v2/v1 pdv = Area under the P -V diagram.
- Thermodynamical operations are
(1) Isothermal process : A thermodynamic process that takes place at constant temperature is called an isothermal process.
– Equation of state for isothermal process : PV = constant.
– Work done during an isothermal process
Wiso = RT loge v2/v1 = 2.303 RT loge v2/v1
(2) Adiabatic process : A thermodynamic process that takes place in such a manner that no heat enters or leaves the system is called adiabatic process
- Equation of state for adiabatic process
(i) PV γ = constant (ii) TV γ-1 =constant - -py-1/Ty = constant
- Work done during adiabatic change Wadia = R(T1-T2)/(y-1)
- Reversible process :- It is a process in which the system can be retraced to its original state by reversing the condiditions.
- Irreversible process:- It is a process in which the system cannot be retraced to its original state by reversing the conditions.
- Second law of thermodynamics:
- Kelvin’s statement of second law – It is impossible to derive a continous supply of work by cooling a body to a temperature lower than that of the coldest of its surrounding.
- Clausius statement of second law – It is impossible for a self –acting machine unaided by any external agency to transfer heat from a body to another body at higher temperature.
- Heat Engine – a heat engine is a device for converting heat energy continuously into a mechanical work.
- Component of heat engine- (i) source of heat (ii) Sink (iii) Working substance
- Efficiency of heat Engine :- It is defined as the ratio of the external work obtained to the amount of heat energy absorbed from the heat source.
- Mathematically ȵ = W/Q1 = Q1 – Q2/Q1 = 1 -Q2/Q1
- Carnot’s heat Engine :- it is an ideal heat Engine which is based on carnot’s reversible cycle.
- Efficiency of carnot’s heat Engine
- ȵ= 1 -Q2/Q1 = 1 – T2/T1
- Refrigerator or Heat pump:- it is heat engine working backward.
- Co-efficient of performance : It is the ratio of heat absorbed from cold body to the work done by the refrigerator.
Mathematically β =Q2/W = Q2/Q1 – Q2 = T2 /T1 – T2
HOTs Question
Question. What is the nature of P-V diagram for isobaric and isochoric process?
Answer : The P-V diagram for an isobaric process is a straight line parrel to the volume axis while that For an isochoric process is a straight line parallel to pressure axis.
Question. On what factors does the efficiency of Carnot engine depends?
Answer : Temperature of the source of heat and sink.
Question. The temperature T1 and T2 of two heat reserviour in an ideal carnot engine are 1500oC and 500oC. Which of this increasing the temperature T1 by 100oC or decreasing T2 by 100oC would result in greater improvement of the efficiency of the engine?
Answer : Using ¶ =1 –T2/T1 =(T1– T2)/T1
(1) increasing T1 by 100oC ¶1 = (1600 -500)/(1600 + 273 )
= 1100/1873 = 59 %
(ii) Decreasing T2 by 1000C ¶2 = 1500 –(500-100)/(1500 +273 )
=1100/1773 = 67%
Therefore decreasing T2 by 100oC results in greater improvement of efficiency.
Question. Can we increase the temperature of gas without supplying heat to it?
Answer : Yes, the temperature of gas can be by compressing the gas under Adiabatic condition.
Question. Why does the gas get heated on compression?
Answer : Because the work done in compressing the gas increases the internal energy of the gas.
Question. Which thermodynamic variable is defined by Zeroth law of thermodynamics?
Answer : Temperature
Question. Which Thermodynamical variable is defined by the first law of thermodynamics?
Answer : Internal energy.
Question. Assuming a domestic refrigerator as a reversible heat engine working between melting point Of ice and the room temperature at 27oC, calculate the energy in joule that must be supplied to freeze 1Kg of water at 0oC.
Answer : Here T1 = 27+273 =300K , T2 =0 +273 = 273
Mass of water to be freezed , M = 1 Kg = 1000g
Amount of heat that should be removed to freeze the water
Q2 = ML =1000X 80 cal
= 1000X80 X 4.2 =3.36 x 105 J
Now Q1 = (T1/T2 )X Q2 = (300/273)X3.36×105 = 3.692 x105 J
Therefore energy supplied to freeze the water
W =Q1 – Q2 = 3.693×105 – 3.36 x105
= 3.32 x105 J
Question. What is the amount of work done in the Cyclic process?
Answer : It is numerically equal to the area of the cyclic process.
Question. Out of the parameters- temperature, pressure,work and volume, which parameter does not Characterize the thermodynamics state of matter?
Answer : Work
Question. Can the whole of work be converted into heat?
Answer : Yes ,Through friction.
Question. In a Carnot engine, temperature of the sink is increased. What will happen to its efficiency?
Answer : We know ƞ = 1 – T2/T1
On increasing the temperature of the sink (T2), the efficiency of the Carnot engine will decrease
Question. Air pressure in a car increases during driving. Explain Why?
Answer : During driving as a result of the friction between the tyre and road ,the temperature of
The tyre and the air inside it increases. Since volume of the tyre does not change, due to increase in temperature ,pressure of the increases (due to pressure law ).
Question. Calculate the fall in temperature when a gas initially at 720C is expanded suddenly to eight times its original volume. Given γ= 5/3.
Answer : Let V1 = x cc V2 =8x cc
T1 =273+72 =345 K ¥ = 5/3 , T2 = ?
Using the relation T1 V1 ¥-1 = T2 V2 ¥-1
Therefore T2 = T1 (V1/V2)¥-1
=345x(1/8)2/3
Taking log of both sides, we get
Log T2 = log 345 – 2/3 log8
=2.5378 – 2/3(0.9031)
= 2.5378 -0.6020 = 1.9358
Or T2 =86.26 K
Therefore the fall in temperature = 345 -86.26 258.74 K
Question. The efficiency of a heat engine cannot be 100%. Explain why ?
Answer : The efficiency of heat engine ƞ = 1 –T2/T1
The efficiency will be 100% or 1, if T2 = 0 K.
Since the temperature of 0 K cannot be reached, a heat engine cannot have 100% efficiency.
Question. In an effort to cool a kitchen during summer, the refrigerator door is left open and the kitchen door and windows are closed. Will it make the room cooler ?
Answer : The refrigerator draws some heat from the air in front of it. The compressor has to do some Mechanical work to draw heat from the air at lower temperature. The heat drawn
from the air together with the work done by the compressor in drawing it, is rejected by the refrigerator with the help of the radiator provided at the back to the air. IT follows that in each cycle, the amount of heat rejected to the air at the back of the refrigerator will be greater than that is drawn from the air in front of it. Therefore temperature of the room will increase and make hotter.
Question. Why cannot the Carnot’s engine be realised in practice?
Answer : Because of the following reasons
(i) The main difficulty is that the cylinder should come in contact with the source,sink and stand again and again over a complete cycle which is very difficult to achieve in practice.
(ii) The working substance should be an ideal gas however no gas fulfils the ideal gas behaviour.
(iii) A cylinder with a perfectly frictionless piston cannot be realised
Question. A slab of ice at 273K and at atmospheric pressure melt.(a) What is the nature of work done on The ice water system by the atmosphere?(b)What happen to the internal energy of the ice- Water system?
Answer : (a) The volume of the ice decreases on melting. Hence the work done by the atmosphere on The ice – water system is positive in nature.
(b) Since heat is absorbed by the ice during melting, the internal energy of the icewater system increases.
Question. If hot air rises , why is it cooler at the top of mountain than near the sea level ? 2
Answer : Since atmospheric pressure decreases with height, pressure at the top of the mountain is lesser. When the hot air rises up,it suffer adiabatic expansion at the top of the mountain.For an adiabatic change,first law of thermodynamics may be express as
dU + dW =0 (dQ = 0)
dW = -dU
Therefore work done by the air in rising up (dW =+ve ) result in decrease in the internal Energy of the air (dU = -ve) and hence a fall in the temperature.
Question. What happen to the internal energy of a gas during (i) isothermal expansion (ii) adiabatic Expansion?
Answer : In isothermal expansion ,temperature remains constant.Therefore internal energy which is a function of temperature will remain constant.
(ii) for adiabatic change dQ = 0 and hence first law of thermodynamics becomes
0 = dU + dW
dW = – dU
During expansion, work is done by the gas i.e. dW is positive. Hence ,dU must be negative.
Thus ,in an adiabatic expansion , the internal energy of the system will decrease.
Question. Why is the conversion of heat into work not possible without a sink at lower temperature?
Answer : For converting heat energy into work continuosly, a part of the heat energy absorbed from the source has to be rejected.The heat energy can be rejected only if there is a body whose Temperature is less than that of the source. This body at lower temperature is called sink.
Question. Can water be boiled without heating ?
Answer : Yes, water can be boil without heating. This is done by increasing the pressure on the surface of water inside a closed insulated vessel. By doing so, the boiling point of the water decreases to the room temperature and hence starts boiling.
Question. What are the limitations of the first law of thermodynamics ?
Answer : The limitations are —
(i) It does not tells us the directions of heat transfer
(ii) it does not tell us how much of the heat is converted into work.
(iii) it does not tell us under what conditions heat is converted into work.
Question. A Carnot engine whose source temperature is at 400K takes 100 Kcal of heat at this temperature in each cycle and gives 70 Kcal to the sink. Calculate (i) the temperature of the sink (ii) the efficiency of the engine.
Answer : Here T1 =400K , Q1 = 100 Kcal , Q2 = 70 Kcal
T2 = ? ,¶ = ?
(i) Q1/Q2 = T1/T2
Or T2 = (Q2/Q1)T1
Or T2 =70/100 x400
Or T2 = 280 K
(ii) ƞ= 1- T2/T1
= 1 – 280/400
= 1- 0.7 = 0.3
Or % of ƞ= 0.3 x100 =30 %
Question. If at 50oC and 75 cm of mercury pressure, a definite mass of gas is compressed (i)slowly
(iii) suddenly, then what will be the final pressure and temperature of the gas in each case, if the final volume is one fourth of the initial volume? Given γ = 1.5
Answer : (I) When the gas is compressed slowly, the change is isothermal.
Therefore P2 V2 =P1 V1
P2 = P1V1/V2
=(75x V1/V 1 )x4 = 300 cm of mercury
Temperature remains constant at 50oC
(ii) When the gas is compressed suddenly, the change is adiabatic
As per P2 V2 γ = P1 V1
P2 = P1(V1/V2)γ
= 75 x (4)1.5 =600 cm of Hg
Also T2 V2 ¥-1 = T1 V1 ¥-1
T2 = T1 (V1/V2)¥-1 = 323x(4)(1.5- 1) = 646K
=646-273 =373 oC
Question. Two engines A and B have their sources at 400K and 350 K and sink at350K and 300K Respectively. Which engine is more efficient and by how much?
Answer : For engine A T1 =400K , T2 = 350 K
Efficiency ƞA =1 –T2/T1
=1-350/400 =1/8
% of ƞA = 1/8 X100 = 12.5%
For Engine B T1 = 350 K , T2 = 300 K
Efficiency ƞB = 1 – T2/T1
= 1- 300/350 =1/7
% of ƞB =1/7 x100 =14.3%
Since ƞB > ƞA so engine A is much more efficient than engine B by (14.3% – 12.5% ) = 1.8%
Question. A refrigerator freezes 5Kg of water at 0oC into ice at 0oc in a time interval of 20 minutes. Assume that the room temperature is 20oC, calculate the minimum power needed to accomplish it.
Answer : Amount of heat required to convert water into ice at 0oC,
Q2 =mL =(5Kg)x(80)Kcal/Kg
= 400 Kcal
Now T1 =20oC =273+20 = 293K
T2 = 0oc 0+273 =273 K
We know that Q2/W = T2/(T1 – T2 )
Or W = Q2 x (T1 – T2)/T2
= 400x(293- 273 )/273
= 29.3 Kcal = 29.3×4.2 x103J
=123×103 J
Time t = 20 min =20×60 =1200s
Power needed P = W/t =123×103/1200
=102.5 W
The branch of physics which deals with the study of transformation of heat energy into other forms of energy and vice-versa.
A thermodynamical system is said to be in thermal equilibrium when macroscopic variables (like pressure, volume, temperature, mass, composition etc) that characterise the system do not change with time.
Thermodynamical System
An assembly of an extremely large number of particles whose state can be expressed in terms of pressure, volume and temperature, is called thermodynamic system.
Thermodynamic system is classified into the following three systems
(i) Open System It exchange both energy and matter with surrounding.
(ii) Closed System It exchanges only energy (not matter) with surroundings.
(iii) Isolated System It exchanges neither energy nor matter with the surrounding.
A thermodynamic system is not always in equilibrium. For example, a gas allowed to expand freely against vacuum. Similary, a mixture of petrol vapour and air, when ignited by a spark is not an equilibrium state. Equilibrium is acquired eventually with time.
Thermodynamic Parameters or Coordinates or Variables
The state of thermodynamic system can be described by specifying pressure, volume, temperature, internal energy and number of moles, etc. These are called thermodynamic
parameters or coordinates or variables.
Work done by a thermodynamic system is given by
W = p * ΔV
where p = pressure and ΔV = change in volume.
Work done by a thermodynamic system is equal to the area enclosed between the p-V curve and the volume axis

Work done in process A-B = area ABCDA
Work done by a thermodynamic system depends not only upon the initial and final states of the system but also depend upon the path followed in the process.
Work done by the Thermodynamic System is taken as
Positive → 4 as volume increases.
Negative → 4 as volume decreases.
Internal Energy (U)
The total energy possessed by any system due to molecular motion and molecular configuration, is called its internal energy.
Internal energy of a thermodynamic system depends on temperature. It is the characteristic property of the state of the system.
Zeroth Law of Thermodynamics
According to this law, two systems in thermal equilibrium with a third system separately are in thermal equilibrium with each other. Thus, if A and B are separately in equilibrium with C, that is if TA = TC and TB = TC, then this implies that TA = TB i.e., the systems A and B are also in
thermal equilibrium.
First Law of Thermodynamics
Heat given to a thermodynamic system (ΔQ) is partially utilized in doing work (ΔW) against the surrounding and the remaining part increases the internal energy (ΔU) of the system.
Therefore, ΔQ = ΔU + ΔW
First law of thermodynamics is a restatement of the principle conservation of energy.
In isothermal process, change in internal energy is zero (ΔU = 0).
Therefore, ΔQ = ΔW
In adiabatic process, no exchange of heat takes place, i.e., Δθ = O.
Therefore, ΔU = – ΔW
In adiabatic process, if gas expands, its internal energy and hence, temperature decreases and vice-versa.
In isochoric process, work done is zero, i.e., ΔW = 0, therefore
ΔQ = ΔU
Thermodynamic Processes
A thermodynamical process is said to take place when some changes’ occur in the state of a thermodynamic system i.e., the therrnodynamie parameters of the system change with time.
(i) Isothermal Process A process taking place in a thermodynamic system at constant temperature is called an isothermal process.
Isothermal processes are very slow processes.
These process follows Boyle’s law, according to which
pV = constant
From dU = nCvdT as dT = 0 so dU = 0, i.e., internal energy is constant.
From first law of thermodynamic dQ = dW, i.e., heat given to the system is equal to the work done by system surroundings.
Work done W = 2.3026μRT l0g10(Vf / Vi) = 2.3026μRT l0g10(pi / pf)
where, μ = number of moles, R = ideal gas constant, T = absolute temperature and Vi Vf and Pi, Pf are initial volumes and pressures.
After differentiating P V = constant, we have
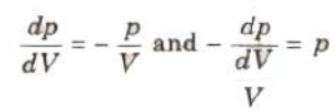
i.e., bulk modulus of gas in isothermal process, β = p.
P – V curve for this persons is a rectangular hyperbola
Examples
(a) Melting process is an isothermal change, because temperature of a substance remains constant during melting.
(b) Boiling process is also an isothermal operation.
(ii) Adiabatic Process A process taking place in a thermodynamic system for which there is no exchange of heat between the system and its surroundings.
Adiabatic processes are very fast processes.
These process follows Poisson’s law, according to which

From dQ = nCdT, Cadi = 0 as dQ = 0, i.e., molar heat capacity for adiabatic process is zero.
From first law, dU = – dW, i.e., work done by the system is equal to decrease in internal energy. When a system expands adiabatically, work done is positive and hence internal energy
decrease, i.e., the system cools down and vice-versa.
Work done in an adiabatic process is

where Ti and Tf are initial and final temperatures. Examples
(a) Sudden compression or expansion of a gas in a container with perfectly non-conducting wall.
(b) Sudden bursting of the tube of a bicycle tyre.
(c) Propagation of sound waves in air and other gases.
(iii) Isobaric Process A process taking place in a thermodynamic system at constant pressure is called an isobaric process.
Molar heat capacity of the process is Cp and dQ = nCpdT.
Internal energy dU = nCv dT
From the first law of thermodynamics
dQ = dU + dW
dW = pdV = nRdT
Process equation is V / T = constant.
p- V curve is a straight line parallel to volume axis.
(iv) Isochoric Process A process taking place in a tlaermodynars system at constant volume is called an isochoric process.
dQ = nCvdT, molar heat capacity for isochoric process is Cv.
Volume is constant, so dW = 0,
Process equation is p / T = constant
p- V curve is a straight line parallel to pressure axis.
(v) Cyclic Process When a thermodynamic system returns to . initial state after passing through several states, then it is called cyclic process. Efficiency of the cycle is given by

Work done by the cycle can be computed from area enclosed cycle on p- V curve.
Isothermal and Adiabatic Curves
The graph drawn between the pressure p and the volume V of a given mass of a gas for an isothermal process is called isothermal curve and for an adiabatic process it is called adiabatic curve .

The slope of the adiabatic curve
= γ x the slope of the isothermal curve
Volume Elasticities of Gases
There are two types of volume elasticities of gases
(i) Isothermal modulus of elasticity ES = p
(ii) Adiabatic modulus of elasticity ET = γ p
Ratio between isothermal and adiabatic modulus
ES / ET = γ = Cp / CV
where Cp and Cv are specific heats of gas at constant pressure and at constant volume.
For an isothermal process Δt = 0, therefore specific heat,
c = Δ θ / m Δt = &infi;
For an adiabatic process 119= 0, therefore specific heat,
c = 0 / m Δt = 0
Second Law of Thermodynamics
The second law of thermodynamics gives a fundamental limitation to the efficiency of a heat engine and the coefficient of performance of a refrigerator. It says that efficiency of a heat
engine can never be unity (or 100%). This implies that heat released to the cold reservoir can never be made zero.
Kelvin’s Statement
It is impossible to obtain a continuous supply of work from a body by cooling it to a temperature below the coldest of its surroundings.
Clausius’ Statement
It is impossible to transfer heat from a lower temperature body to a higher temperature body without use of an extemal agency.
Planck’s Statement
It is impossible to construct a heat engine that will convert heat completely into work.
All these statements are equivalent as one can be obtained from the other.
Entropy
Entropy is a physical quantity that remains constant during a reversible adiabatic change.
Change in entropy is given by dS = δQ / T Where, δQ = heat supplied to the system and T = absolute temperature.
Entropy of a system never decreases, i.e., dS ≥ o.
Entropy of a system increases in an irreversible process
Heat Engine
A heat energy engine is a device which converts heat energy into mechanical energy.
A heat engine consists of three parts
(i) Source of heat at higher temperature
(ii) Working substance
(iii) Sink of heat at lower temperature
Thermal efficiency of a heat engine is given by

where Q1 is heat absorbed from the source, Q2 is heat rejected to the sink and T1 and T2 are temperatures of source and sink.
Heat engine are of two types
(i) External Combustion Engine In this engine fuel is burnt a chamber outside the main body of the engine. e.g., steam engine. In practical life thermal efficiency of a steam engine varies from 12% to 16%.
(ii) Internal Combustion Engine In this engine. fuel is burnt inside the main body of the engine. e.g., petrol and diesel engine. In practical life thermal efficiency of a petrol engine is 26% and a diesel engine is 40%.
Carnot’s Cycle
Carnot devised an ideal cycle of operation for a heat engine, called Carnot’s cycle.

A Carnot’s cycle contains the following four processes
(i) Isothermal expansion (AB)
(ii) Adiabatic expansion (BO)
(iii) Isothermal compression (CD)
(iv) Adiabatic compression (DA)
The net work done per cycle by the engine is numerically equal to the area of the loop representing the Carnot’s cycle .
After doing the calculations for different processes we can show that

[Efficiency of Carnot engine is maximum (not 1000/0) for given temperatures T1 and T2. But still Carnot engine is not a practical engine because many ideal situations have been assumed while designing this engine which can practically not be obtained.]
Refrigerator or Heat Pump
A refrigerator or heat pump is a device used for cooling things. It absorb heat from sink at lower temperature and reject a larger amount of heat to source at higher temperature.
Coefficient of performance of refrigerator is given by

where Q2 is heat absorbed from the sink, Q1 is heat rejected to source and T1 and T2 are temperatures of source and sink.
Relation between efficiency (η) and coefficient of performance (β)


We hope the above Thermodynamics Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


