Check the below NCERT MCQ Class 12 Mathematics Chapter 7 Integrals with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Integrals Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Integrals Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 7 Integrals with solutions. Solve questions and compare with the answers provided below
Question. The value of
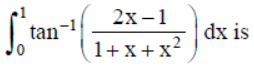
(a) 1
(b) 0
(c) – 1
(d) π/4
Answer
B
Question. Evaluate:
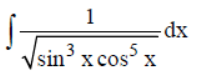
(a) 2/tan x – 2/3 (tan x)3/ 2 + C
(b) -2/tan x + 2/3 (tan x)3/ 2 + C
(c) – 2/tan x – 2/3 (tan x)3/ 2 + C
(d) None of these
Answer
B
Question.
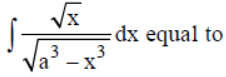
(a) 1/3 sin-1 √x3/a3 + C
(b) 2/3 sin-1 √x3/a3 + C
(c) 2/3 sin-1 √x/a + C
(d) None of these
Answer
B
Question. The value of
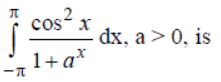
(a) π
(b) a π
(c) π/2
(d) 2 π
Answer
C
Question.
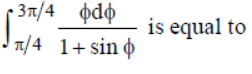
(a) √2-1
(b) 1/√2-1
(c) π/√2+1
(d) π/√2-1
Answer
C
Question. Evaluate:
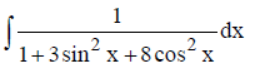
(a) 1/6 tan-1 (2 tan x) + C
(b) tan-1(2 tan x) + C
(c) 1/6 tan-1 (2 tan x/3) + C
(d) None of these
Answer
C
Question. Consider the following statements
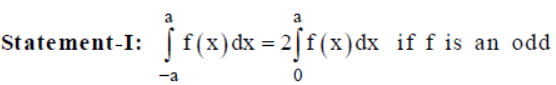
if f (– x) = f (x).
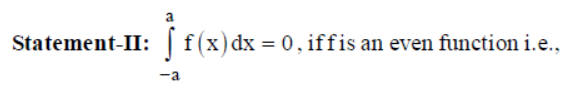
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
D
Question. Value of
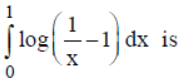
(a) 2I
(b) –2I
(c) 0
(d) None of these
Answer
C
Question. Evaluate:
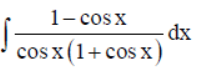
(a) log | sec x + tan x | – 2 tan (x / 2) + C
(b) log | sec x – tan x | – 2tan (x / 2) + C
(c) log | secx + tan x | + 2 tan(x / 2) + C
(d) None of these
Answer
A
Question.
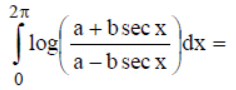
(a) 0
(b) π/2
(c) π(a+b)/a-b
(d) π/2 (a2-b2)
Answer
A
Question. Evaluate: ∫ sin3 x cos3 x dx
(a) 1/32 {3/2 cos 2x – 1/6 cos 6x } + C
(b) 1/32{-3/2 cos 2x + 1/6 cos 6x } + C
(c) 1/32{-3/2 cos 2x -1/6 cos 6x } + C
(d) None of these
Answer
B
Question. If f(x) =
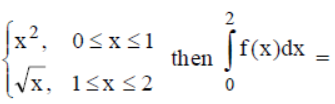
(a) 1/3
(b) 4 √2
(c) 4 √2 -1
(d) None of these
Answer
D
Question.
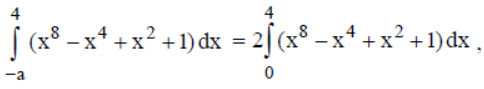
then a =
(a) 3
(b) 4
(c) 6
(d) 8
Answer
B
Question.
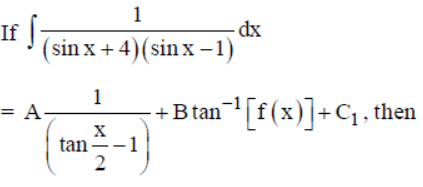
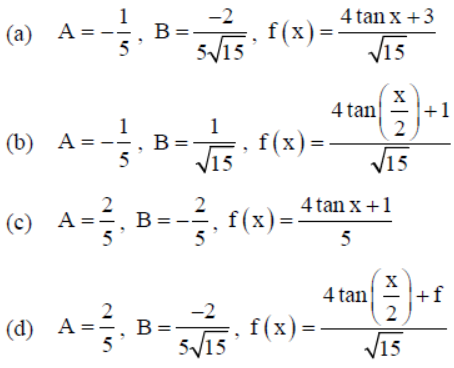
Answer
D
Question. If
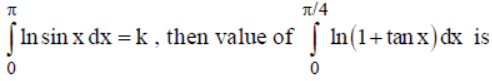
(a) -k/4
(b) k/4
(c) -k/8
(d) k/8
Answer
C
Question. Value of
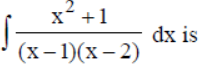
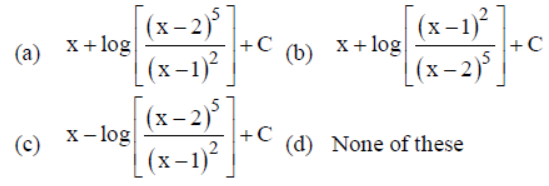
Answer
A
Question.
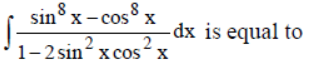
(a) 1/2 sin 2x + c
(b) -1/2 sin 2x + c
(c) -1/2 sin 2x + c
(d) -sin 2 x + c
Answer
B
Question. Evaluate:
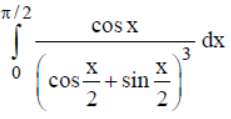
(a) 2 – √2
(b) 2 + √2
(c) 3 + √3
(d) 3 – √3
Answer
A
Question. Evaluate:
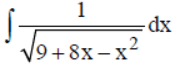
(a) -sin-1(x-4/5) + C
(b) -sin-1(x+4/5) + C
(c) sin-1(x-4/5) + C
(d) None of these
Answer
C
Assertion and Reason type Questions:
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion : If d/dx ∫ f(x) dx = f(x) , then ∫f (x) dx = f’ (x) + C where C is an arbitrary constant.
Reason : Process of differentiation and integration are inverses of each other.
Answer
D
Question. Assertion : Geometrically, derivative of a function is the slope of the tangent to the corresponding curve at a point.
Reason : Geometrically, indefinite integral of a function represents a family of curves parallel to each other.
Answer
B
Question. Assertion :
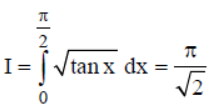
Reason: tan x = t2 makes the integrand in I as a rational function.
Answer
A
Question. Assertion : The value of
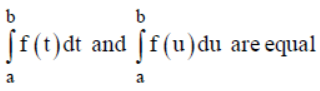
Reason : The value of definite integral of a function over any particular interval depends on the function and the interval not on the variable of integration.
Answer
A
Question. Assertion : If the derivative of function x is d/dx (x) = 1 , then its anti-derivatives or integral is ∫(1)dx = x + C .
Reason : If d/dx (xn+1/n+1) = xn , then the corresponding integral of the function is
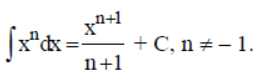
Answer
A
Question. Assertion : The value of the integral ∫ ex ex[tan x + sec2 x]dx is ex tan x + C .
Reason : The value of the integral ex {f(x) + f'(x)} dx is ex f (x) + C.
Answer
A
Question. Assertion
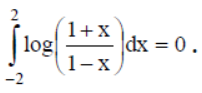
Reason : If f is an odd function, then
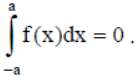
Answer
A
Question. Assertion : Derivative of a function at a point exists.
Reason : Integral of a function at a point where it is defined, exists.
Answer
C
Question. Assertion: It is not possible to find
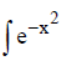
dx by inspection method.
Reason : Function is not expressible in terms of elementary functions.
Answer
A
Question. Assertion :
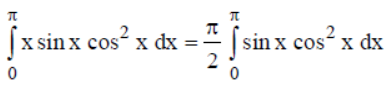
Reason :
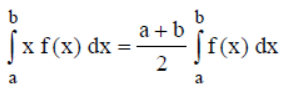
Answer
C
Question. Assertion : ∫ [sin(logx)+cos(logx)]dx = x sin (log x) + C .
Reason : d/dx [x sin (log x)] = sin (log x) + cos(log x).
Answer
A
