MCQ Questions for Class 10 Introduction to Trigonometry with Answers

Students can refer to the following Trigonometry Class 10 MCQ Question with Answers provided below based on the latest curriculum and examination pattern issued by CBSE and NCERT. Our teachers have provided here a collection of multiple choice questions for Trigonometry Class 10 covering all topics in your textbook so that students can assess themselves on all important topics and thoroughly prepare for their exams

Trigonometry Class 10 MCQ Question with Answers

We have provided below chapter-wise Trigonometry Class 10 MCQ Question with answers which will help the students to go through the entire syllabus and practice multiple choice questions provided here with solutions. As Trigonometry MCQs in Class 10 pdf download can be really scoring for students, you should go thorough all problems and MCQ Questions for Class 10 Maths provided below so that you are able to get more marks in your exams.

Question. What is the value of sin² 5^o + sin² 10^o + sin² 80^o + sin² 85^o ?
(a) 0
(b) 1
(c) 2
(d) 3

Question. If tan 26^o tan19^o/ x(1 tan 26^o tan19^o ) = cos60^o, what is the value of x ?
(a) 1
(b) 2
(c) 2
(d) 3

Question. If 4tanΘ = 1, find the value of 4sinΘ – 2cosΘ / 4sinΘ + 3cosΘ
(a) 1/2
(b) 1/6
(c) 2/3
(d) 1/3

Question. Find the value of 5cos α – 4 / 3 + 5sin α / 3 – 5sin α / 4 + 5cos α
(a) – 1
(b) 5
(c) 1
(d) 0

Question. If sin A + sin2 A = 1 , find the value of the expression (cos2 A + cos4 A) .
(a) 1
(b) 1/2
(c) 2
(d) 3

Question. Find the value of sin 15^o .
(a) √3+1/√2
(b) √3 -1/√2
(c) √3+1/2√2
(d) √3 -1/2√2

Question. Find the value sin² 30^o cos² 45^o + 4tan² 30^o + 1/2 sin² 90o 2cos² 90^o + 1/24
(a) 1
(b) 2
(c) √2
(d) √3

Question. An electric pole is 10√3 m high and its shadow is 10 m in length, then the angle of elevation of the sun is 
(a) 45°
(b) 15°
(c) 30°
(d) 60°

Question. A kite is flying at a height of 90 m above the groun(d) The string attached to the kite is temporarily tied to a point on the groun(d) The inclination of the string with the ground is 60° . The length of the string, assuming that there is no slack in the string is     
(a) 90√3 m
(b) 60√3 m
(c) 90 m
(d) 45 m

Question. If the angle of depression of a car from a 100 m high tower is 45°, then the distance of the car from the tower is   
(a) 100 m
(b) 200 m
(c) 100√3m
(d) 100√2m

Question. A kite is flying at a height of 200 m above the groun(d) The string attached to the kite is temporarily tied to a point on the groun(d) The inclination of the string with the ground is 45°. The length of the string, assuming that there is no slack in the string is   
(a) 100 m
(b) 200 m
(c) 200√2 m
(d) 100√2 m

Question. The _____________ is the line drawn from the eye of an observer to the point in the object viewed by the observer.     
(a) Horizontal line
(b) line of sight
(c) None of these
(d) Vertical line

Question. A pole 10 m high cast a shadow 10 m long on the ground, then the sun’s elevation is     
(a) 60°
(b) 15°
(c) 45°
(d) 30°

Question. Find sin³ φ + cos³ φ/sin φ + cos φ .
(a) 1 + sin – cos φ
(b) 1- sinc φ cos φ
(c) 1- sin φ tan φ
(d) 1

Question. lf sinθ + cosθ/sinθ – cosθ = √3 + 1/√3 – 1 find the acute angleθ .
(a) 90°
(b) 45°
(c) 30°
(d) 60°

Question. What is the value of θ tor which tanθ = cotθ ?
(a) 60°
(b) 45°
(c) 90°
(d) 0°

Question. The figure shows an isosceles triangle ABC. Find the length of the perpendicular from A to BC.

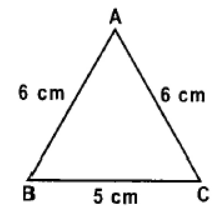
(a) 5.45 cm
(b) 4.55 cm
(c) 5.6 cm
(d) 4.54 cm

Question. What is the value of sinθ + cos30° – tan45°+ cosec 60° + cot90° ?
(a) 7√3 – 6/6
(b) 6 + 7√3/6
(c) 0
(d) 2

Question. If sin θ = 1/2 , what are the respective possible values of 9 between 0 and 2π ?
(a) 210° and 300°
(b) 240° and 330°
(c) 240° and 300°
(d) 210° and 330°

Question. In terms of radians. what is the equivalent of 45° ?
(a) 25π
(b) 0.25π
(c) 180°π /45°
(d) 45°/π

Question. ΔABC is right angled at A. If AC = 8 cm and AB = 6 cm, what is the value of cosec B?
(a) 5/4
(b) 3/4
(c) 4/3
(d) 4/5

Question. ΔABC is right angled at A .lf BC = √2 and AB = AC =1, what is the measure of ∠B ?
(a) 60°
(b) 45°
(c) 30°
(d) 90°

Question. Find the value of 5cos α – 4/3 – 5 sin α – 3 + 5 sin α/4 + 5 cos α .
(a) – 1
(b) 5
(c) 1
(d) 0

Question. Two men are on opposite sides of a tower. They observe the angles of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 100m, then the distance between them is   
(a) 100(√3−1) m
(b) 100(√3+1) m
(c) 100(1−√3) m
(d) none of these

Question. The ___________ is the angle between the horizontal and the line of sight to an object when the object is below the horizontal level.     
(a) angle of projection
(b) angle of elevation
(c) None of these
(d) angle of depression

Question. The ratio between the height and the length of the shadow of a pole is √3: 1, then the sun’s altitude is   
(a) 45°
(b) 30°
(c) 75°
(d) 60°

Question. The angle of elevation of the top of a tower from a point on the ground and at a distance of 30°m from its foot is . The height of the tower is   
(a) 30√3m
(b) 10 m
(c) 10√3m
(d) 30 m

Question. The ___________ of an object is the angle formed by the line of sight with the horizontal when the object is above the horizontal level.   
(a) angle of projection
(b) angle of depression
(c) angle of elevation
(d) none of these

Question. From a point on the ground which is 15m away from the foot of a tower, the angle of elevation is found to be 60° . The height of the tower is   
(a) 15√3 m
(b) 20√m
(c) 10√m
(d) 10 m

Question. From a point P on the level ground, the angle of elevation of the top of a tower is . If the tower is 100m high, the distance between P and the foot of the tower is   
(a) 300√3 m
(b) 150√3 m
(c) 200√3 m
(d) 100√3 m

Question. If the height of the tower is √3 times of the length of its shadow, then the angle of elevation of the sun is 
(a) 15°
(b) 30°
(c) 50°
(d) 45°

Question. A ramp for disabled people in a hospital must slope at not more than 30°. If the height of the ramp has to be 1 m, then the length of the ramp be   
(a) 3 m
(b) 1 m
(c) 2 m
(d) √3 m

Question. If the shadow of a boy ‘x’ metres high is 1.6m and the angle of elevation of the sun is then the value of ‘x’ is 45° 
(a) 0.8 m
(b) 1.6 m
(c) 3.2 m
(d) 2 m

Question. If the angle of depression of an object from a 75m high tower is 30° , then the distance of the object from the tower is   
(a) 25√3 m
(b) 50√3 m
(c) 100√3 m
(d) 75√3 m

Question. In a right triangle ABC, If AC = BC and then find its value     
(a) 50√3 
(b) 150 m
(c) None of these
(d) 100√3 m

Question. The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50m high, then the height of the hill is     
(a) 50√3 m
(b) 150m
(c) 150√3 m
(d) 100√3 m

Question. The angles of elevation of the top of a tower from two points on the ground at distances 8 m and 18 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is     
(a) 12 m   
(b) 18 m
(c) 8 m
(d) 16 m

Question. If cos9α = sinα a and 9α < 90^o, what is the value of tan 5 a?
(a) 1/√3
(b) √3
(c) 1
(d) 1/2

Question. ABCD is a trapezium in which AB = 8 cm, AD = 4 cm and CD = 3 cm. 

What is the length of BC to the nearest whole number?
(a) 5 cm
(b) √41cm
(c) 8 cm
(d) 7 cm

Question. Find the value of cos1^o cos2^o cos3^o …..cos89^o cos90^o
(a) 1
(b) 1/2
(c) 1/√2
(d) 0

Question. Find the value of 2/3 (cos⁴ 30^o – sin⁴ 45^o ) – 3 (sin² 60^o – sec² 45^o ) + 1/4 cot² 30^o
(a) 15/4
(b) 3/4
(c) 2(65/4)
(d) 4(17/24)

Question. If 8 tan A =15, find the value of sinA – cosA / sinA + cosA
(a) 7/23
(b) 11/23
(c) 13/23
(d) 17/23

Question. If 4sinΘ = 3cosΘ ,find sec²Θ / 4(1 – tan²Θ)
(a) 25/16
(b) 25/28
(c) 1/4
(d) 5/6

Question. If ΔABC is right angled at C, find the value of cos(A + B) .
(a) 0
(b) 1
(c) 1/2
(d) √3/2

Question. What is the value of sin² 5^o + sin² 10^o + sin² 80^o + sin² 85^o ?
(a) 0
(b) 1
(c) 2
(d) 3

Question. If tan 26^o tan19^o/ x(1 tan 26^o tan19^o ) = cos60^o, what is the value of x ?
(a) 1
(b) 2
(c) 2
(d) 3

Question. If 4tanΘ = 1, find the value of 4sinΘ – 2cosΘ / 4sinΘ + 3cosΘ
(a) 1/2
(b) 1/6
(c) 2/3
(d) 1/3

Question. If the shadow of a tower is 30 m long when the sun’s elevation is . The length of the shadow, when the sun’s elevation is     
(a) 10 m
(b) 30 m
(c) 10√3 m
(d) 20 m

Question. Two men are on opposite sides of a tower. They observe the angles of elevation of the top of the tower as 60° and 45° respectively. If the height of the tower is 60m, then the distance between them is   
(a) 20(√3−√3)m
(b) 20(√3−√3)m
(c) None of these
(d) 20(√3+√3)m

Question. A river is 60 m wide. A tree of unknown height is on one bank. The angle of elevation of the top of the tree from the point exactly opposite to the foot of the tree, on the other bank, is 30°. The height of the tree is   
(a) 30√3 m
(b) 10√3 m
(c) 20√3 m
(d) 60√3 m

Question. A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 30° there at. Its height above the ground is   
(a) 10 km
(b) 12 km
(c) 6 km
(d) none of these

Question. If the altitude of the sun is 60° , the height of a tower which casts a shadow of length 90 m is   
(a) 60 m
(b) 90√3 m
(c) 90 m
(d) 60√3 m

Question. Find the value of 5cos α – 4 / 3 + 5sin α / 3 – 5sin α / 4 + 5cos α
(a) – 1
(b) 5
(c) 1
(d) 0

Question. If sin A + sin2 A = 1 , find the value of the expression (cos2 A + cos4 A) .
(a) 1
(b) 1/2
(c) 2
(d) 3

Question. Find the value of sin 15^o .
(a) √3+1/√2
(b) √3 -1/√2
(c) √3+1/2√2
(d) √3 -1/2√2

Question. Find the value sin² 30^o cos² 45^o + 4tan² 30^o + 1/2 sin² 90o 2cos² 90^o + 1/24
(a) 1
(b) 2
(c) √2
(d) √3

Question. If cos9α = sinα a and 9α < 90^o, what is the value of tan 5 a?
(a) 1/√3
(b) √3
(c) 1
(d) 1/2

Question. ABCD is a trapezium in which AB = 8 cm, AD = 4 cm and CD = 3 cm. 

What is the length of BC to the nearest whole number?
(a) 5 cm
(b) √41cm
(c) 8 cm
(d) 7 cm

Question. Find the value of cos1^o cos2^o cos3^o …..cos89^o cos90^o
(a) 1
(b) 1/2
(c) 1/√2
(d) 0

Question. Find the value of 2/3 (cos⁴ 30^o – sin⁴ 45^o ) – 3 (sin² 60^o – sec² 45^o ) + 1/4 cot² 30^o
(a) 15/4
(b) 3/4
(c) 2(65/4)
(d) 4(17/24)

Question. If 8 tan A =15, find the value of sinA – cosA / sinA + cosA
(a) 7/23
(b) 11/23
(c) 13/23
(d) 17/23

Question. If 4sinΘ = 3cosΘ ,find sec²Θ / 4(1 – tan²Θ)
(a) 25/16
(b) 25/28
(c) 1/4
(d) 5/6

Question. If ΔABC is right angled at C, find the value of cos(A + B) .
(a) 0
(b) 1
(c) 1/2
(d) √3/2

Question. What is the angle between the hour and minute hands of a clock at 02 :15 hours?
(a) 15^o
(b) 7 (1^o/2)
(c) 22(1^o/2)
(d) 30^o

Question. What will be the change in the value of cosq if we decrease the value of θ? 

Question. What is the relation between sinθ,cosθ and cotθ? 

Question.If we increase the lengths of the sides of a right triangle keeping the angle between them same, then the values of the trigonometric ratios will also increase. State True or False. 

Question. Does the value of tanq increase or decrease as we increase the value of θ? Give reason.        

Question. What is the relation between tanq and secθ? 

Question. The value of tan A is always less than 1. State True or False. 

Question. Can the value of cos θ be 5/4 for some angle θ? 

Question. What is tan(90°-A) equal to? 

Question. What do we call the side opposite to the right angle in a right triangle?   

Question.  What is the reciprocal of sec A? 

Question. Is tan A the reciprocal of cot A?   

Question. Define an identity. 

Question. What is the maximum possible value for sine of any angle?   

Question. What is the value of sine of 0°?   

Question. What is 1+tan2θ? 

Question. What is the value of cosec 2θ -cot 2θ? 

Question. Name the side adjacent to angle A if DABC is a triangle right-angled at B.     

Question. Can the value of secant of an angle be greater than 1?        

Question If 2sin²θ -cos² θ = 2, then find the value of θ.

Question If cot θ = 7/8 check whether 1-tan²θ/1+tan²θ = cos²θ -sin²θ or not.

Question. Write True or False.

Question In ΔABC, if ∠A +∠C = 90°, then sin A = cosC     

Question cot 60° = tan (90° – 30°)   

Question The value of 2sinθ can be a+1/a, where a is a positive number and a ≠ 1.

QuestionsecA =1/cosA = 1 , for an acute θ   

Question sin60° = 2sin30°   

Question tanθ increases faster than sinθ as θ increases. 

Question If cot θ = 7/8 check whether 1-tan²θ/1+tan²θ = cos²θ -sin²θ or not.

Question sinθ +cosθ =1       

Question cos75° = cos60° +cos15°   

Question The value of the expression (sin70° -cos70°) is negative.   

Question If cosA+cos²A =1, then sin²A+sin⁴ A=1.    

Question If tan A = 3/4 , then cos A = 4/5   

Question tan² A = sec ² A -1 (v) sin² 56° +cos² 34° =1       

Question cosec 50° = sec 40°       

Question cos A = cos × A     

Question cosθ = 7/6 for some angleθ   

Question. Fill in the blanks.

Question sin A _____________ when A increases from 0° to 90°.

Question cos A _____________ when A increases from 0° to 90°.

Question cot 90° is ___________. 

Question If cosθ =1, then θ = ___________. 

Question sin58°/cos32° = _____________.

Question 3tan²45° = ___________.   

Question 5 cos 0° + sin 90° = ___________.

Question tan 0° = ___________. 

Question 2sin²45° = ___________.   

Question cos0° × cos10° × cos30° × cos80° × cos90° = _____________ .

Question The word ‘Trigonometry’ is derived from the Greek words _____________, _____________ and _____________.

Our teachers have developed really good Multiple Choice Questions covering all important topics in each chapter which are expected to come in upcoming tests and exams, as MCQs are coming in all exams now therefore practice them carefully to get full understanding of topics and get good marks. Download the latest questions with multiple choice answers for Class 10 Trigonometry in pdf or read online for free.

The above NCERT based Trigonometry Class 10 MCQ Question have been designed by our teachers in such a way that it will help you a lot to gain an understanding of each topic. These CBSE NCERT Class 10 Trigonometry Multiple Choice Questions have been developed and are available free for benefit of Class 10 students.

Advantages of Trigonometry Class 10 MCQ Question with Answers

a) MCQs will help the kids to strengthen concepts and improve marks in tests and exams.

b) Multiple Choice Questions for Trigonometry Class 10 have proven to further enhance the understanding and question-solving skills.

c) Regular reading topic wise questions with choices will for sure develop very good hold over each chapter which will help in exam preparations.

d) It will be easy to revise all Trigonometry chapters and faster revisions prior to class tests and exams.

Free Printable MCQs in PDF of CBSE Class 10 Trigonometry is designed by our school teachers and provide the best study material as per CBSE NCERT standards.