MCQ Questions For Class 10 Triangles

Students can refer to the following MCQ Questions for Class 10 Triangles with Answers provided below based on the latest curriculum and examination pattern issued by CBSE and NCERT. Our teachers have provided here a collection of multiple choice questions for Triangles Class 10 covering all topics in your textbook so that students can assess themselves on all important topics and thoroughly prepare for their exams

Class 10 Triangles MCQs Questions with Answers

We have provided below MCQs questions for Class 10 Triangles with answers which will help the students to go through the entire syllabus and practice multiple choice questions provided here with solutions. As Triangles MCQs in Class 10 pdf download can be really scoring for students, you should go through all problems provided below and MCQ Questions for Class 10 Maths so that you are able to get more marks in your exams.

Question. In the figure below, PQ || BC.

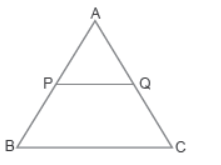
The ratio of the perimeter of triangle ABC to the perimeter of triangle APQ is 3:1. Given that the numerical value of the area of triangle APQ is a whole number, which of the following could be the area of the triangle ABC? 
(a) 28
(b) 60
(c) 99
(d) 120

Question. The ratio of the areas of two similar triangles, ABC and PQR shown below is 25 : 144. What is the ratio of their medians AM and PN?
(a) 5 : 12
(b) 5 : 16
(c) 12 : 5
(d) 25 : 144

Question. The ratio of the areas of two similar right triangles is 9 : 16. The length of one of the sides of the smaller triangle is 15 cm. How much longer is the length of the corresponding side of the larger triangle from smaller triangle?
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm

Question. If ΔDABC ~ ΔDDEF, (ar ΔABC )/ (ar ΔDEF )= 9/25, D D = , BC = 21 cm, then EF is equal to
(a) 9 cm
(b) 6 cm
(c) 35 cm
(d) 25 cm

Question. Observe the right triangle ABC, right angled at B as shown below.

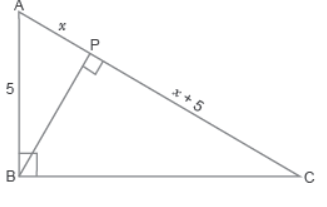
What is the length of PC? 
(a) 2.5 cm
(b) 4.5 cm
(c) 6 cm
(d) 7.5 cm

Question. Rohit is 6 feet tall. At an instant, his shadow is 5 feet long. At the same instant, the shadow of a pole is 30 feet long. How tall is the pole?
(a) 12 feet
(b) 24 feet
(c) 30 feet
(d) 36 feet

Question. Observe the right triangle ABC, right angled at A as shown below. If BP ⊥ AC, then which of the following is NOT correct? B A P C
(a) ΔAPB ~ ΔABC
(b) ΔAPB ~ ΔBPC
(c) BC² = CP . AC
(d) AC² = AB . CB

Question. D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 3 cm, BD = 5 cm, BC = 12.8 cm and DE || BC. Then length of DE (in cm) is
(a) 4.8 cm
(b) 7.6 cm
(c) 19.2 cm
(d) 2.5 cm

Question. Consider the figure below.
Mr Shah follows the below step to prove AB² + BC² = AC².
(i) ΔAPB ~ ΔABC (ii) AP/AB=AB/AC = (iii) AB² = AP . AC. 
Which of these could be his next step?
(a) Prove ΔABC ~ ΔPAB
(b) Prove ΔAPB ~ ΔCPB
(c) Prove ΔBPC ~ ΔABC
(d) Prove ΔAPB ~ ΔBPC

Question. Ankit is 5 feet tall. He places a mirror on the ground and moves until he can see the top of a building. At the instant when Ankit is 2 feet from the mirror, the building is 48 feet from the mirror. How tall is the building?
(a) 96 feet
(b) 120 feet
(c) 180 feet
(d) 240 feet

Question. Consider the following three clamis about a triangle ABC with side lengths m, n and r.
(i) ABC is a right triangle provided n2 − m2 = r2.
(ii) Triangle with side lengths m + 2, n + 2 and r + 2 is a right-angle triangle.
(iii) Triangle with side lengths 2m, 2n and 2r is a right-angle triangle.
Which of these is correct? 
(a) Statement (i) would be correct if n > m, n > r and statement 2 would be correct if ABC is a right triangle.
(b) Statement (i) would be correct if r > m, r > n and statement 2 would be correct if ABC is a right triangle.
(c) Statement (i) would be correct if n > m, n > r and statement 3 would be correct if ABC is a right triangle.
(d) Statement (i) would be correct if r > m, r > n and statement 3 would be correct if ABC is a right triangle.

Question. In figure, ABC is an isosceles triangle, right-angled at C. Therefore

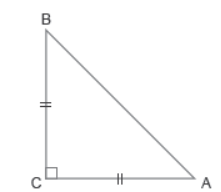
(a) AB² = 2AC²
(b) BC² = 2AB²
(c) AC² = 2AB²
(d) AB² = 4AC²

Question. In figure, ∠BAC = 90° and AD ⊥ BC. Then,
(a) BD . CD = BC²
(b) AB . AC = BC²
(c) BD . CD = AD²
(d) AB . AC = AD²

Question. If D, E and F are mid points of sides BC, CA and AB repspectively of DABC, then the ratio of the areas of triangles DEF and ABC is
(a) 2 : 3
(b) 1 : 4
(c) 1 : 2
(d) 4 : 5

Question. ABCD is a parallelogram with diagonal AC. If a line XZ is drawn such that XZ ; ; AB then XC BX is equal to
(a) AY/AC
(b) DZ/AC
(c) AZ/ZD
(d) AC/AY

Question. Sum of squares of the sides of rhombus is equal to
(a) Sum of diagonals
(b) Difference of diagonals
(c) Sum of squares of diagonals
(d) none of them

Question. From the given figure, then length of the sides AB and BD.

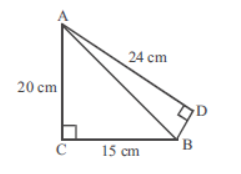
(a) 25 cm and 7 cm
(b) 25 cm and 17 cm
(c) 7 cm and 15 cm
(d) 18 cm and 7 cm

Question. The area of a right angled isosceles triangle whose hypotenuse is equal to 270 m is-
(a) 19000 m²
(b) 18225 m²
(c) 17256 m²
(d) 18325 m²

Question. The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, then AB =
(a) 10 cm
(b) 20 cm
(c) 25 cm
(d) 15 cm

Question. In ABC, AB/A=BD/DC, ∠B = 70° and ∠C = 50°. Then, ∠BAD = _______.

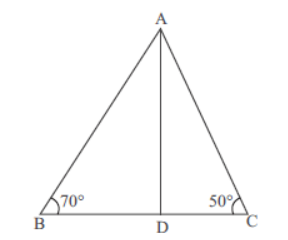
(a) 30°
(b) 40°
(c) 50°
(d) 45°

Question. In the given figure, DE || BC. The value of EC is

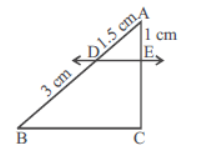
(a) 1.5 cm
(b) 3 cm
(c) 2 cm
(d) 1 cm

Question. Which of the following statement is false?
(a) All isosceles triangles are similar.
(b) All quadrilateral triangles are similar.
(c) All circles are similar.
(d) None of the above

Question. If ΔABC ~ ΔAPQ and ar (ΔAPQ) = 4 ar (ΔABC), then the ratio of BC to PQ is
(a) 2 : 1
(b) 1 : 2
(c) 1 : 4
(d) 4 : 1

Question. Consider a DPQR in which the relation QR² + PR² = 5 PQ² holds. Let G be the points of intersection of medians PM and QN. Then ∠QGM is always
(a) less than 45°
(b) obtuse
(c) a right angle
(d) acute and larger than 45°

Question. The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, then the length of QR is
(a) 4 cm
(b) 4.5 cm
(c) 3 cm
(d) 6 cm

Question. If ΔABC ~ ΔDEF such that BC = 2.1cm and EF = 2.8 cm. If the area of triangle DEF is 16 cm², then the area of triangle ABC (in sq. cm) is
(a) 9
(b) 12
(c) 8
(d) 13

Question. The length of the side of a square whose diagonal is 16 cm, is
(a) 8√ 2 cm
(b) 2√ 8 cm
(c) 4 √2 cm
(d) 2 √2 cm

Question. ΔABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Ratio between the areas of ΔABE and ΔACD is
(a) 1 : 4
(b) 2 : 1
(c) 1 : 2
(d) 4 : 3

Question. In the figure, ABC is a triangle in which AD bisects ∠A, AC = BC, ∠B = 72° and CD = 1cm. Length of BD (in cm) is

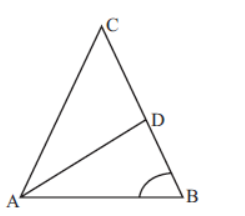
(a) 1
(b) 1 /2
(c) √5 –1 /2
(d) √3 + 1/2

Question. Two isosceles triangles have their corresponding angles equal and their areas are in the ratio 25 : 36. The ratio of their corresponding height is
(a) 25 : 35
(b) 36 : 25
(c) 5 : 6
(d) 6 : 5

Question. Let P be an interior point of a DABC. Let Q and R be the reflections of P in AB and AC, respectively. If Q, A, R are collinear, then ∠A equals
(a) 30°
(b) 60°
(c) 90°
(d) 120°

Question. The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Then

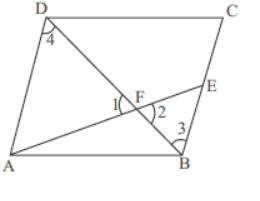
(a) EF/ FA= FB / AB 
(b) DF × EF = FB × FA
(c) DF × EF = (FB)²
(d) None of these

Question. ΔABC is an equilateral triangle with each side of length 2p. If AD ⊥ BC, then the value of AD is
(a) √3
(b) √3 p
(c) 2p
(d) 4p

Question. In a triangle ABC, ∠BAC = 90°; AD is the altitude from A on to BC. Draw DE perpendicular to AC and DF perpendicular to AB. Suppose AB = 15 and BC = 25. Then the length of EF is
(a) 12
(b) 10
(c) 5 √3
(d) 5√ 5

Question. The areas of two similar triangles are 81 cm2 and 49 cm2 respectively, then the ratio of their corresponding medians is
(a) 7 : 9
(b) 9 : 81
(c) 9 : 7
(d) 81 : 7

Question. If ΔABC is an equilateral triangle such that AD ⊥ BC, then AD² = A. 3a²/4 B. 3a²/2 C.3/4BC² D.√3/2^a 
(a) A and C
(b) A
(c) D
(d) B and C

Question. Let D be a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. If AC = 21 cm, then the side of an equilateral triangle whose area is equal to the area of the rectangle with sides BC and DC is
(a) 14 × 3^1/2
(b) 42 × 3^–1/2
(c) 14 × 3^3/4
(d) 42 × 3^1/2

Question. In a right angled triangle ΔABC, length of two sides are 8cm and 6cm, then which among the given statements is/ are correct?

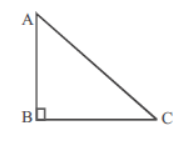
(a) Length of greatest side is 10cm
(b) ∠ACB = 45°
(c) ∠BAC = 45°
(d) Pythagoras theorem is not applicable here.

Question. Let ABC be a triangle and M be a point on side AC closer to vertex C than A. Let N be a point on side AB such that MN is parallel to BC and let P be a point on side BC such that MP is parallel to AB. If the area of the quadrilateral BNMP is equal to 5/18 of the area of DABC, then the ratio AM/MC equals
(a) 5
(b) 6
(c) 18/ 5
(d) 15/ 2

Question. Which among the following is/are correct?
(a) The ratios of the areas of two similar triangles is equal to the ratio of their corresponding sides.
(b) The areas of two similar triangles are in the ratio of the corresponding altitudes.
(c) The ratio of area of two similar triangles are in the ratio of the corresponding medians.
(d) If the areas of two similar triangles are equal, then the triangles are congruent.

Question. In ΔABC, AB = AC, P and Q are points on AC and AB respectively such that BC = BP = PQ = AQ. Then, ∠AQP is equal to (use p =180º)
(a) 2π /7 
(b) 3π/7
(c) 4π/7
(d) 5π/7

Fill in the Blanks :

Question. Two polygons of the same number of sides are similar, if all the corresponding angles are ………….

Question. All ……….. triangles are similar.

Question. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO= CO/ DO . ABCD is a ………….

Question. All congruent figures are similar but the similar figures need …………. be congruent.

Question. Two polygons of the same number of sides are similar, if their corresponding angles are ……… and their corresponding sides are in the same ………..

Question. A line drawn through the mid-point of one side of a triangle parallel to another side bisects the …………. side.

Question. If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the ………….. side.  

True or False :

Question. If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.

Question. If in two triangles, corresponding sides are in the same ratio, then their corresponding angles are equal and hence the triangles are similar. 

Question. Two figures having the same shape but not necessarily the same size are called similar figures.

Question. If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are similar. 

Match the Following :

Question . If in a Δ ABC, DE || BC and intersects AB in D and AC in E, then.

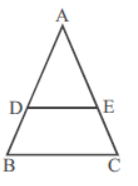
Column-I	Column-II
(A) AD/ DB	(p) AC/ AE
(B) AB /AD	(q) AE /EC
(C) DB /AB	(r) AE/ AC
(D) AD/ AB	(s) EC/ AC

Question . In figure, the line segment XY is parallel to the side AC of ΔABC and it divides the triangle into two parts of equal areas, then,

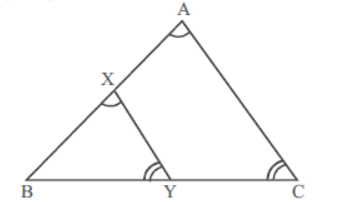
Column-I	Column-II
(A) AB : XB	(p) √2 :1
(B) ar (Δ ABC) : ar (Δ XBY)	(q) 2 : 1
(C) AX : AB	(r) (√2 −1)2 : √2
(D) ∠ X : ∠ A	(s) 1 : 1