Please refer to Mechanical Properties of Fluids Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Mechanical Properties of Fluids Notes and Questions
- Deforming force:- A force acting on a body which produces change in its shape of body instead of its state of rest or uniform motion of the body.
- Elasticity:-The property of matter by virtue which it regains its original shape and size, when the deforming forces are removed is called elasticity.
- Plasticity:- The inability of a body to return to its original shape and size, when the deforming forces are removed is called plasticity.
- Hooke’s law:- when a wire is loaded within elastic limit, the extension produced in wire is directly proportional to the load applied.
OR
Within elastic limit stress α strain
Stress = Constant
Strain - Stress :- Restoring force set up per unit area when deforming force acts on the body


Strain:- The ratio of change in dimension to the original dimension is called strain

Modulus of elasticity are of 3 types.
(1) Young’s Modulus (Y) = Normal stress /Longitudinal Strain
(2) Bulk Modulus (K) = Normal stress / Volumetric Strain
(3) Modulus of rigidity modulus (ƞ) = Tangetial stress / Shearing Strain
- Compressibility : the reciprocal of bulk modulus of a material is called its
compressibility
Compressibility = 1/K
Stress – Strain- diagram - Proportionality limit(P) – The stress at the limit of proportionality point P is known as proportionality limit
- Elastic limit – the maximum stress which can be applied to a wire so that on unloading it return to its original length is called the elastic limit
- Yield point(Y)- The stress, beyond which the length of the wire increase virtually for no increase in the stress
- Plastic region- the region of stress- strain graph between the elastic limit and the breaking point is called the plastic region.
- Fracture point or Breaking point(B)- the value of stress corresponding to which the wire breaks is called breaking point
- Work done in stretching a wire per unit volume/energy sored per unit volume of specimen = ½ x stress x strain
- Elastic after effect:- The delay in regaining the original state by a body after the removal of the deforming force is called elastic after effect.
- Elastic fatigue:- the loss in strength of a material caused due to repeated alternating strains to which the material is subjected.
- Poisson’s ratio(ϭ) :- The ratio of lateral strain to longitudinal strain is called Poisons ratio = Lateral Strain / Longitudinal Strain
- Relation between Y,K,¶, ϭ
1. Y=3K(1-2 ϭ)
2. Y=2¶(1+ ϭ)
3. ϭ =3k -2 ¶/2¶ + 6k
4. 3/y = 1/K +3/¶
- Applications of elasticity
1. Metallic part of machinery is never subjected to a stress beyond the elastic limit of material.
2. Metallic rope used in cranes to lift heavy weight are decided on the elastic limit of material
3. In designing beam to support load (in construction of roofs and bridges)
4. Preference of hollow shaft than solid shaft
5. Calculating the maximum height of a mountain
MECHANICS OF FLUID
Pressure :The force/threat acting per unit area is called pressure
S.I Unit of pressure is N/M2 or pascal (Pa)
Dimensional formula (ML-1T-2)
- Pascal’s law:- Pressure applied to an enclosed fluid is transmitted to all part of the fluid and to the wall of the container.
- Application of Pascal’s law:-
(1) Hydraulic lift, presses etc.
(2) Hydraulic brakes
- Pressure exerted by liquid column:- P = hρg, where h= depth of liquid, ρ=density , g=accn. due to gravity.
- Variation of pressure with depth: P = Pa + hρg, where Pa =atmospheric pressure
- Atmospheric pressure:- The pressure exerted by atmosphere is called atmospheric pressure.
At sea level, atmospheric pressure= 0.76m of Hg column
Mathematically 1 atm = 1.013 x 105 Nm-2
- Archimedes’ principle:- It states that when a body is immersed completely or partly in a fluid, it loses in weight equal to the weight of the fluid displaced by it.
Mathematically: Apparent weight = True weight – Vρg
Where V is volume of fluid displaced, ρ is its density.
- Viscosity:- It is the property of liquid (or gases) due to which a backward dragging force acts tangentially between two layers of liquid when there is relative motion between them.
- Newton’s formula for Viscous force:- the viscous force between two liquid layer each of area A and having a velocity gradient dv/dx is
F = ƞ A (dv/dx) , where ƞ is coefficient of viscosity
- Coefficient of viscosity:- It is define as the tangential viscous force which maintains a unit velocity gradient between two parallel layers each of unit area
S.I unit of coefficient of viscosity is poiseuille or pascal-second
- Poiseuille’s equation:- when a liquid of coefficient of viscosity flows through a tube of length ‘l’ and radius r, then the volume of liquid following out per second is given
V = πPr4/8 ƞl ,
Where P is the difference of pressure between the two ends of the tube.
- Stoke’s law: The backward dragging force acing on a small sphere of radius r falling with uniform velocity v through a medium of coefficient of viscosity is given by
F = 6π ƞrv
- Terminal velocity:- It is the maximum constant velocity acquired by the body while falling freely in a viscous medium The terminal velocity v of a spherical body of radius r and density ϭ while falling freely in a viscous medium of viscosity ¶ , density is given by
V = 2/q r2 /ƞ (6-p)g
- Stream line:- It is the path, straight or curved, the tangent at any point to which given the direction of the flow of liquid at that point
- Tube of flow:- A tube of flow is a bundle of stream lines having the same velocity of fluid elements over any cross section perpendicular to the direction of flow
- Stream line flow:- the flow of the liquid in which each molecule of the liquid passing through a point travels along the same path and with the some velocity as the preceeding molecule passing through the same point
- Laminar flow:- the flow of liquid, in which velocity of the layer varies from maximum at the axis to minimum for the layer in contact with the wall of the tube is called laminar flow.
- Turbulent flow:- It is the flow of liquid in which a liquid moves with a velocity greater than its critical velocity. The motion of the particles of liquid becomes disorderly or irregular.
- Critical velocity:- It is that velocity of liquid flow, upto which the flow of liquid is streamlined and above which its flow becomes turbulent. Critical velocity of a liquid (Vc) flowing through a tube is given by
Vc = Kƞ/ ρ r
Where ρ is the density of liquid following through a tube of radius r and ƞ the coefficient of viscosity of liquid
- Reynold’s umber:- It is a pure number which determines the nature of flow of liquid through a pipe Quantitatiively Renold’s number N = ρ D Vc/ ƞ
Where ƞ is coefficient of viscosity of liquid , ρ is density of liquid D is
the diameter of the tube, Vc is critical velocity
For stream line flow, Reynold’s number <2000
For turbulent flow, Reynold’s number > 3000
For uncertain flow, 2000<Reynold’s number<3000
- Theorem of continuity : If there is no source or sink of the fluid along the length of the pipe, the mass of the fluid crossing any section of the pipe per second is always constant
Mathematically a1v1 ρ 1 = a2v2 ρ2
It is called the equation of continuity
For in compressible liquid ρ 1= ρ 2 Therefore the equation continuity becomes
a1v1 =a2v2
Bernoulli’s theorem:- It states that for an in compressible non-viscous liquid in steady flow, the total energy i.e. pressure energy, potential energy and kinetic energy remains constant its flow.
Mathematically p/q + gh + 1/2 V2 = Constant
p/pg +h + v2/2g = Constant
The term p/pg , h and v2/2g are called pressure head, gravitational head and velocity head respectively.
- Application of Bernoull’s theorem
(i) Working of Bunsen burner
(ii) Lift of an air foil
(iii) Spinning of ball (Magnus effect)
(iv) Sprayer
(v) Ping pong ball in air jet.
- Toricelli’s theorem/speed of efflux:- It states that the velocity of efflux i.e. the velocity with which the liquid flows out of an orifice (i.e. a narrow hole) is equal to that which is freely falling body would acquire in falling through a vertical distance equal to the depth of orifice below the free surface of liquid.
Quantitatively velocity of efflus
V = √2gh
Venturimeter:- It is a device use to measure the rate of flow of liquid. Venturimeter consists of a wide tube having a constriction in the middle. If a1 and a2 are the areas of cross section of the wide end and the threat, p1 and p2
are the pressure of liquid, then velocity of the liquid entering at the wide end is given by V1=a2 √ 2(P1-P2) ρ(a12-a22)
- Surface tension (T) :- It is the property of a liquid by virtue of which, it behaves like an elastic stretched membrane with a tendency to contract so as to occupy a minimum surface area Mathematically T = F/l
S.I Unit is : Nm-1 Dimensional formula : ML0T -2
Surface Energy : The potential energy per unit area of the surface film is called the surface energy.
Surface energy = Work done in increasing the surface area /Increase in area
Surface tension is numerally equal to surface energy
Excess of pressure inside a drop and double:- There is excess of pressure on concave side of a curved surface
1. Excess of pressure inside a liquid drop = 2T/R
2. Excess of pressure inside a liquid bubble = 4T/R
3. Excess of pressure inside an air bubble = 2T/R, Where T is the surface tension , R = radius of liquid drop
- Angle of contact:- The angle which the tangent to the free surface of the liquid at the point of contact makes with the wall of the containing vessel, is called the angle of contact
For liquid having convex meniscus, the angle of contact is obtuse and for having concave meniscus, the angle of contact is acute. - Capillary tube:- A tube of very fine bore is called capillary tube
- Capillarity:-The rise or fall of liquid inside a capillary tube when it is dipped in it is called capillarity
- Ascent formula:- when a capillary tube of radius ‘r’ is dipped in a liquid of density s and surface tension T, the liquid rises or depresses through a height, H= 2Tcosθ /r ρ g
- There will be rise a liquid when angle of contact θ is acute. There will be fall in liquid when angle of contact θ is obtuse.
Thermal expansion and calorimetry
- Heat- it is a form of energy, which produce in us the sensation of warmth
- Temperature:- The degree of hotness or coldness of a body is called temperature
- Thermometer- It is a device used to measure the temperature of a body
- Scales of temperature:- there are four scales of temperature. Given below is scales of temp with lower and upper fixed point
- Temperature scales Lower fixed point (Melting point office) Upper fixed point (Boiling point of water)
1. Celsius 00C 1000C
2. Fahrenheit 320F 2120F
3. Reamur 00R 80oR
4. Kelvin 273K 373K
- Relation between the various temperature scales
If C,F, R and K are temperature of a body on Celsius, Fahrenheit , Reumer and Kelvin scale, then
C/5 = F-32/9 = R/4 = K -273 /5 - Thermal expansion:- all solid expands on heating. There are three types of expansion.
(1) Liner expansion- When a solid rod of initial length ‘l’ is heated through a temperature ΔT then its new length l’ = l( 1+α ΔT) , where α is called coefficient of liner expansion
(2) Superficial expansion- when a solid of initial surface area A is heated through temperature then its new Area is A’= A (1 + β ΔT ), where β is coefficient of superficial expansion
(3) Cubical expansion- when a solid of initial volume V is heated through a temperature ΔT then its new volume is V’= V ( 1 + ΔT ) ,where ϒ is the coefficient of cubical expansion.
- Relation between α ,β and ϒ
α= β/2 =ϒ/3 - In case of liquid ϒr= ϒa+ ϒg
Where ϒr=Coefficient of real expansion of a liquid
ϒa= Coefficient of apparent expansion of liquid
ϒg= Coefficient of cubical expansion of the vessel - Thermal capacity = It is the amount of heat required to raise its temperature through one degree
- Water equivalent :- It is the mass of water which absorbs or emits the same amount of heat as is done by the body for the same rise or fall in temperature. It is represented by W = mc
- Specific heat :- It is the amount of heat required to raise the temperature of unit mass of substance through unit degree Celsius
C = ΔQ /mΔT
- Latent heat :- It is define as the quantity of heat required to change the unit mass of the substance from its one state completely to another state at constant temperature

- Mathematically Q = ML
- Calorimeter :- Device used for measuring heat
- Principle of calorimetry :- Heat loss by hot body = Heat gain by cold body
- Transfer of heat :- there are three modes by which heat transfer takes place
(1) Conduction:- It is the process by which heat is transmitted from one point to another through a substance in the direction of fall of temperature without the actual motion of the particles of the substance.
When two opposite faces of a slab, each of cross section A and separated by a distance d are maintained at temperature T1 and T2 (T1 >T2), then amount of heat that flows in time t
Q =K A (T1 –T2)t/d Where K is coefficient of thermal conductivity of the mater
Coefficient of thermal conductivity:- It may be defined as the quantity of heat energy that flows in unit time between the opposite faces of a cube of unit side, the faces being kept at one degree difference of temperature S.I unit of coefficient of thermal conductivity : J S-1m-1K-1 or W m-1K-1
(2) Convection:- It is the process by which heat is transmitted through a substance from one point to another due to the bodily motion of the heated particles of the substance.
(3) Radiation:- It is the process by which heat is transmitted from one place to another without heating the intervening medium
- Newton’s laws of cooling:- It states that the rate of loss of heat or rate of cooling of a body is directly proportional to the temperature difference between the body and the surrounding, provided the temperature difference is
small
Mathematically -dQ/dt = K(T-T0)
- Perfect black body:- It is a body which absorbs heat radiations of all the wavelengths, which fall on it and emits the full radiation spectrum on being heated.
- Stefan’s law:- It states that the total amount of heat energy radiated per unit area of a perfect black body is directly proportional to the fourth power of the absolute temperature of the substance of the body Mathematically E α T4
E = Σ T4 Where is called Stefan’s constant
It’s value is 5.67 x 10-8 JS-1m-2k-4
Wein’s displacement law:- According to this law, the wavelength λm of maximum intensity of emission of black body radiation is inversel y proportional to absolute temperature (T) of black body.
λm α 1/T
λm T = b where b is wien’s constant
Question and Answer :
Question. The Young’s modulus of steel is much more than that for rubber. For the same longitudinal strain, which one will have greater stress?
Answer. Stress= Y X longitudinal strain. So steel will have greater stress.
Question. Which of the two forces – deforming or restoring is responsible for elastic behavior of substance?
Answer. Restoring force.
Question. Which mode of transfer of heat is the quickest?
Answer. Radiation.
Question. A boat carrying a number of large stones is floating in a water tank. What will happen to the level of water if the stones are unloaded into the water?
Answer. The level of water will fall because the volume of the water displaced by stones in water will be less than the volume of water displaced when stones are in the boat.
Question. A rain drop of radius r falls in air with a terminal velocity v. What is the terminal velocity of a rain drop of radius 3r ?
Answer.

Question. When air is blown in between two balls suspended close to each other , they are attracted towards each other. Why?
Answer. On blowing air between the two balls, the air velocity increases, decreasing pressure. The pressure on the outer side of the ball being more will exert forces on the balls, so they move towards each other.
Question. A wire is stretched by a force such that its length becomes double. How will the Young’s modulus of the wire be affected?
Answer. Young’s modulus remains the same.
Question. How does the Young’s modulus change with rise in temperature?
Answer. Young’s modulus of a material decreases with rise in temperature.
Question. Which of the three modulus of elasticity – Y, K and η is possible in all the three states of matter (solid, liquid and gas)?
Answer. Bulk modulus (K)
Question. Why does air bubble in water goes up?
Answer. The terminal velocity , V = 2r2(ς – σ)g/9η As the density of air ς is less than density of water , the terminal velocity is negative. For this reason air bubbles moves upward.
Question. Steel is more elastic than rubber. Explain.
Answer. Consider two wire, one of steel and another of rubber having equal length L and cross sectional area A . When subjected to same deforming force F, the extension produce in steel is lS and in rubber is lR such that lR>lS.

Hence steel is more elastic.
Question. The pressure of a medium is changed from 1.01 X 1o5 pa to 1.165 X 105 pa and changed in volume is 10% keeping temperature constant. Find the bulk modulus of the medium.
Answer. Here Δp = 1.165 X 105 – 1.01 X 105 = 0.155 X 105 pa
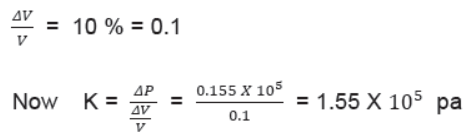
Question. identical drops of water are falling down vertically in air each with a terminal velocity of 0.15m/s. If they combine to form a single bigger drop, what will be its terminal velocity?
Answer. Let r = radius of each drop, v = 0.15 m/s

Volume of big drop = Volume of 27 small drops

Let R be the radius of the big drop.
Let v1 be the terminal velocity of bigger drop


v1 = 9v = 9 X 0.15 = 1.35 m/s
Question. Water flows through a horizontal pipe line of varying cross section at the rate of 0.2m3s-1. Calculate the velocity of water at a point where the area of cross section of the pipe is 0.02m2.
Answer. Rate of flow = av

Question. A cylinder of height 20m is completely filled with water. Find the efflux water (in m s-1) through a small hole on the side wall of the cylinder near its bottom. Given g = 10m/s.
Answer. Here h = 20m , g = 10 m/s
Velocity of efflux , v = √2gh = √2x10x20 = 20m/s
Question. At what common temperature would a block of wood and a block of metal appear equally cold or equally hot when touched?
Answer. When touched an object appear cold if heat flows from our hand to the object. On the other hand it appears hot, if heat flows from the object towards our hand. Therefore a block of wood and block of metal will appear equally cold or equally hot if there is no exchange of heat between hand and the block. So the two blocks will appear equally cold or equally hot if they are at the same temperature as that of our hands i.e. the temperature of our body.
Question. A wire stretches by a certain amount under a load. If the load and radius are both increased to four times, find the stretch caused in the wire.
Answer. For a wire of radius r stretched under a force F,
Y =FL/ πr2L Or l = FL/πr2Y
Let l’ be the extension when both the load and the radius are increased to four times,
Then, l’ = 4 FXL /π(4r)2L = FL/π4r2Y l/4
Question. A slab of stone of area 0.36m2 and thickness of 0.1m is exposed to the lower surface of steam at 100 . A block of ice at 0°C rest on the upper surface of the slab. In one hour 4.8 Kg of ice is melted. Calculate the thermal conductivity of stone.
Answer. Here A = 0.36m2 , d = 0.1m , T1 – T2 = 100 – 0 = 100°C t = 1hr = 3600 sec
Mass of ice melted M = 4.8 Kg
We know Latent heat of ice L = 336 X 103 J Kg-1
Heat required to melt the ice Q = ML = 4.8 X 336 X103 = 1.613 X 106 K

Question. Calculate the percentage increase in the length of a wire of diameter 2mm stretched by a force of 1kg F. Young’s modulus of the material of wire is 15 X 1010Nm-2. 13
Answer. F = 1 Kg F = 9.8N Y = 15 X 1010Nm-2 r =2/2= 1mm = 10-3m
Cross section of wire , πr2 = π X (10-3)2 = π X 10-6m2

Question. A piece of chalk immersed into water emits bubbles in all directions. Why?
Answer. A piece of chalk has extremely narrow capillaries. As it is immersed in water, water rises due to capillary action. The air present in the capillaries in the chalk is forced out by the rising water. As a result bubbles are emitted from the chalk in all the directions.
Question. Water at a pressure of 4 X 104 Nm-2 flows at 2ms-1 through a pipe of 0.02m2 cross sectional area which reduces to 0.01m2. What is the pressure in the smaller cross section of the pipe?
Answer. a1v1 = a2v2
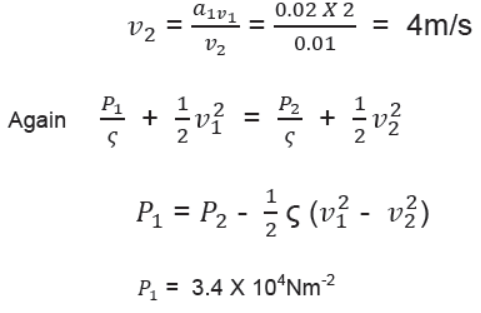
Question. Calculate the energy spent in spraying a drop of mercury of 1 cm radius into 106 droplets all of same size. Surface tension of mercury is 35 x 10-3 Nm-1.
Answer. T = 35 x 10-3 Nm-1 R = 1 cm
Let r be the radius of each small drop, when the original drop is spitted into 106 small drops.
Then 106 X 4/3 πr3 = 4/3 π R3
r = 10-2 R
r = 10-2 X 1 = 10-2 cm
Initial surface area of the original drop = 4π R2 = 4π X 12 = 4π cm2
Final surface area of the 106 small drops = 106 X 4πr2 = 106 X 4π X ( 10-2)2 = 400π cm2
Therefore increase in surface area = 400π – 4π = 396 cm2 = 396π X 10-4m2
Therefore energy spent = T X increase in surface area = 35 X 10-3 X 396π X 10-4 = 4.354 X 10-3N
Question. A liquid takes 10 minutes to cool from 70°C to 50°C . How much time will it take to cool from 60°C to 40°C ? The temperature of the surrounding is 20°C .
Answer.

Question. A piece of iron of mass 0.1 kg is kept inside a furnace, till it attains the temperature of the furnace. The hot piece of iron is dropped into a calorimeter containing 0.24 Kg of water at 20 . The mixture attains an equilibrium temperature of 60 . Find the temperature of the furnace. Given water equivalent of calorimeter = 0.01 kg and specific heat of iron
= 470 J Kg-1 K-1.
Answer. Let θ1 be the temperature of the furnace i.e of the piece of iron.
Heat lost by the piece of iron Q = M1C1 (θ1 – θ)
Here M1 = 0.1 Kg C1 = 470 J Kg-1 K-1 θ = 60°
Q = 0.1 X 470 (θ1 – 60 θ ) = 47 (θ1 – 60 ) ————————- (1)
Heat gain by water and the calorimeter , Q = (M2 + w) C2 (θ – θ2 )
M2 = 0.24 Kg w = 0.01 Kg = θ220°C C2 = Specific heat of water = 4200 J Kg-1 K-1
Q = (0.24 + 0.01) x 4200 X (60 – 20) = 42000 ————————-(2)
From (1) and (2) 47 (θ1 – 60 ) = 42000
θ1 = 953.62°C
Viscosity
The property of a fluid by virtue of which an internal frictional force acts between its different layers which opposes their relative motion is called viscosity.
These internal frictional force is called viscous force.
Viscous forces are intermolecular forces acting between the molecules of different layers of liquid moving with different velocities.

where, (dv/dx) = rate of change of velocity with distance called velocity gradient, A = area of
cross-section and = coefficient of viscosity.
SI unit of η is Nsm-2 or pascal-second or decapoise. Its dimensional formula is [ML-1T-1].
The knowledge of the coefficient of viscosity of different oils and its variation with
temperature helps us to select a suitable lubricant for a given machine.
Viscosity is due to transport of momentum. The value of viscosity (and compressibility) for ideal liquid is zero.
The viscosity of air and of some liquids is utilised for damping the n.ving parts of some instruments.
The knowledge of viscosity of some organic liquids is used in determining the molecular weight and shape of large organic moleculars like proteins and cellulose.
Variation of Viscosity
The viscosity of liquids decreases with increase in temperature

where, η0 and ηt is are coefficient of viscosities at 0°C t°C, α and β are constants.
The viscosity of gases increases with increase in temperatures as
η ∝ √T
The viscosity of liquids increases with increase in pressure but the viscosity of water decreases with increase in pressure.
The viscosity of gases do not changes with pressure.
Poiseuille’s Formula
The rate of flow (v) of liquid through a horizontal pipe for steady flow is given by

where, p = pressure difference across the two ends of the tube. r = radius of the tube, n = coefficient of viscosity and 1 = length of th tube.
The Rate of Flow of Liquid
Rate of flow of liquid through a tube is given by
v = (P/R)
where, R = (8 ηl/πr4), called liquid resistance and p = liquid pressure.
(i) When two tubes are connected in series
- Resultant pressure difference p = p1 + p2
- Rate of flow of liquid (v) is same through both tubes.
- Equivalent liquid resistance, R = R1 + R2
(ii) When two tubes are connected in parallel
1. Pressure difference (p) is same across both tubes.
2. Rate of flow of liquid v = v1 + v2
3. Equivalent liquid resistance (1/R) = (1/R1) + (1/R2)
Stoke’s Law
When a small spherical body falls in a long liquid column, then after sometime it falls with a constant velocity, called terminal velocity. When a small spherical body falls in a liquid column with terminal velocity then viscous force acting on it is
F = 6πηrv
where, r = radius of the body, V = terminal velocity and η = coefficient of viscosity.
This is called Stoke’s law.
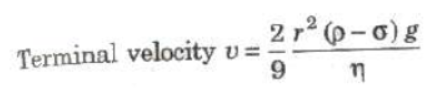
where,
- ρ = density of body,
- σ = density of liquid,
- η = coefficient of viscosity of liquid and,
- g = acceleration due to gravity
1. If ρ > ρ0, the body falls downwards.
2. If ρ < ρ0, the body moves upwards with the constant velocity.
3. If po << ρ, v = (2r2ρg/9η)
Importance of Stoke’s Law
1. This law is used in the determination of electronic charge by Millikan in his oil drop experiment.
2. This law helps a man coming down with the help of parachute.
3. This law account for the formation of clouds.
Flow of Liquid
1. Streamline Flow The flow of liquid in which each of its particle follows the same path as followed by the proceeding particles, is called streamline flow.
2. Laminar Flow The steady flow of liquid over a horizontal surface in the form of layers
of different velocities, is called laminar flow.
3. Turbulent Flow The flow of liquid with a velocity greater than its critical velocity is disordered and called turbulent flow.
Critical Velocity
- The critical velocity is that velocity of liquid flow, below which its fl is streamlined and above
- which it becomes turbulent.
- Critical velocity vc = (kη/rρ)
- where,
- K = Reynold’s number,
- η = coefficient of viscosity of liquid r = radius of capillary tube and ρ = density of the liquid.
Reynold’s Number
Reynold’s number is a pure number and it is equal to the ratio of inertial force per unit area to the viscous force per unit area for flowing fluid.
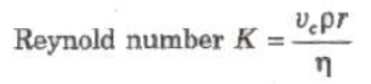
where, p = density of the liquid and vc = critical velocity.
For pure water flowing in a cylindrical pipe, K is about 1000.
When 0< K< 2000, the flow of liquid is streamlined.
When 2000 < K < 3000, the flow of liquid is variable betw streamlined and turbulent.
When K > 3000, the flow of liquid is turbulent.
It has no unit and dimension.
Equation of Continuity
If a liquid is flowing in streamline flow in a pipe of non-unif cross-section area, then rate of flow of liquid across any cross-sec remains constant.
a1v1 = a2v2 av = constant
The velocity of liquid is slower where area of cross-section is larger faster where area of crosssection is smaller.

The falling stream of water becomes narrower, as the velocity of f stream of water increases and therefore its area of cross-s decreases.
Energy of a Liquid
A liquid in motion possess three types of energy
(i) Pressure Energy Pressure energy per unit mass = p/ρ
where,
p= pressure of the liquid and p = density of the liquid.
Pressure energy per unit volume = p
(ii) Kinetic Energy
- Kinetic energy per unit mass = (1/2v2)
- Kinetic energy per unit volume = 1/2ρv2
(iii) Potential Energy
- Potential energy per unit mass = gh
- Potential energy per unit volume = ρgh
Bernoulli’s Theorem
If an ideal liquid is flowing in streamlined flow then total energy, i.e., sum of pressure energy, kinetic energy and potential energy per unit
volume of the liquid remains constant at every cross-section of the tube.
Mathematically

It can be expressed as

where, (p/ρg) = pressure head, (v2/2g) = velocity head and h = gravitational head.
For horizontal flow of liquid,

- where, pis called static pressure and (1/2 ρv2) is called dynamic pressure.
- The erefore in horizontal flow of liquid, if p increases, v decreases and Nce-versa.
- The theorem is applicable to ideal liquid, i.e., a liquid which is non-viscous incompressible and irrotational.
Applications of Bernoulli’s Theorem
1. The action of carburetor, paintgun, scent sprayer atomiser insect sprayer is based on Bernoulli’s theorem.
2. The action of Bunsen’s burner, gas burner, oil stove exhaust pump is also based on Bernoulli’s theorem.
3. Motion of a spinning ball (Magnus effect) is based on Bernoulli theorem.
4. Blowing of roofs by wind storms, attraction between two close parallel moving boats, fluttering of a flag etc are also based Bernoulli’s theorem.
Venturimeter
It is a device used for measuring the rate of flow of liquid t pipes. Its working is based on Bernoulli’s theorem.
Rate of flow of liquid,
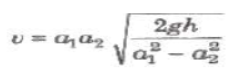

where, a1 and a2 are area of cross-sections of tube at bra and narrower part and h is difference of liquid columns in ver tubes.
Torricelli’s Theorem
Velocity of efflux (the velocity with which the liquid flows out orifice or narrow hole) is equal to the velocity acquired by a falling body through the same vertical distance equal to the dep orifice below the free surface of liquid.

Velocity of efflux, v = √2gh
where, h = depth of orifice below the free surface of liquid.
Horizontal range, S = √4h(H — h)
where, H = height of liquid column.
Horizontal range is maximum, equal to height of the liquid column H, when orifice is at half of the height of liquid column.
Important Points
- In a pipe the inner layer .central layer) have maximum velocity and the layer in contact with pipe have least velocity.
- Velocity profile of liquid flow in a pipe is parabolic.
- Solid friction is independent of area of surfaces in contact while viscous force depends on area of liquid layers.
- A lubricant is chosen ac:ording to the nature of machinary. In heavy machines lubricating oils of high viscosity are used and in light machines low viscosity oils are used.
- The cause of viscosity 1 liquids is the cohesive forces among their molecules while cause of viscosity in gases is diffusion.

We hope the above Mechanical Properties of Fluids Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


