Permutations and Combinations Class 11 Mathematics Important Questions

Students can read the important questions given below for Permutations and Combinations Class 11 Mathematics. Permutations and Combinations Class 11 Mathematics Important Questions Class 11 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 11 Mathematics Important Questions provided for all chapters to get better marks in examinations. Class 11 Mathematics Question Bank Class 11 is available on our website for free download in PDF.

Important Questions Permutations and Combinations Class 11 Mathematics

Question. How many positive numbers can be formed by using any number of the digits 0, 1, 2, 3 and 4; no digit being repeated in any number?
Answer : 260

Question. How many different numbers can be formed by using all the digits 1, 2, 3, 4, 3, 2, 1, so that odd digits always occupy odd places?
Answer : 18

Question. How many odd numbers less than 1000 can be formed using the digits 0, 1, 4 and 7 if repetition of digits is allowed?
Answer : 32

Question. In how many ways can five people be seated in a car with two people in the front seat and three in the rear, if two particular persons out of the five cannot drive?
Answer : 72

Question. How many even numbers of four digits can be formed with the digits 0, 1, 2, 3, 4, 5 and 6; no digit being used more than once?
Answer : 420

Question. How many even numbers are there with three digits such that if 5 is one of the digits in a number then 7 is the next digit in that number.
Answer : 365

Question. How many non-zero numbers can be formed using the digits 0, 1, 2, 3, 4 and 5 if repetition of digits is not allowed?
Answer : 1630

Question. In how many ways can 16 rupees and 12 paise coins be arranged in a line so that no two paise coins may occupy consecutive positions?
Answer : ¹⁷C₁₂ = 6188 when all rupee coins are identical and all paise coins are identical; 16! × ¹⁷C₁₂ , if coins of same value are different.

Question. 3 women and 5 men are to sit in a row for a dinner. Find in how many ways they can be arranged so that no two women sit next to each other.
Answer : 16! × 6C₃

Question. The letters of the word OUGHT are written in all possible orders and these words are written out as in a dictionary. Find the rank of the word TOUGH in this dictionary.
Answer : 89th

Question. If the difference permutations of all the letters of the word EXAMINATION are listed as in a dictionary, how many items are there in this list before the first word starting with E?
Answer : 907200

Question. In how many ways can 5 flags, in which 3 are red, one is white and one is blue, be arranged on a staff, one below the other, if flags of one colour are not distinguishable?
Answer : 20

Question. A biologist studying the genetic code is interested to know the number of possible arrangements of 12 molecules in a chain. The chain contains 4 different molecules represented by the initials A (for Adenine), C (for Cytosine), G (for Guanine) and T(for Thymine) and 3 molecules of each kind. How many different such arrangements are possible in all?
Answer : 369600

Question. In how many ways can 10 examination papers be arranged so that the best and the worst papers never come together.
Answer : 8.9 !

Question. A class consists of 40 girls and 60 boys. In how many ways can a president, vice president, treasure and secretary be chosen if the treasure must be a girl, the secretary must be a boy and a student may not hold more than one office?
Answer : 22814400

Question. Ali has 2 school bags, 3 tiffin boxes and 2 water bottles. In how many ways can he carry these items choosing one each.
Answer : 12

Question. Find n, if ^n-1P₃ : ⁿP₄ = 1 : 9 .
Answer : n = 9

Question. Find the total number of ways in which n distinct objects can be put into two different boxes so that no box remains empty.
Answer : 2ⁿ–2

Question. There are 3 nominations for the post of president, 4 for the post of vice-president and 5 for the secretary.
(i) In how many ways can candidates be selected for each of these posts ?
(ii) In how many ways can any one of these posts be filled ?
Answer : (i) 60 (ii) 12

Question. How many 3-digit numbers have exactly one of their digits as 5?
Answer : 225

Question. In how many ways can 3 people be seated in a row containing 7 seats?
Answer : 210

Question. Number 1, 2 and 3 are written on three cards. How many two digit numbers can be formed by placing two cards side by side ?
Answer : 6

Question. Find the number of numbers of 4 digits greater than 3000 that can be formed with the digits 0, 1, 2, 3, 4 and ‘5 if repetition of digits is allowed.
Answer : 647

Question. In a town, the car plate numbers contain only three or four digits, not containing the digit 0. What is the maximum number of cars that can be numbered?
Answer : 9³ + 9⁴ = 7290

Question. A person wants to go to another city by bus and return by train. He has a choice of 5 different buses and 4 trains to return. In how many ways can be perform his journey?
Answer : 20

Question. Eight children are standing in a queue.
(i) In how many ways can the queue be formed ?
(ii) How many arrangements are possible if the tallest child stands at the end of the queue ?
Answer : (i) 40320 (ii) 5040

Question. (i) Find the sum of all the four digit numbers which can be formed with the digits 0, 1, 2, and 3.
(ii) Find the sum of all the 4 digit numbers which can be fomed with the digits 1, 2, 2 and 3.
Answer : (i) 38664 (ii) 26664

Question. A gentleman has 6 friends to invite. In how many ways can he send invitation cards to them if he has three servants to carry the cards.
Answer : 729

Question. In how many ways can a student answer a set of ten true/false type question ?
Answer : 1024

Question. A teacher has to select either a boy or a girl from a class of 12 boys and 15 girls for coordinating a school function. In how many ways can she do it?
Answer : 27

Question. There are 5 routes from A to B and 3 routes from place B to place C. Find how many different routes are there from A to C via B.
Answer : 15

Question. How many numbers are there between 100 and 1000 in which all the digits are distinct ?
Answer : 648

Question. There are seven flags of different colours. A signal is generated using two flags How many different signals can be generated ?
Answer : 42

Question. There are 6 multiple choice questions in an examination. How many sequence of answers are possible, if the first three questions have 4 choices each and the next three have 5 each ?
Answer : 8000

Question. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Answer : 33810

Question. In how many ways 4 boys and 4 girls can be seated in a row so that boys and girls are alternate?
Answer : 1152

Question. In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate?
Answer : 144

Question. How many signals can be made by hoisting 2 blue, 2 red and 5 yellow flags on a pole at the same time?
Answer : 9! / 2! 2!5!

Question. How many different signals can be made by hoisting 6 differently coloured flags one above the other when any number of them may be hoisted at once?
Answer : ⁶P₁ + ⁶P₂ + ⁶P₃ + ⁶P₄ + ⁶P₅ + ⁶P₆ + 1956

Question. In how many ways 10 Indians, 5 Amercians and 4 Englishmen can be seated in a row so that neither Americans nor Englishmen sit between Indians.
Answer : 10! 10!

Question. In a dinner party there are 10 Indians, 5 Amercians and 5 Englishmen. In how many ways can they be seated in a row so that all persons of the same nationality sit together?
Answer : 3 ! 10! 5! 5!

Question. How many ways can the letters of the word ‘VIOLENT’ be arranged so that vowels occupy only the odd places ?
Answer : 576

Question. In how many different ways can the letters of the word ‘SALOON’ be arranged if the consonants and vowels must occupy alternate places?
Answer : 36

Question. In a class of students, there are 4 girls and 6 boys. In how many ways can they be seated in a row so that all the four girls are not together.
Answer : 10! – 7! 4!

Question. Six papers are set in an examination, 2 of them in Mathematics. In how many different orders can the papers be given if two Mathematics papers are not successive?
Answer : 6! – 5! 2!

Question. A number lock on a suitcase has 3 wheels each labelled with ten digits from 0 to 9. If opening of the lock is a particular sequence of three digits with no repeats, how many such sequences will be possible?
Answer : 720

Question. You are given 6 balls of different colours (black, white, red, green, violet, yellow), in how many ways can your arrange them in a row so that black and white balls may never come together?
Answer : 480

Question. (i) Find the number of words formed, with the letters of the word ‘DELHI’ when any letter may be repeated any number of times.
(ii) Find the number of 4 letter words, with or without meaning, which can be formed out of the letters of the word ‘ROSE’ where
(a) the repetition of the letters is not allowed.
(b) repetition of the letters is allowed.
Answer : (i) 5⁵ = 3125 (ii) (a) 24 (b) 256

Question. How many words can be formed by using the letters of the word ‘BHARAT’ ? How many of these words will not contain B and H together? How many of these start with B and end with T?
Answer : 360; 240; 12

Question. In how many ways can 4 boys and 3 girls be seated in a row so that no two girls are together?
Answer : 1440

Question. In how many ways can 15 I.Sc and 12 B.Sc. candidates be arranged in a line so that no two B.Sc candidates may occupy consecutive positions?
Answer : 15! × ¹⁶P

Question. How many different words can be formed with the letters of the word ‘VICE-CHANCELLOR’ so that the vowels are together ?
Answer : 5 × 10 !

Question. How many words ( with or without dictionary meaning) can be made from the letters in the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time ?
(ii) all letters are used at a time ?
(iii) all letters are used but the first letter is a vowel ?
Answer : (i) 360 (ii) 720 (iii) 240

Question. In how many ways can 18 white and 19 black balls be arranged in a row so that no two white balls may be together ? It is given that balls of the same colour are identical.
Answer : 190

Question. A customer forgets a four-digit code for an Automatic Teller Machine (ATM) in a bank. However, he remembers that this code consists of digits 3, 5, 6 and 9. Find the largest possible number of trials necessary to obtain the correct code.
Answer : 24

Question. There are 6 items in column A and 6 items in column B. A student is asked to match each item in column A with an item in column B. How many possible answers (correct or incorrect) are there to the question?
Answer : 720

Question. In how many distinct ways can the product xy2z2 be written without using exponents?
Answer : 30

Question. There are two books each of three volumes and two books each of two volumes. In how many ways can the ten books be arranged on a table so that the volumes of the same book are not separated.
Answer : 4 ! 3 ! 2 ! 2!

Question. A library has 5 copies of one book, 4 copies of each of 2 books, 6 copies of each of 3 books and single copies of 8 books. In how many ways can all books be arranged so that copies of the same book are always together?
Answer : 14

Question. There are 3 white, 4 red and 1 blue marbles in a bag. There are drawn one by one and arranged in a row. Assuming that all the 8 marbles are drawn, determine the number of different arrangements if marbles of same colour are indistinguishable.
Answer : 280

Question. Find the number of permutations of the letters of the word PRE-UNIVERSITY.
Answer : 19958392

Question. In how many ways can the letters of the word ‘CIVILIZATION’ be rearranged?
Answer : 13! / 2!2!2!

Question. How many different words can be formed with the letters of the word ‘UNIVERSITY’ so that all the vowels are together.
Answer : 60480

Question. In how many ways can 8 Indians, 4 Americans and 4 Englishmen be seated in a row so that all persons of the same nationality sit together.
Answer : 3 ! 8 ! 4 ! 4!

Question. There are 20 books of which 4 are single volume and the other are books of 8, 5 and 3 volumes respectively. In how many ways can all these books be arranged on a shelf so that volumes of the same book are not separated.
Answer : 7 ! 8 ! 5 ! 3!;

Question. In how many ways can the letters of the word ‘DIRECTOR’ be arranged so that the three vowels are never together?
Answer : 18000

Question. There are 6 candidates contesting for a certain office in a municipal election. In how many ways can their names be listed on a ballot paper ?
Answer : 720

Question. Find the number of rearrangements of the letters of the word ‘BENEVOLENT’. How many of them end in L?
Answer : 302399; 30240

Question. How many different words can be formed with the letters of the worked ‘PENCIL’ when vowels occupy even places.
Answer : 144

Question. How many different words can be formed with five given letters of which three are vowels and two are consonants, no two vowels being together in any word?
Answer : 12

Question. How many three digit numbers with distinct digits are there whose all the digits are odd?
Answer : 60

Question. (a) Find the number of possible outcomes of tossing a coin four times.
(b) (i) A class consists of 27 boys and 14 girls. In how many ways can one boy and one girl be selected to represent the class at a function ?
(ii) From a committee of 8 persons, in how many ways can we choose a chairman and a vice-chairman assuming that one person cannot hold more than one position.
Answer : (a) 16 (b) (i) 378 (ii) 56

Question. How many 4-digit numbers greater than 2300 can be formed with the digit 0, 1, 2, 3, 4, 5 and 6, no digit being repeated in any number?
Answer : 560

Question. A number of four different digits without repetition is formed by using the digits 1, 2, 3, 4, 5, 6, 7 Find
(i) How many such numbers can be formed?
(ii) How many of them are greater than 3400 ?
Answer : (i) 840 (ii) 560

Question. Find the number of numbers of 4 digits without repetition formed with the digits 1 2, 3, 4, 5 in which 4 occurs in the thousands place and 5 occurs in the units place.
Answer : 6

Question. (i) How many 2-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, if the digit can be repeated?
(ii) How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
(iii) How many 5-digit number can be formed using the digits 0, 1, 2, 3, and 4 if the digits can be repeated in a number?
Answer : (i) 10 (ii) 108 (iii) 2500

Question. A letter lock consists of three rings, each marked with 10 different letters. In how many ways is it possible to make an unsuccessful attempt to open the lock?
Answer : 999

Question. Ali has 2 school bags, 3 tiffin boxes and 2 water bottles. In how many ways can he carry these items choosing one each.
Answer : 12

Question. Find n, if ^n-1P₃ : ⁿP₄ = 1 : 9 .
Answer : n = 9

Question. How many five digit telephone numbers can be constructed using the digits 0 to 9.
(i) If each number starts with 59, for example 59612 etc., and no digit appears more than once?
(ii) If each number starts with 67 and no digit appears more than once?
Answer : (i) 336 (ii) 336

Question. (i) Given 5 flags of different colours how many different single can be generated if each signal requires the use of 2 flags, one below the other?
(ii) Given 4 flags of different colours, how many different signals can be generated if a signal requires the use of 2 flags one below the other?
(iii) Find the number of different signals that can be generated by arranging at least two flags in order (one below the other) on a vertical staff, if five different flags are available.
Answer : (i) 20 (ii) 12 (iii) 320

Question. (i) How many numbers between 100 and 1000 can be formed with the digits, 1, 2, 3, 4, 5, 6, 7; no digit being repeated?
(ii) How many numbers lying between 100 and 1000 can be formed with the digits 0, 1, 2, 3, 4, 5 if the repetitions of the digits in not allowed?
Answer : 81. (i) 210, (ii) 100

Question. How many numbers each lying between 100 and 1000 can be formed with the digits 2, 3, 4, 0, 8, 9; no digit being repeated?
Answer : 100

Question. Find the total number of ways in which n distinct objects can be put into two different boxes.
Answer : 2ⁿ

Question. A telegraph has 5 arms and each arm can have three distinct positions, including the position of rest. How many signals can be made using the telegraphs?
Answer : 242

Question. Find the number of different signals that can be made by arranging at least 3 flags in order on a vertical pole, if 6 different flags are available.
Answer : 1920

Question. How many three digit numbers are there such that at least one of their digit is 7?
Answer : 252

Question. A team consists of 5 boys and 4 girls. It plays single matches against another team consisting of 6 boys and 3 girls. How many matches can be arranged between the two teams if a boys plays against a boy and a girl plays against a girl?
Answer : 42

Question. Rajeev has 3 pants and 2 shirts. How many different pairs of a pant and a shirt, can he dress up with?
Answer : 6

Question. Find r, if 5. ⁴P_r = 6.⁵P_r-1 .
Answer : r = 3

Question. Ten different letters of an alphabet are given, words with five letters are formed from these given letters. Find the number of words which have at least one letter repeated.
Answer : 10⁵ – ¹⁰P₅

Question. In telegraph communication, the Morse code is used in which all the letters of the English alphabet, digit 0 to 9 and even the punctuation marks, all usualy referred as characters, are represented by ‘dots’ and ‘dashes’.
For example, E is represented by a dot (.), T by a dash (–), O by three dashes (– – –), S by three dots (. . .) and so on. Thus, SOS is represented by (. . . – – – . . .) .
(i) How many characters can be transmitted using one symbol (do or dash), two symbols, three symbols, four symbols? Also find the total number of characters which can be transmitted using at most four symbols.
(ii) How many characters can be transmitted by using (a) exactly five symbols? (b) at most five symbols?
Answer : (i) 30 (ii) (a) 32 (b) 62

Question. If ⁿP₅ = 42. ⁿP₃, n > 4, then find the value of n.
Answer : n = 10

Question. If ⁿP₃ = 9240, find n.
Answer : n = 22

Question. Seven songs are to be rendered in a programme. In how many different orders could they be rendered?
Answer : 5040

Question. Ten horses are running a race. In how many ways can these horses come in the first, second and third place, assuming no ties?
Answer : 720

Question. A person is to walk from A to B. However, he is restricted to walk only to the right of A or upwards of A, but not necessarily in the order. One such path is shown in the figure. Determine the total number of paths available to the person from A to B.

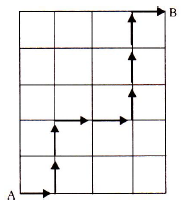
Answer : 126

Question. Find the number of words which can be made using all the letters of the word AGAIN. If these words are written as in a dictionary, what will be the fiftieth word?
Answer : NAAIG

Question. Find the number of words that can be made by arranging the letters of the word ‘INTERMEDIATE’ so that
(i) The relative order of vowels and consonants do not change.
(ii) The order of vowels do not change.
Answer : (i) 6! / 2!3! × 6! / 2!3! = 21600
(ii) 12! / 6!2! = 332640

Question. In how many permutations of the letters of the word ‘PARALLEL’ all the L do not come together.
Answer : 3000